线性回归(linear regression)
假设函数:
????????通常也写为
,假设函数也就是用来预测的函数。
????????称为模型参数,通过选择
两个参数得值来表示假设函数从而合理预测。
????????idea:输入x时预测的值最接近该样本对应的y值时得参数
?最小化问题:通过找出使得预测值与真实值之间的差的平方的相加总和最小
????????m表示训练集样本容量。
代价函数(cost function):顾名思义,付出的代价越小越好
????????因此目标越小越好
例:①只有一个参数时,
????????设,此时假设函数

????????根据上图可看出当时,代价函数
达到最小。则当
时,这条直线是最好的,最符合的,这时的拟合程度最佳。
?②同时拥有两个参数时,

????????通过等高线图来判断,可以把此图想像成一个碗,中心为的最小值,每条线代表的高度都是一样的,即
相同。
梯度下降(gradient descent):用于最小化各种函数

?观察上图,将图形比作山,在山上一步步向下走直到最低点这个过程就是梯度下降法做的事。
步骤:
①给定(通常设
都为0)
②通过不停地一点点改变,来使
变小,直到找到J 的最小值或则局部最小值。
? ? ? ? ? ?(for j=0 and j=1)
?其中:=表示赋值。称为学习率,它控制我们以多大幅度更新参数
。
注意:需要同步更新。
各项意义:
导数项:

学习率:?
????????若太小,每次移动的步伐很小会使迭代次数增多。如下图所示:

????????若太大,会导致无法收敛或者发散。如下图所示:

????????当然学习率并不需要一直改变,根据定义,当达到局部低点时,导数等于0。因此当我们接近局部最低点时,导数值
会自动变得越来越小,所以梯度下降将自动采取较小的幅度,这就是梯度下降的运行方式。
线性回归的梯度下降 (适用于单一的特征量)
????????线性回归的代价函数是一个凸函数的图像,如下图:

????????这种函数没有局部最优解,只有一个全部最优解,。当计算这种代价函数的梯度下降时,只要使用线性回归的梯度下降,最后只获得一个全部最优解
????????将假设函数与代价函数相结合,可得出下列式子?:
?
此方法也称为Batch Gradient Descent,每一步的梯度下降都遍历了整个训练集的样本。但这个方法当样本数目很多时,训练过程会很慢。
多元线性回归
? ? ? ? 符号说明:
? ? ? ? ? ? ? ? n:特征量的数目;
????????????????:第i个训练样本中第j个特征量的值。
? ? ? ? 假设函数:
设,则该假设函数可写为:
????????若了解线性代数,则可知等于向量的内积,即
。此时特征向量x是从0开始标记的n+1维的向量。
多元梯度下降法

多元梯度下降法技巧?
特征缩放
????????当不同特征值都处在一个相近的范围内,这样梯度下降法收敛更快。
? ? ? ? 执行特征缩放的目的是将特征值的取值约束在,当然也并不是说取值一定要严格限制在这个范围内,如下所示:

?学习率
????????①画图

?????????②自动收敛测试
????????若代价函数迭代后的下降低于一个很小的值
,这个测试则判断函数已收敛
但是选择一个合适的是很难的,但通过画图还可以发现算法是否正常工作。
a. 若所画图如下所示:

出现这种图像一般是因为一开始选择了较大的学习率,因此在尝试最小化函数时,梯度下降法直接越过了最小值,如下图

?因此我们需要选择一个较小的学习率?。
b.?

?出现这种情况也选择较小的学习率。
总结:
① 学习率过小时会出现收敛缓慢的问题;
② 学习率过大时,可能出现收敛缓慢,代价函数
不能保证每次迭代都下降,甚至可能不收敛。
正规方程法normal equation(区别于迭代方法的直接解法)
m:训练样本数;n:特征变量数
利用正规方程求解课直接一步得到的最优值。
一般我们会多设一列,因此设计矩阵X为m*(n+1)维的矩阵,y是m维向量

?用即可求出使代价函数
最小的
值。
梯度下降法与正规方程组的比较
梯度下降法 :
????????① 需要选择学习率;
????????② 需要多次迭代;
????????③ 当特征变量很多时仍能很好的工作。
正规方程组:
? ? ? ??① 不需要选择学习率;
????????② 不需要多次迭代;
????????③ 当特征变量很多时不能很好的工作,因为要计算,计算量过大,时间消耗比梯度下降法长。一般认为特征变量数多于10000时考虑使用梯度下降法。
当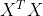 不可逆时,一般有以下两种情况:
不可逆时,一般有以下两种情况:
? ? ? ? ① 多余特征。如呈线性关系,则保留其中一个便可;
? ? ? ? ② 太多特征量。当m<n时,比如m=10,n=100,这显然是不合理的,可以选择删除一些无关紧要的特征量或将其正则划。