【系列说明】
本系列用于复习与回顾机器学习的方法,总结算法流程,适当剖析源代码,列出适合算法的数据集,以及重要的调参参数。
案例1-中心漂移聚类(MeanShift)方法
数据集内容:
(1)numpy生成数据集,平面数据集,即二维向量,用矩阵 A(2*10000)表示
(2)设立三个数据的中心点 centers,分别为(1, 1), (-1, -1), (1, -1)
(3)每一类中数据点的标准差cluster_std 为0.6时,恰好(有数据粘合)能够区分这些类
(4)设置带宽,函数用作于mean-shift算法估计带宽,如果MeanShift函数没有传入bandwidth参 数,MeanShift会自动运行estimate_bandwidth 函数说明如下 :
def estimate_bandwidth(X, quantile=0.3, n_samples=None, random_state=0,
n_jobs=1):
"""Estimate the bandwidth to use with the mean-shift algorithm.
That this function takes time at least quadratic in n_samples. For large
datasets, it's wise to set that parameter to a small value.
Parameters
----------
X : array-like, shape=[n_samples, n_features]
Input points.
quantile : float, default 0.3
should be between [0, 1]
0.5 means that the median of all pairwise distances is used.
n_samples : int, optional
The number of samples to use. If not given, all samples are used.
random_state : int or RandomState
Pseudo-random number generator state used for random sampling.
n_jobs : int, optional (default = 1)
The number of parallel jobs to run for neighbors search.
If ``-1``, then the number of jobs is set to the number of CPU cores.
Returns
-------
bandwidth : float
The bandwidth parameter.
"""
#根据random_state生成伪随机数生成器
random_state = check_random_state(random_state)
if n_samples is not None:
#permutation将序列打乱 并取n_samples个数的样本
idx = random_state.permutation(X.shape[0])[:n_samples]
X = X[idx]
#非监督方式进行近邻搜索
#quantile的值表示进行近邻搜索时候的近邻占样本的比例
nbrs = NearestNeighbors(n_neighbors=int(X.shape[0] * quantile),
n_jobs=n_jobs)
nbrs.fit(X)
bandwidth = 0.
#gen_batches(n,batch_size) 根据batch_size的大小生成0~n的切片
for batch in gen_batches(len(X), 500):
#kneighbors返回batch里面每个点的n_sample个邻居的距离(不包括自己)
#n_sample要是没有定义那就和NearestNeighbors里面的n_neighbors相等
#还有个返回值是下标,不过用不到就拿_忽略了
d, _ = nbrs.kneighbors(X[batch, :], return_distance=True)
#将每个点的最近的n_neighbors个邻居中最远的距离加起来
bandwidth += np.max(d, axis=1).sum()
#本质上就是求平均最远k近邻距离
return bandwidth / X.shape[0]
参数quantile 在计算近邻的时候会挑选最近的(样本总数*quantile)个样本计算样本的欧式距离,这个参数的与样本X的分布关系很大,本案例的数据集用make_blobs方法生成提前设置了三个中心点,而后设定标准差,来使数据点满足从中心点密集的各向同性高斯blobs,即数据集总体满足正态分布,若将中心点间距设置的较远,标准差值足够小,就会出现如下图的分布:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4NcllOyQ-1642345349633)(C:\Users\YangShi\AppData\Roaming\Typora\typora-user-images\image-20220105213912078.png)]
? 可以严格被划分,真实案例数据中,几乎没有数据不经过分层、滤波处理,可以有如此好的表现,但也给我们启发,我们可以将数据细分,在某一个小数据集中达到如此效果,再将多个小数据集结果进行划分。
(5)中心漂移理论详解:
? 给定d维空间的n个数据点集X,那么对于空间中的任意点x的mean shift向量基本形式可以表示为:
M
h
=
1
/
k
∑
(
x
i
?
x
)
Mh = 1/k ∑(xi - x)
Mh=1/k∑(xi?x)
? 这个向量就是漂移向量,其中Sk表示的是数据集的点到x的距离小于球半径h的数据点。而漂移的过程,说的简单一点,就是通过计算得漂移向量,然后把球圆心x的位置更新一下,更新公式为:
x
=
x
+
m
k
x = x + mk
x=x+mk
? 使得圆心的位置一直处于力的平衡位置。
? 总结为一句话就是:求解一个向量,使得圆心一直往数据集密度最大的方向移动。说的再简单一点,就是每次迭代的时候,都是找到圆里面点的平均位置作为新的圆心位置。
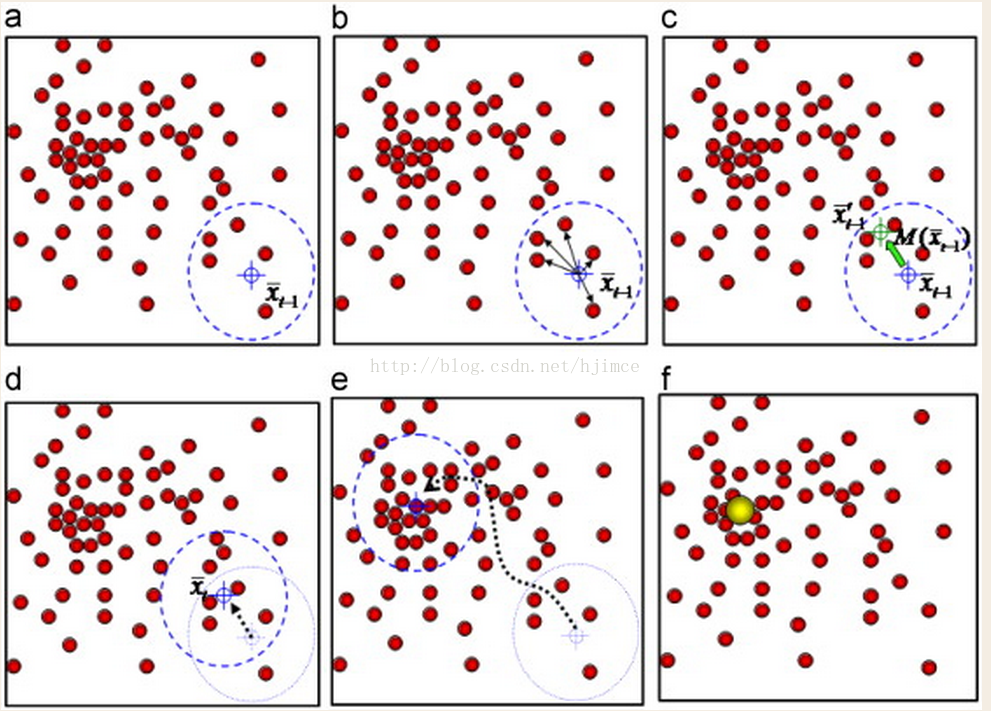
? 假设在一个多维空间中有很多数据点需要进行聚类,Mean Shift的过程如下:
? (5.1)、在未被标记的数据点中随机选择一个点作为中心center, 本案例的取三个确定的中心点;
? (5.2)、找出离center距离在bandwidth之内的所有点(get_bin_seeds),记做集合M,认为这些点属于簇c。同时,把这些求内点属于这 个类的概率加1,这个参数将用于最后步骤的分类;
? (5.3)、以center为中心点,计算从center开始到集合M中每个元素的向量,将这些向量相加,得到向量shift。
? (5.4)、center = center+shift,即center沿着shift的方向移动,移动距离是||shift||。
? (5.5)、重复步骤2、3、4,直到shift的大小很小(就是迭代到收敛),记住此时的center。注意,这个迭代过程中遇到的点都应该归类到簇c。
? (5.6)、如果收敛时当前簇c的center与其它已经存在的簇c2中心的距离小于阈值,那么把c2和c合并。否则,把c作为新的聚类,增加1类(并查集算法)。
? (5.7)、重复1、2、3、4、5直到所有的点都被标记访问。
? (5.8)、分类:根据每个类,对每个点的访问频率,取访问频率最大的那个类,作为当前点集的所属类。
? 简单的说,mean shift就是沿着密度上升的方向寻找同属一个簇的数据点。
案例小结:
? 本案例的数据是寻找了三个中心,由中心向外模拟高斯分布的,换言之,后面的中心漂移的算法,最终的良好的结果,一定是向预定中心靠近;也就是说,在做中心漂移聚类分析的时候需要原始数据集满足高斯分布(是否zero-mean需要真实数据验证,理论上不需要)
引用博客如下:
[1] http://blog.csdn.net/hjimce/article/details/45718593
[2] https://blog.csdn.net/jiaqiangbandongg/article/details/53495419