【写在前面】
今天公司有个刚毕业学生一直问深度学习的CNN网络模型相关的问题,LetNet-5虽然简单,但是包含了深度学习CNN模型的基本组成模块,包含(卷积、池化、全连接等结构)为了帮助理解拿了一个最简单的LetNet网络做一个知识梳理帮助理解。
(阅读本文章之前具体的卷积、池化原理大家已经深入理解)
权值共享
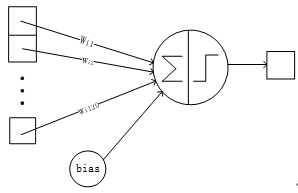
图像识别的领域同时网络的类型是基于BP的,因此针对这个领域先看看BP的缺点,我们知道BP网络是全连接的,对于图片的识别,我们不用提取特征,一般一层提取特征的效果并不是很好,因此我们需要很多层,如果按照BP进行全连接,会使得权值数量急剧增加,想要训练这么多的权值,样本必须足够的才行,即使样本数量够,但是计算量也会急剧增加,而且还有面临梯度消失的情况,因此需要改进连接的方式即采用局部连接和权值共享,如下图:
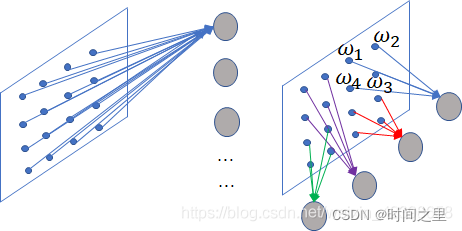
假如一张图片的像素点为4x4的,上图的左边图W为全连接,一个神经元就有16个连接 ,每个连接的权值不同,因此如果有n个神经元则有16n个权值,左图就是局部连接,此时加入四个像素点连接一个神经元,则需要四个,但是如果像素很多的情况下,权值还是很多,此时是按照每个神经元的连接权值如上图的是其中一个神经元的是4个权值,所谓权值共享,就是其他神经元的权值也使用这四个值,此时的位置和数值都是这样对应的,这里大家需要理解。即四个神经元只有四个不同的权值,现在我们来算算,按照右边的计算:
全连接的权值数:4x4x4=64(前面两是像素点,后面的4是神经元,这里先不考虑偏置值) ,
局部连接的权值:4x4=16(4个神经元,每个神经元4个权值)
局部连接和权值共享: 4
因此权值的数量就降低了,这就是通过局部连接和权值共享来解决BP的存在的问题,这里的理论依据就是根据上面说的感受野进行简化的,但是按照上图的局部连接存在一个问题就是边缘过度不平滑,会出现边缘效应,为了解决这个问题引入了采样窗口法使其彼此重叠,因为这样做和卷积很类似,因此采样窗口就称为卷积核了,我们看这个窗口是怎么重叠的;假如采样窗口为3x3,所谓重叠,我们每次左移一个像素点送给神经元,往下移动时也是这样的,这样就避免了边缘效应了具体效果如下图所示;
卷积原理
简要图示:
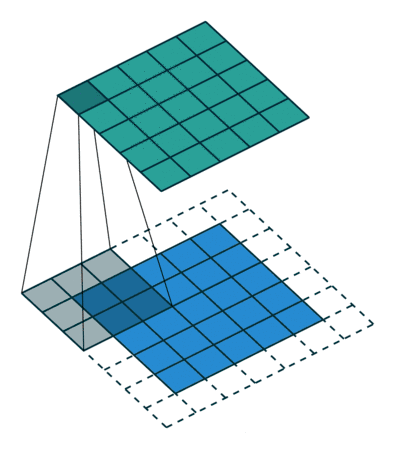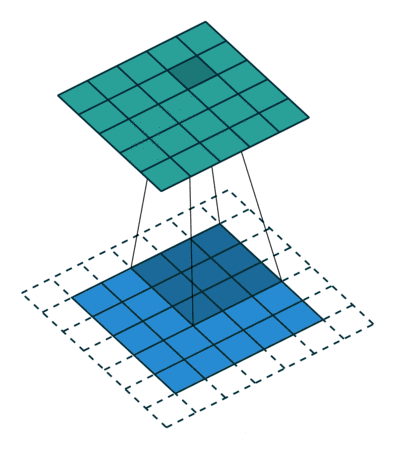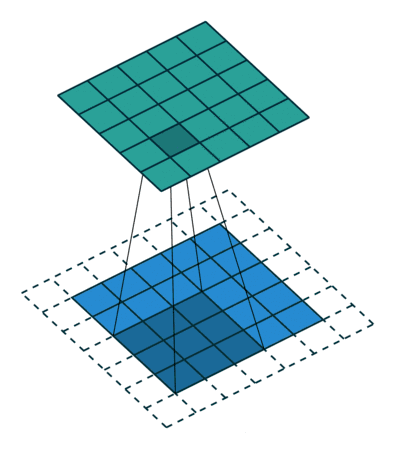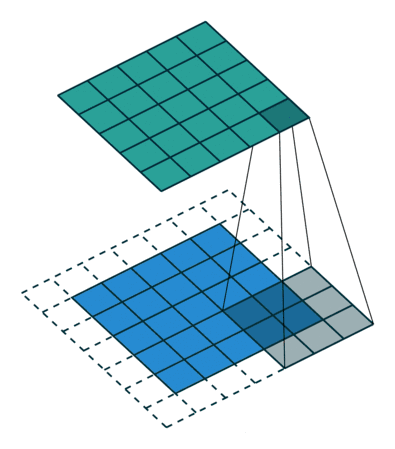
池化原理
简要图示:
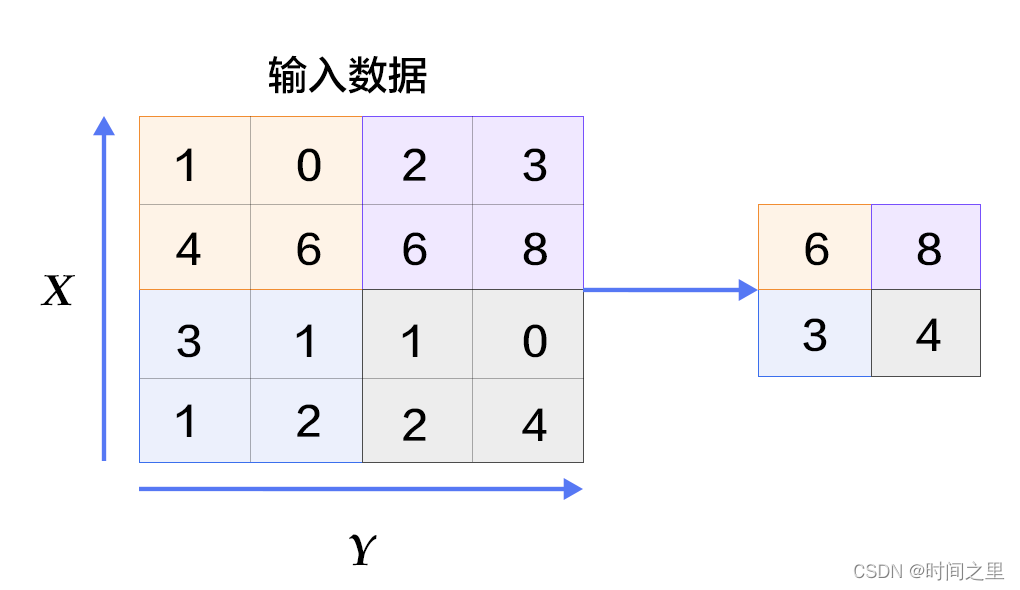
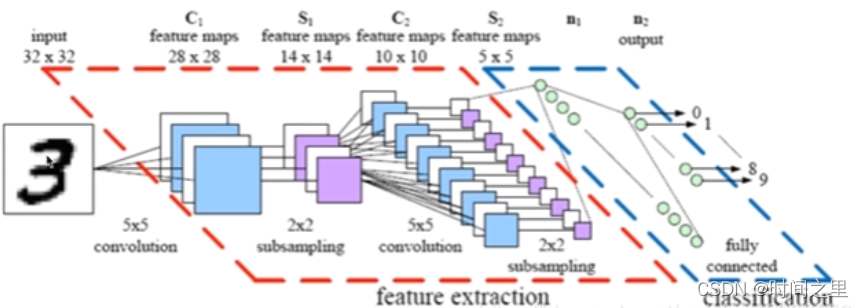
【LetNet介绍】
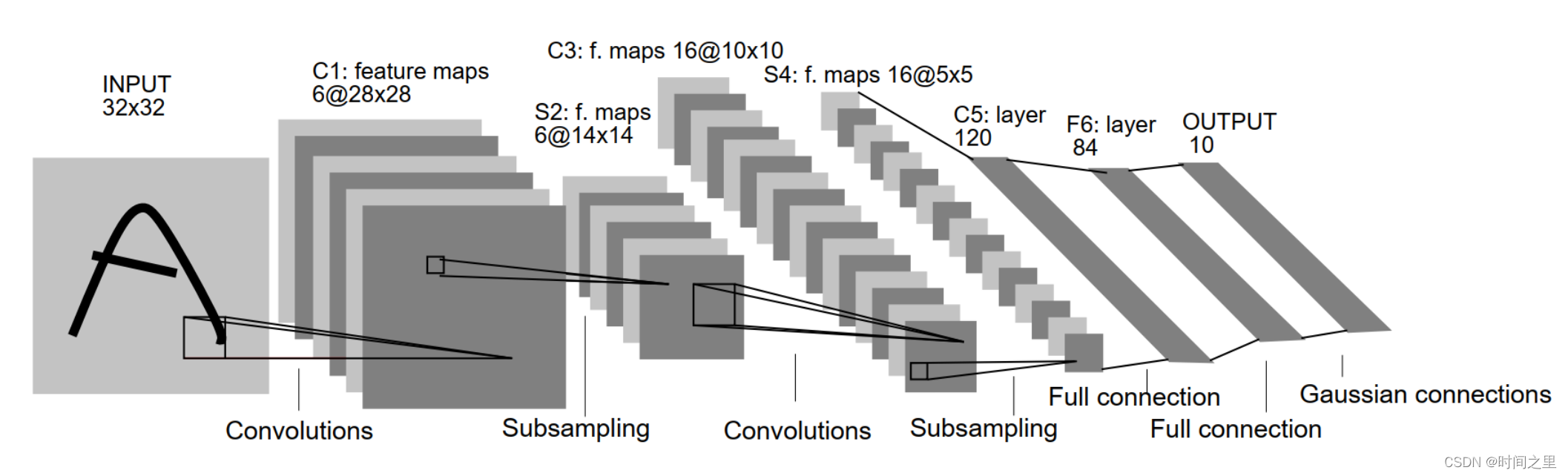
LetNet实现过程如上图所示:
含输入层总共8层网络,分别为:
输入层(INPUT)、
卷积层(Convolutions,C1)、
池化层(Subsampling,S2)、
卷积层(C3)、
池化层(Subsampling,S4)、
卷积层(C5)、
全连接层(F6)、
输出层(径向基层)
论文原文
论文原文:
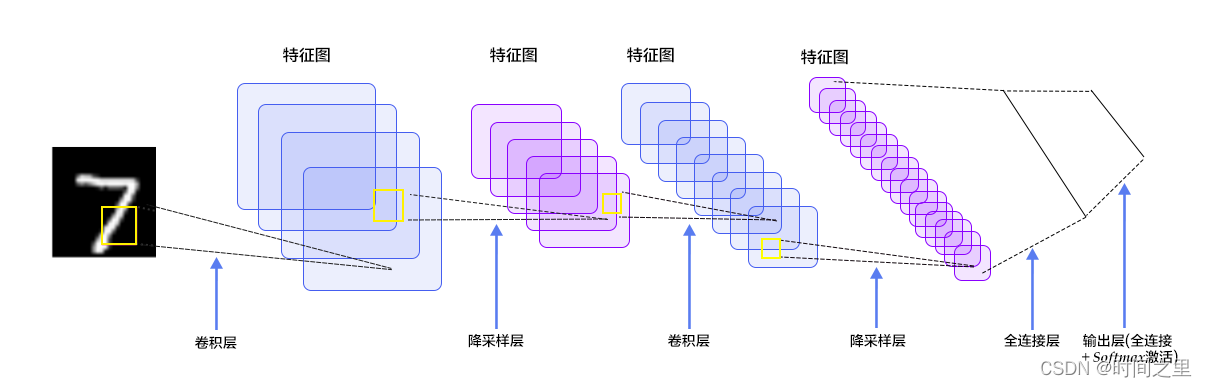
输入的二维图像,先经过两次卷积层到池化层,再经过全连接层,最后使用softmax分类作为输出层。大致过程如下图所示:
实现过程参数变化概览
分为以下几步:
1.INPUT层-输入层:(输入32x32大小的图像)
2.C1层-卷积层
3.S2层-池化层(下采样层)
4.C3层-卷积层
5.S4层-池化层(下采样层)
6.C5层-卷积层
7.F6层-全连接层
8.Output层-全连接层
整个过程对应参数理解如下表所示:
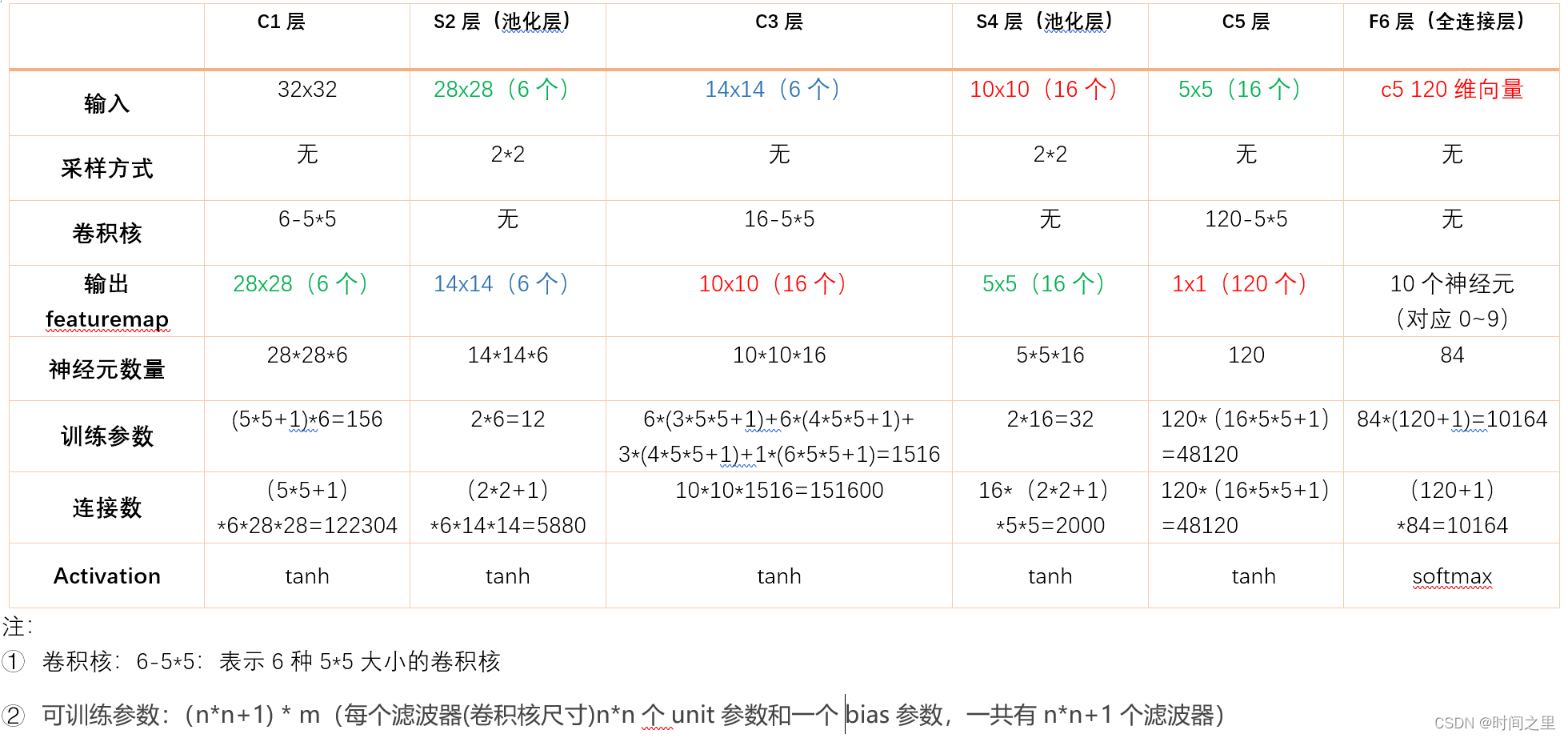
详细过程
1.INPUT层-输入层:(输入32x32大小的图像)
数据输入 INPUT 输入图像的尺寸归一化为32*32
2.C1层-卷积层
输入图片:3232
卷积核大小:55
卷积核种类:6
输出featuremap大小:2828 (32-5+1)=28
神经元数量:28286
可训练参数:(55+1) * 6(每个滤波器55=25个unit参数和一个bias参数,一共6个滤波器)
连接数:(55+1)628*28=122304
详细说明:对输入图像进行第一次卷积运算(使用 6 个大小为 55 的卷积核),得到6个C1特征图(6个大小为2828的 feature maps, 32-5+1=28)。我们再来看看需要多少个参数,卷积核的大小为55,总共就有6(55+1)=156个参数,其中+1是表示一个核有一个bias。对于卷积层C1,C1内的每个像素都与输入图像中的55个像素和1个bias有连接,所以总共有1562828=122304个连接(connection)。有122304个连接,但是我们只需要学习156个参数,主要是通过权值共享实现的。
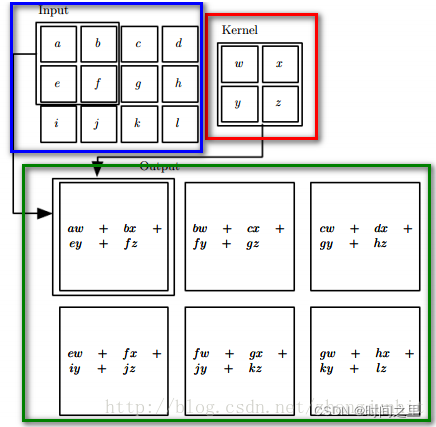
上图表示CNN中卷积操作。对卷积的要点解释:
(1)红色框内为22卷积核。
(2)蓝色框内为34的输入图像。
(3)绿色框为3*3的特征图。
注意:绿框中未包含偏置项。如加入偏置项则每个输出多加上同一个偏置B,此时类似如:aw+bx+ey+fz+B bw+cx+fy+gz+B等。所谓的权值共享是每个卷积运算使用同一个卷积核,在上图中使用的是同一个卷积核,即共享权值。
卷积的优势:
(1) sparse interactions (2) parameter sharing (3) equivariant respections
sparse interactions:
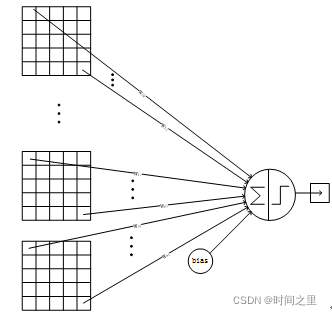
下图是效果图。蓝色框中是全连接神经网络,红色框是卷积网络。
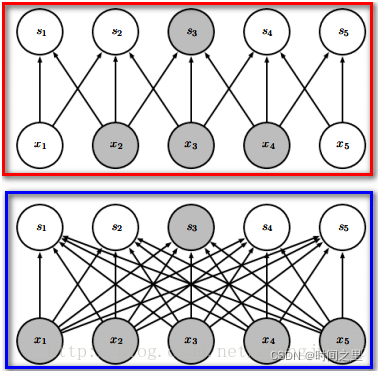
卷积相对于全连接是稀疏的。
优势:1、参数更少 2、计算量降低。那么会不会导致提取的特征丢失了?
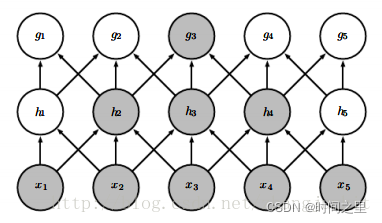
上图是多层结构的联系图,所以可以通过增加网络层数,保留全局的特征。
parameter sharing: 在上面已经分析完毕。优势:同样是减少了参数量。
equivariant respections: 当输入图像通过平移后,卷积的结果也会平移。
原文链接:https://blog.csdn.net/zhangjunhit/article/details/53536915
3.S2层-池化层(下采样层)
输入:2828
采样区域:22
采样方式:4个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过sigmoid
采样种类:6
输出featureMap大小:1414(28/2)
神经元数量:14146
连接数:(22+1)614*14
S2中每个特征图的大小是C1中特征图大小的1/4。
详细说明:第一次卷积之后紧接着就是池化运算,使用 22核 进行池化,于是得到了S2,6个1414的 特征图(28/2=14)。S2这个pooling层是对C1中的2*2区域内的像素求和乘以一个权值系数再加上一个偏置,然后将这个结果再做一次映射。同时有5x14x14x6=5880个连接。
4.C3层-卷积层
输入:S2中所有6个或者几个特征map组合
卷积核大小:55
卷积核种类:16
输出featureMap大小:1010 (14-5+1)=10
C3中的每个特征map是连接到S2中的所有6个或者几个特征map的,表示本层的特征map是上一层提取到的特征map的不同组合
存在的一个方式是:C3的前6个特征图以S2中3个相邻的特征图子集为输入。接下来6个特征图以S2中4个相邻特征图子集为输入。然后的3个以不相邻的4个特征图子集为输入。最后一个将S2中所有特征图为输入。
则:可训练参数:6*(355+1)+6*(455+1)+3*(455+1)+1*(655+1)=1516
连接数:10101516=151600
详细说明:第一次池化之后是第二次卷积,第二次卷积的输出是C3,16个10x10的特征图,卷积核大小是 55. 我们知道S2 有6个 1414 的特征图,怎么从6 个特征图得到 16个特征图了? 这里是通过对S2 的特征图特殊组合计算得到的16个特征图。具体如下:
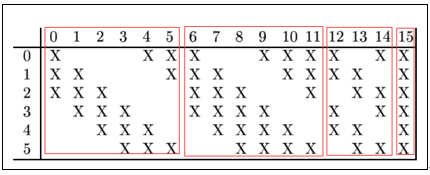
C3的前6个feature map(对应上图第一个红框的6列)与S2层相连的3个feature map相连接(上图第一个红框)
后面6个feature map与S2层相连的4个feature map相连接(上图第二个红框),
后面3个feature map与S2层部分不相连的4个feature map相连接,
最后一个与S2层的所有feature map相连。
卷积核大小依然为55,所以总共有6(355+1)+6*(455+1)+3*(455+1)+1*(655+1)=1516个参数。而图像大小为1010,所以共有151600个连接。
C3与S2中前3个图相连的卷积结构如下图所示:
上图对应的参数为 355+1,一共进行6次卷积得到6个特征图,所以有6(355+1)参数。 为什么采用上述这样的组合了?论文中说有两个原因:1)减少参数,2)这种不对称的组合连接的方式有利于提取多种组合特征。
5.S4层-池化层(下采样层)
输入:1010
采样区域:22
采样方式:4个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过sigmoid
采样种类:16
输出featureMap大小:55(10/2)
神经元数量:5516=400
连接数:16(22+1)55=2000
S4中每个特征图的大小是C3中特征图大小的1/4
详细说明:S4是pooling层,窗口大小仍然是22,共计16个feature map,C3层的16个10x10的图分别进行以2x2为单位的池化得到16个5x5的特征图。有5x5x5x16=2000个连接。连接的方式与S2层类似。
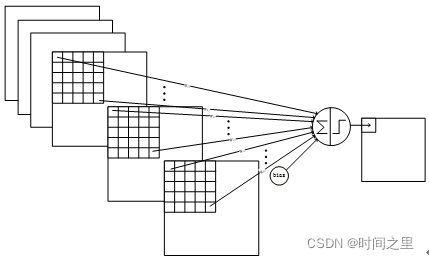
6.C5层-卷积层
输入:S4层的全部16个单元特征map(与s4全相连)
卷积核大小:55
卷积核种类:120
输出featureMap大小:11(5-5+1)
可训练参数/连接:120*(1655+1)=48120
详细说明:这一层还是卷积层,且这一层的特征平面有120个,每个特征平面是5x5的,而上一层的池化层S2只有16个平面且每个平面为5x5,本层使用的卷积核为5x5,因此和池化层正好匹配,那么怎么连接呢?很简单就是这里每个特征平面连接池化层的所有的采样层。这里称呼特征平面已经不合适了,因为每个卷积核只对应一个神经元了,因此本层只有120个神经元并列排列,每个神经元连接池化层的所有层。C5层的每个神经元的连接数为5x5x16+1,因此总共的连接数为:(5x5x16+1)x120=48120,而这一层的权值和连接数一样,因此也有48120个待训练权值。
C5层的网络结构如下:
7.F6层-全连接层
输入:c5 120维向量
计算方式:计算输入向量和权重向量之间的点积,再加上一个偏置,结果通过sigmoid函数输出。
可训练参数:84*(120+1)=10164
详细说明:6层是全连接层。F6层有84个节点,对应于一个7x12的比特图,-1表示白色,1表示黑色,这样每个符号的比特图的黑白色就对应于一个编码。该层的训练参数和连接数是(120 + 1)x84=10164。ASCII编码图如下:

F6层的连接方式如下:
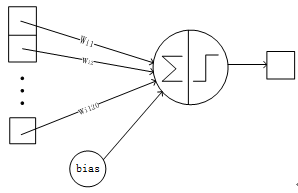
8.Output层-全连接层
Output层也是全连接层,共有10个节点,分别代表数字0到9,且如果节点i的值为0,则网络识别的结果是数字i。采用的是径向基函数(RBF)的网络连接方式。
本层的输出有激活函数,激活函数为双曲正切函数:
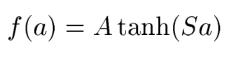
根据论文解释:A的幅值,S是原点处的倾斜率,A的经验值是1.7159,原因没说。
下面我们看看他是和F6层是如何连接的,他不在是BP的神经输出层,而是基于径向基神经网络的输出层,这里使用的是更简单的欧几里得径向基函数,如下:
假设x是上一层的输入,y是RBF的输出,则RBF输出的计算方式是:
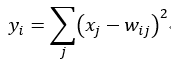
上式w_ij 的值由i的比特图编码确定,i从0到9,j取值从0到7*12-1。
公式含义:
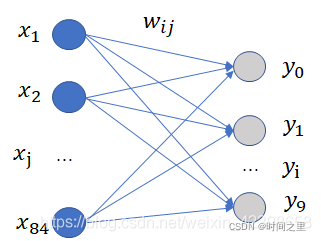
径向基神经网络,他基于距离进行衡量两个数据的相近程度的,RBF网最显著的特点是隐节点采用输人模式与中心向量的距离(如欧氏距离)作为函数的自变量,并使用径向基函数(如函数)作为激活函数。径向基函数关于N维空间的一个中心点具有径向对称性,而且神经元的输人离该中心点越远,神经元的激活程度就越低。
上式是基于欧几里得距离,就是说F6层为84个输入用表示,而输出有10个用表示,而权值使用,上式说明所有输入和权值的距离平方和为依据判断,如果越相近距离越小,输出越小则去哪个,如果我们存储的到的值为标准的输出,如标准的手写体0,1,2,3等,那么最后一层就说明。F6层和标准的作比较,和标准的那个图形越相似就说明就越是那个字符的可能性更大。
RBF输出的值越接近于0,则越接近于i,即越接近于i的ASCII编码图,表示当前网络输入的识别结果是字符i。该层有84x10=840个参数和连接。
这里标准的每个字符都是像素都是12x7=84.这就是解释了为什么F6层的神经元为84个,因为他要把所有像素点和标准的比较在进行判断,因此从这里也可以看出,这里不仅仅可以训练手写体数字,也可以识别其他字符,取决于和网络的设计,这些可以认为修改的。例如我们让他识别可打印的ASCII码,把小图片添加到这里就可以了,同时增加输出的神经元个数就可以完成了。再给出另外一个详细的图:
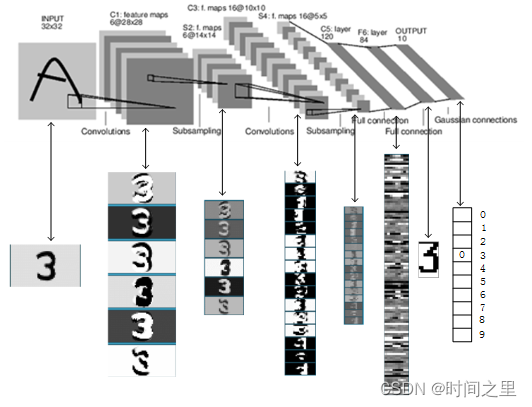
LeNet-5识别数字3的过程如下图所示:
【参考链接】
网络解析(一):LeNet-5详解
LeNet-5
深度学习 — 卷积神经网络CNN(LeNet-5网络详解)
论文笔记