简单介绍线性代数中的基本数学对象、算术和运算,并用数学符号和相应的代码实现来表示它们。(pytorch)
1.1 标量
标量由只有一个元素的张量表示。
例:实例化两个标量,并执行一些熟悉的算术运算,即加法、乘法、除法和指数。
import torch
x = torch.tensor(3.0)
y = torch.tensor(2.0)
x + y, x * y, x / y, x**y
输出:
(tensor(5.), tensor(6.), tensor(1.5000), tensor(9.))
1.2 向量
可以将向量视为标量值组成的列表。 我
们将这些标量值称为向量的元素(element)或分量(component)。
例:
x = torch.arange(4)
x
输出:
tensor([0, 1, 2, 3])
我们可以使用下标来引用向量的任一元素。 例如,我们可以通过 x[i] 来引用第 i 个元素。
x[3]
输出:
tensor(3)
向量只是一个数字数组,就像每个数组都有一个长度一样,每个向量也是如此。
与普通的Python数组一样,我们可以通过调用Python的内置len()函数来访问张量的长度。
len(x)
输出:
4
当用张量表示一个向量(只有一个轴)时,我们也可以通过.shape属性访问向量的长度。 形状(shape)是一个元素组,列出了张量沿每个轴的长度(维数)。 对于只有一个轴的张量,形状只有一个元素。
x.shape
输出:
torch.Size([4])
请注意,维度(dimension)这个词在不同上下文时往往会有不同的含义,这经常会使人感到困惑。 为了清楚起见,我们在此明确一下: 向量或轴的维度被用来表示向量或轴的长度,即向量或轴的元素数量。 然而,张量的维度用来表示张量具有的轴数。 在这个意义上,张量的某个轴的维数就是这个轴的长度。
1.3 矩阵
正如向量将标量从零阶推广到一阶,矩阵将向量从一阶推广到二阶。 在代码中表示为具有两个轴的张量。
当调用函数来实例化张量时, 我们可以通过指定两个分量 m 和 n 来创建一个形状为 m×n 的矩阵。
A = torch.arange(20).reshape(5, 4)
A
输出:
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
矩阵的转置:
A.T
输出:
tensor([[ 0, 4, 8, 12, 16],
[ 1, 5, 9, 13, 17],
[ 2, 6, 10, 14, 18],
[ 3, 7, 11, 15, 19]])
定义一个矩阵:
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
输出:
tensor([[1, 2, 3],
[2, 0, 4],
[3, 4, 5]])
矩阵的比较:
只能是具有相同形状的矩阵
将B与它的转置进行比较:
B == B.T
输出:
tensor([[True, True, True],
[True, True, True],
[True, True, True]])
1.4 张量
就像向量是标量的推广,矩阵是向量的推广一样,我们可以构建具有更多轴的数据结构。
张量为我们提供了描述具有任意数量轴的 n 维数组的通用方法。 例如,向量是一阶张量,矩阵是二阶张量。
当我们开始处理图像时,张量将变得更加重要,图像以 n 维数组形式出现, 其中3个轴对应于高度、宽度,以及一个通道(channel)轴, 用于表示颜色通道(红色、绿色和蓝色)。
X = torch.arange(24).reshape(2, 3, 4)
X
输出:
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
给定具有相同形状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量。 例如,将两个相同形状的矩阵相加,会在这两个矩阵上执行元素加法。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存,将A的一个副本分配给B
A, A + B,A * B
输出:
(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]]),
tensor([[ 0., 2., 4., 6.],
[ 8., 10., 12., 14.],
[16., 18., 20., 22.],
[24., 26., 28., 30.],
[32., 34., 36., 38.]]),
tensor([[ 0., 1., 4., 9.],
[ 16., 25., 36., 49.],
[ 64., 81., 100., 121.],
[144., 169., 196., 225.],
[256., 289., 324., 361.]]))
将张量乘以或加上一个标量不会改变张量的形状,其中张量的每个元素都将与标量相加或相乘。
a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape
输出:
(tensor([[[ 2, 3, 4, 5],
[ 6, 7, 8, 9],
[10, 11, 12, 13]],
[[14, 15, 16, 17],
[18, 19, 20, 21],
[22, 23, 24, 25]]]),
torch.Size([2, 3, 4]))
1.5 点积
相同位置的按元素乘积的和,点积可以表示加权平均(weighted average)
x = torch.arange(4,dtype = torch.float32)
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)
输出:
(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))
1.6 矩阵乘法
例:
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = torch.ones(4, 3)
A,B,torch.mm(A, B)
输出:
(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]]),
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]]),
tensor([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]]))
我们在A和B上执行矩阵乘法。 这里的A是一个5行4列的矩阵,B是一个4行3列的矩阵。 两者相乘后,我们得到了一个5行3列的矩阵。
1.7 范数
线性代数中最有用的一些运算符是范数(norm)。 非正式地说,一个向量的范数告诉我们一个向量有多大。 这里考虑的大小(size)概念不涉及维度,而是分量的大小。
给定任意向量 x ,向量范数要满足一些属性。
-
一个性质是:如果我们按常数因子 α 缩放向量的所有元素, 其范数也会按相同常数因子的绝对值缩放:
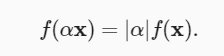
-
第二个性质是我们熟悉的三角不等式
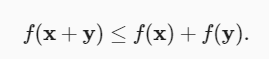
-
第三个性质简单地说范数必须是非负的
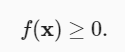
L2 范数:
欧几里得距离是一个 L2 范数
假设 n 维向量 x 中的元素是 x1,…,xn ,其 L2 范数是向量元素平方和的平方根:
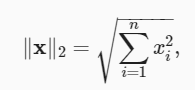
其中,在 L2 范数中常常省略下标 2 ,也就是说 ∥x∥ 等同于 ∥x∥2 。 在代码中,我们可以按如下方式计算向量的 L2 范数。在深度学习中,我们更经常地使用 L2 范数的平方。
u = torch.tensor([3.0, -4.0])
torch.norm(u)
输出:
tensor(5.)
L1 范数:
表示为向量元素的绝对值之和:
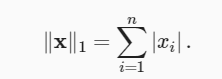
与 L2 范数相比, L1 范数受异常值的影响较小。 为了计算 L1 范数,我们将绝对值函数和按元素求和组合起来。
torch.abs(u).sum()
输出:
tensor(7.)
L2 范数和L1范数都是更一般的Lp范数的特例:
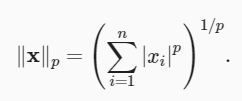
在深度学习中,我们经常试图解决优化问题: 最大化分配给观测数据的概率; 最小化预测和真实观测之间的距离。 用向量表示物品(如单词、产品或新闻文章),以便最小化相似项目之间的距离,最大化不同项目之间的距离。 目标,或许是深度学习算法最重要的组成部分(除了数据),通常被表达为范数。