《机器学习》——第二章 模型评估与选择
一、经验误差和过拟合
1.1 经验误差和泛化误差
错误率公式
错误率
=
错误样本
样本总数
\text{错误率}=\frac{\text{错误样本}}{\text{样本总数}}
错误率=样本总数错误样本?
精度公式
精度
=
1
?
错误率
\text{精度}=1-\text{错误率}
精度=1?错误率
经验误差(训练误差):学习器在训练集上的误差
泛化误差:学习器在新样本集上的误差
1.2 过拟合和欠拟合
过拟合:学习器把训练集的样本学得太好了,可能把训练样本自身的一些特点当做了潜在样本都会具有一般的性质,导致泛化能力下降
欠拟合:对训练样本的一般性质尚未学好
周志华老师在书中举出了这样的一个例子

二、评估方法
由于泛化误差难以测试出,因此采用测试误差作为近似误差即
泛化误差
≈
测试误差
\text{泛化误差}\approx \text{测试误差}
泛化误差≈测试误差
2.1 留出法
直接将数据集D划分为两个互斥的集合,其中一个是训练集S,一个是测试集T,S和T满足下列关系
{
D
=
S
∪
T
?
=
S
∩
T
\left\{ \begin{array}{c} D=S\cup T\\ \varnothing =S\cap T\\\end{array} \right.
{D=S∪T?=S∩T?
Tip:由于数据样本容量的大小不同,对最终模型学习的结果产生一定的影响,而因为学习算法需要对数据集D进行学习,而这种方法需要对数据集D进行划分,因此通用的解法是将大概2/3~4/5的数据作为训练集,剩下来的作为测试集
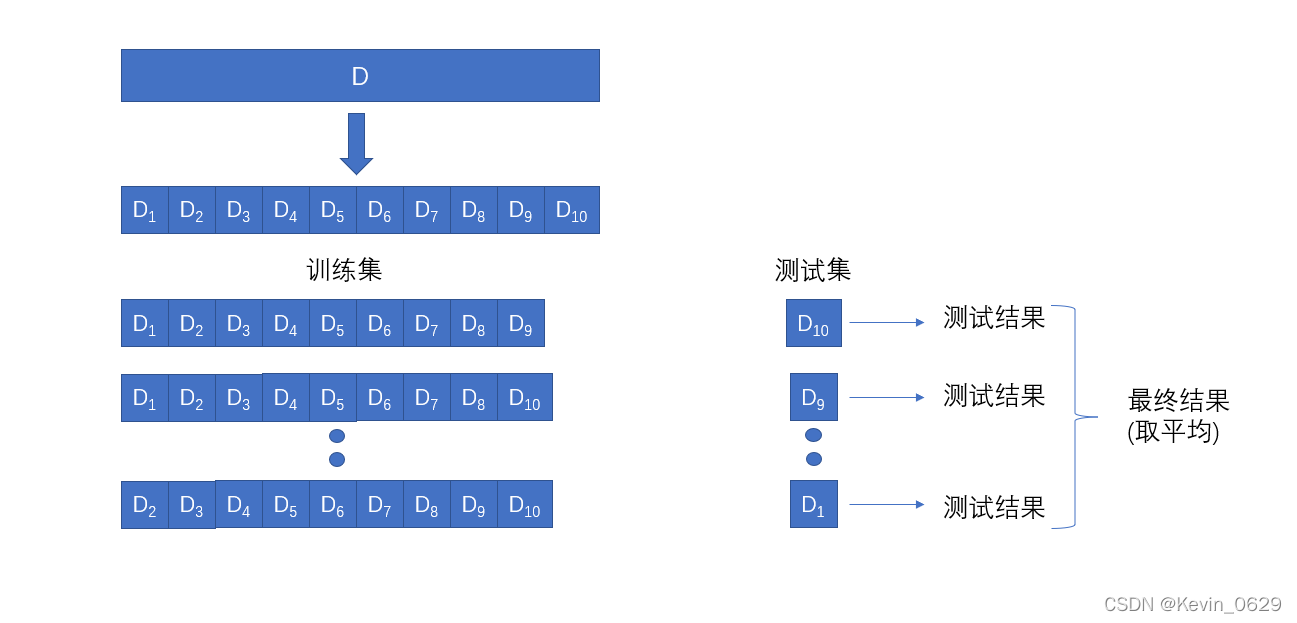
2.2 交叉验证法
交叉验证法:对数据集D划分为K个大小相似的互斥子集,采用分层采样的方法,即
D
=
D
1
∪
D
2
∪
?
∪
D
k
(
D
i
≠
D
j
)
D=D_1\cup D_2\cup \cdots \cup D_k\left( D_i\ne D_j \right)
D=D1?∪D2?∪?∪Dk?(Di??=Dj?)
交叉验证法的流程图如下所示,
2.3 自助法
一句话概括就是,通过自助的方法对数据集中的数据进行等概率的放回型采用,所以样本在m次采样中始终不被采样到的概率为
lim
?
(
1
?
1
m
)
m
≈
0.38
\lim \left( 1-\frac{1}{m} \right) ^m\approx 0.38
lim(1?m1?)m≈0.38
2.4 调参与最终模型
每一个模型都会设定一个默认的default值参数,但是往往这个default值可能训练出来的模型的效果不好,因此就需要对所使用的算法进行调参,对算法进行调参就涉及到大量的运算,因此现在常用的方法有设定一个参数的范围和步长,通过对参数的调节,然后去训练模型,但是因此算法中的参数有很多个,不止有一个参数,因此仍然存在一定的计算量,同时现在比较新的有网格搜索法等调参方法,只用通过对模型的参数进行调节后,这个模型才能在这种问题上表现出很好的能力
三、性能度量
怎么样才能对学习器,对算法做出一个评估,到底这个算法这个学习器是好的,这个算法是好的呢,这就需要用到性能度量的一些常用的方法
3.1 错误率与精度
针对于二分类的问题
错误率:错误率是分类错误的样本占样本总数的比例,定义如下
E
(
f
;
D
)
=
∫
I
I
(
f
(
x
)
≠
y
)
p
(
x
)
d
x
E\left( f;D \right) =\int{II\left( f\left( x \right) \ne y \right)}p\left( x \right) dx
E(f;D)=∫II(f(x)?=y)p(x)dx
精度:精度是分类正确的样本数占样本总数的比例
a
c
c
(
f
;
D
)
=
∫
(
f
(
x
)
=
y
)
p
(
x
)
d
x
=
1
?
E
(
f
;
D
)
acc\left( f;D \right) =\int{\left( f\left( x \right) =y \right) p\left( x \right) dx}\\=1-E\left( f;D \right)
acc(f;D)=∫(f(x)=y)p(x)dx=1?E(f;D)
3.2查准率、查全率与 F 1 F1 F1
| 真实 | 预测结果 | 预测结果 |
|---|---|---|
| 情况 | 正例 | 反例 |
| 正例 | TP(真正例) | FN(假正例) |
| 反例 | FP(假正例) | TN(真反例) |
查准率P
P
=
T
P
T
P
+
F
P
P=\frac{TP}{TP+FP}
P=TP+FPTP?
查全率R
R
=
T
P
T
P
+
F
N
R=\frac{TP}{TP+FN}
R=TP+FNTP?
查准率和查全率是一对矛盾的度量
为了能够更好的观察出哪一个学习器最优,以前构建了以下图所示的P-R曲线图
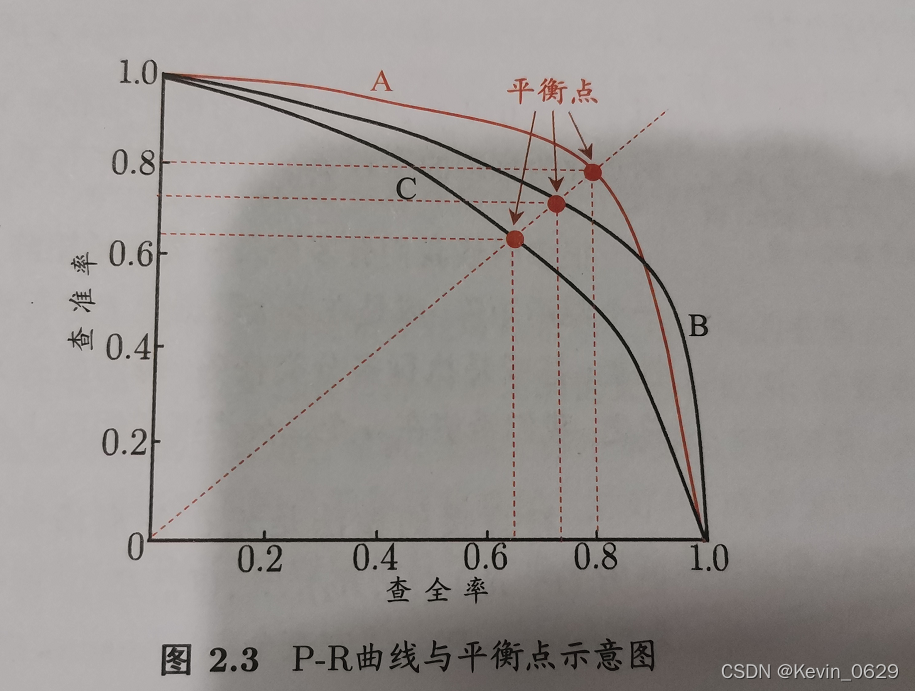
一个好的学习器的评判标准如下
- 如果一个学习器的曲线包裹这另外一个学习器的曲线,那么这个包裹的学习器的曲线优于被包裹的
- 比较两个P-R曲线所包围的面积
- 使用“平衡点”,即采用
y
=
x
y=x
y=x穿过一三象限的直线,找出曲线与这条直线所交叉的位置,查准率=查全率,此时的值称为BEP,而通过比较BEP的值便可以知道哪一个学习器更优
使用BEP难免过于简化,因此引入F1的概念
常用的F1度量是
F 1 = 2 × P × R P + R = 2 × T P 样例总数 + T P ? T N F1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{\text{样例总数}+TP-TN} F1=P+R2×P×R?=样例总数+TP?TN2×TP?
F1度量的一般形式 F β F_{\beta} Fβ?
F β = ( 1 + β 2 ) × P × R ( β 2 × P ) + R F_{\beta}=\frac{\left( 1+\beta ^2 \right) \times P\times R}{\left( \beta ^2\times P \right) +R} Fβ?=(β2×P)+R(1+β2)×P×R?
其中有以下 β \beta β的取值, β \beta β>0度量了查全率对查准率的相对重要性, β \beta β=1度量了标准的F1, β \beta β>1时查全率有更大影响, β \beta β<1查准率有更大影响
书上还列出了许许多多的其他关于查准率和查全率的变形,这里就不一一列举出来了
3.3 ROC与AUC
ROC是研究学习器泛化性能的有力工具,根据学习器的预测结果对样例进行排序,按此顺序逐个把样本作为正例进行预测,每次计算出两个重要量的值,分别以它们作为横、纵坐标作图,ROC曲线的纵轴是“真正例率(TPR)”,横轴是“假正例率(FPR)”,其中TPR的定义如下
T
P
R
=
T
P
T
P
+
F
N
TPR=\frac{TP}{TP+FN}
TPR=TP+FNTP?
FPR定义如下
F
P
R
=
F
P
T
N
+
F
P
FPR=\frac{FP}{TN+FP}
FPR=TN+FPFP?
那么如何通过ROC曲线图来判断学习器与学习器的优劣呢?
答:通过ROC与X、Y轴围成的面积AUC来表示出学习器的好坏,其中AUC的定义如下
A
U
C
=
1
2
∑
i
=
1
m
?
1
(
x
i
+
1
?
x
i
)
(
y
i
+
y
i
+
1
)
AUC=\frac{1}{2}\sum_{i=1}^{m-1}{\left( x_{i+1}-x_i \right)}\left( y_i+y_{i+1} \right)
AUC=21?i=1∑m?1?(xi+1??xi?)(yi?+yi+1?)
3.4 代价敏感错误率与代价曲线
当学习器发生错误的时候,前面的学习器默认发生错误时候所产生的代价是一样的,但是现实中的代价并不是统一的,因此便有了下面的代价敏感错误率
E
(
f
;
D
;
cos
?
t
)
=
1
m
(
∑
x
i
∈
D
+
I
I
(
f
(
x
i
)
≠
y
i
)
×
cos
?
t
01
+
∑
x
i
∈
D
?
I
I
(
f
(
x
i
)
≠
y
i
)
×
cos
?
t
10
)
E\left( f;D;\cos t \right) =\frac{1}{m}\left( \sum_{x_i\in D^+}^{}{II\left( f\left( x_i \right) \ne y_i \right) \times \cos t_{01}+\sum_{x_i\in D^-}^{}{II\left( f\left( x_i \right) \ne y_i \right) \times \cos t_{10}}} \right)
E(f;D;cost)=m1?(xi?∈D+∑?II(f(xi?)?=yi?)×cost01?+xi?∈D?∑?II(f(xi?)?=yi?)×cost10?)
绘制代价曲线图,首先FNR假反例率定义如下
F
N
R
=
1
?
T
P
R
FNR=1-TPR
FNR=1?TPR
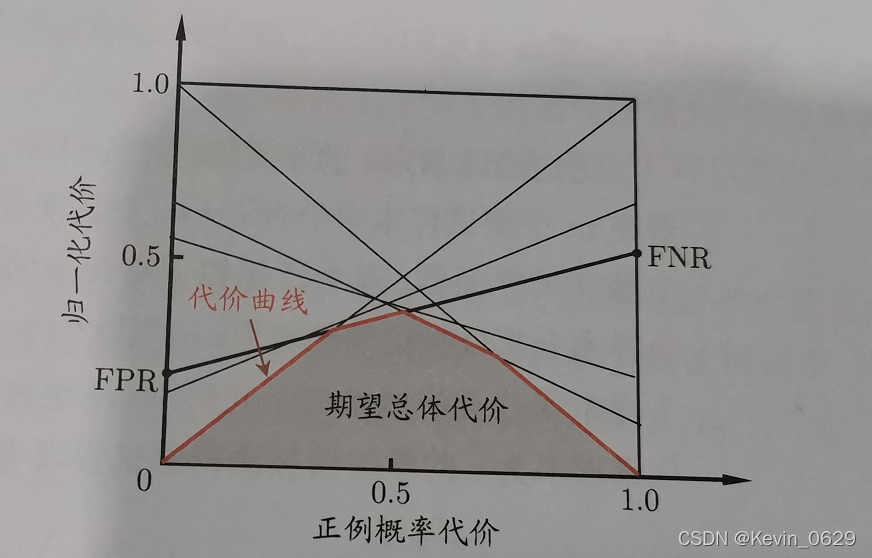
在ROC曲线上每一点对应了代价平面上的一条线段,设ROC曲线上的点坐标为(FPR,TPR),则可以计算相应的FNR,然后在代价平面上绘制一条从(0,FPR)到(1,FNR)的线段,线段下的面积即表示了该条件下的期望的总体代价,书本给出的代价函数例子如下图所示,
四、比较检验
我通过阅读书上的内容以及结合了github上一个博主所写的内容进行理解假设检验&方差&偏差
五、总结
通过阅读本章,我对学习器的评判的好坏的标准以及如何量化其好坏结果有了一定的了解,但是对检验这一块仍然存在着一定的知识盲区,希望这些盲区可以在以后读西瓜书的过程中能够彻底消化理解