[人工智能]【统计学习方法】学习笔记——第一章：统计学习及监督学习概论（实践）

1. 最小二乘法

1.1 最小二乘法的原理与要解决的问题

高斯于1823年在误差e1 ,… , en独立同分布的假定下，证明了最小二乘方法的一个最优性质: 在所有无偏的线性估计类中，最小二乘方法是其中方差最小的！
最小二乘法是由勒让德在19世纪发现的，形式如下式：
$$目标函数=\sum (观测值?理论值{)}^2$$
观测值就是我们的多组样本，理论值就是我们的假设拟合函数。目标函数也就是在机器学习中常说的损失函数，我们的目标是得到使目标函数最小化时候的拟合函数的模型。
举一个最简单的线性回归的简单例子，比如我们有$m$个只有一个特征的样本：$(x_i,y_i)(i=1,2,3...,m)$

样本采用一般的 $h_{\theta }(x)$ 为$n$次的多项式拟合，$h_{\theta }(x)={\theta }_0+{\theta }_1(x)+{\theta }_2{x}^2+...+{\theta }_n{x}^n$，$\theta ({\theta }_0,{\theta }_1,{\theta }_2,...,{\theta }_n)$为参数。

最小二乘法就是要找到一组$\theta ({\theta }_0,{\theta }_1,{\theta }_2,...,{\theta }_n)$使得 ${\sum }_{i=1}^n(h_{\theta }(x_i)?y_i{)}^2$(残差平方和) 最小，即，求$\min {\sum }_{i=1}^n(h_{\theta }(x_i)?y_i{)}^2$

1.2 最小二乘法的矩阵法解法

最小二乘法的代数法解法就是对${\theta }_i$求偏导数，令偏导数为0，再解方程，得到${\theta }_i$。矩阵法比代数法要简介。下面介绍矩阵法解法，这里用多元线性回归例子来描述：
假设函数$h_{\theta }(x_1,x_2,...,x_n)={\theta }_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n$的矩阵表达方式为：
$$h_{\theta }(X)=X\theta$$
其中，假设函数$h_{\theta }(X)=X\theta$为$m\times 1$的向量，$\theta$为$n\times 1$的向量。里面有n个代数法的模型参数。$X$为$m\times n$维的矩阵，$m$代表样本的个数，$n$代表样本的特征数。

损失函数定义为$J(\theta )=\frac{1}{2}(X\theta ?Y{)}^T(X\theta ?Y)$，其中$Y$是样本的输出向量，维度维$m\times 1$。KaTeX parse error: Undefined control sequence: \2 at position 2: 1\?2?在这里是为了求导后的系数为1，方便计算。

根据最小二乘法的原理，要对这个损失函数对$\theta$向量求导0，结果如下式：
$$\frac{?}{?\theta }J(\theta )=X^T(X\theta ?Y)=0$$
对上述求导等式整理后可得：
$$\theta =(X^{T}X{)}^{?1}{X}^{T}Y$$

1.3 最小二乘法的几何解释

结论：最小二乘法的几何意义是高维空间中的一个向量在低维子空间的投影。

1.4 最小二乘法的局限性和适用场景

最小二乘法适用简洁高效，比梯度下降这样的迭代法方便很多，但是有一些局限性：

• 首先，最小二乘法需要计算$X^{T}X$的逆矩阵，有可能它的逆矩阵不存在。这样就不能直接适用最小二乘法。此时梯度下降仍然可用。当然，可以通过对样本数据进行整理，去掉冗余特征。让$X^{T}X$的行列式不为0，然后继续适用最小二乘法。
• 第二，当样本特征$n$非常大的时候，计算$X^{T}X$的逆矩阵是一个非常耗时的工作（$n\times n$的矩阵求逆），甚至不可行。此时以梯度下降为代表的迭代法仍然可以适用。那这个$n$到底多大就不适合最小二乘法呢？如果没有很多的分布式大数据计算资源，建议超过10000个特征就用迭代法。或者通过主成分分析降低特征的维度后再用最小二乘法。
• 第三，如果拟合函数不是线性的，这时无法适用最小二乘法，需要通过一些技巧转化为线性才能适用。此时梯度下降仍然可用。

2. 最小二乘法Python实现

假设我们的目标函数$y=\sin 2\pi x$，加上一个正态分布的噪音干扰，用多项式去拟合。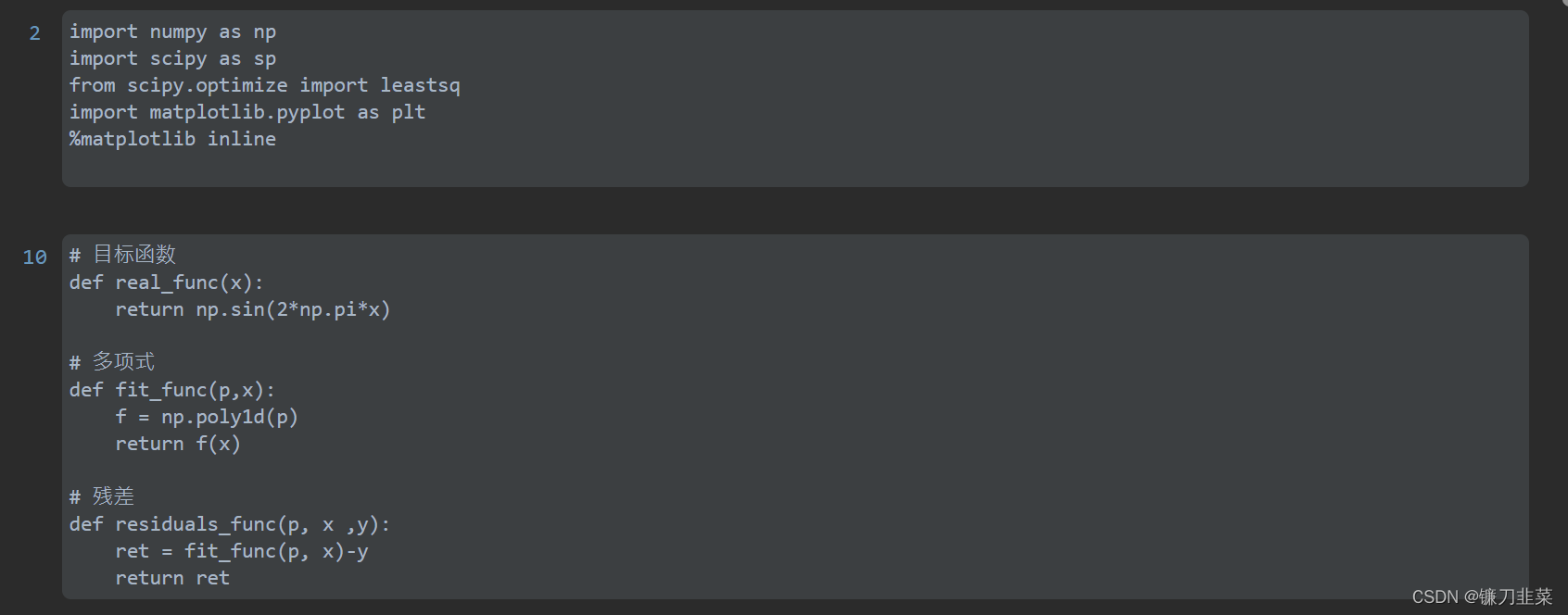





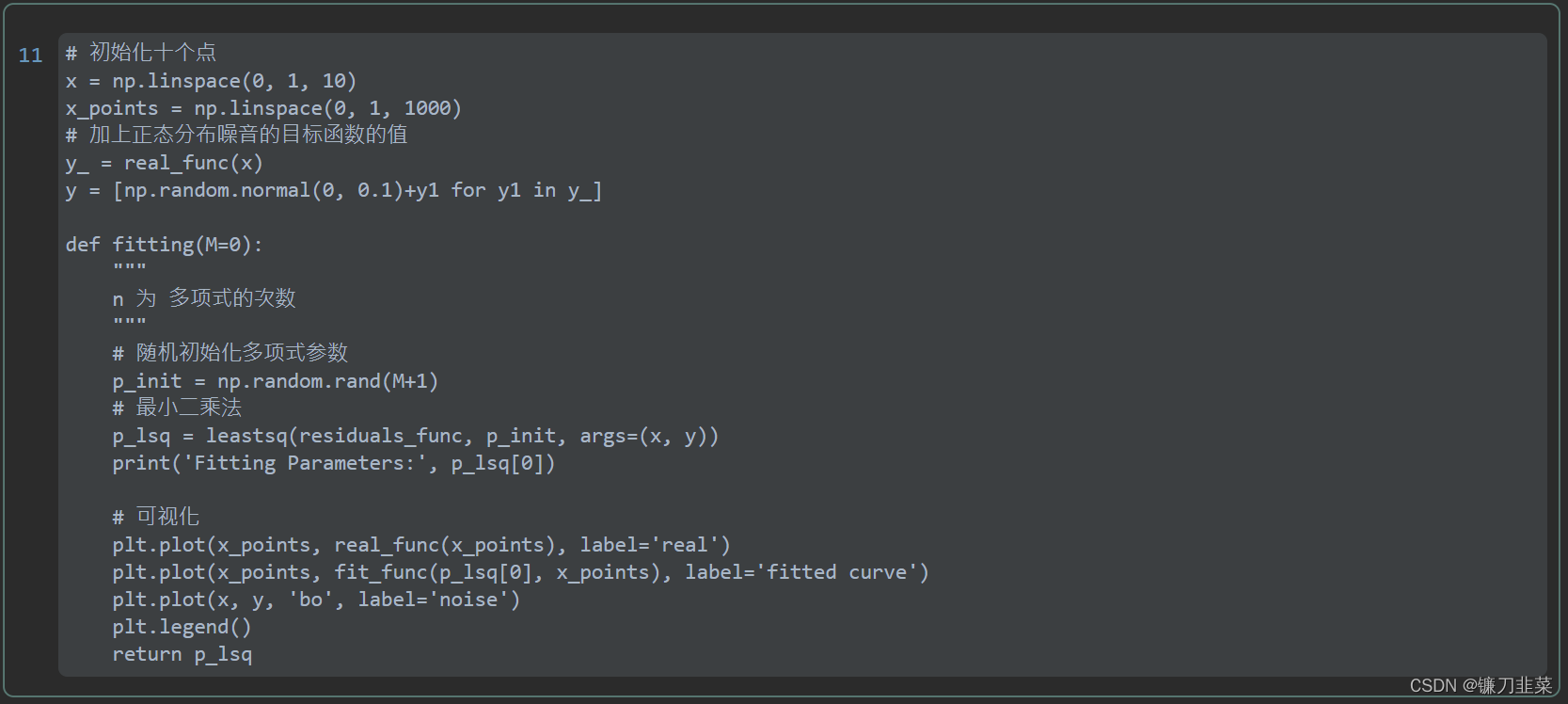
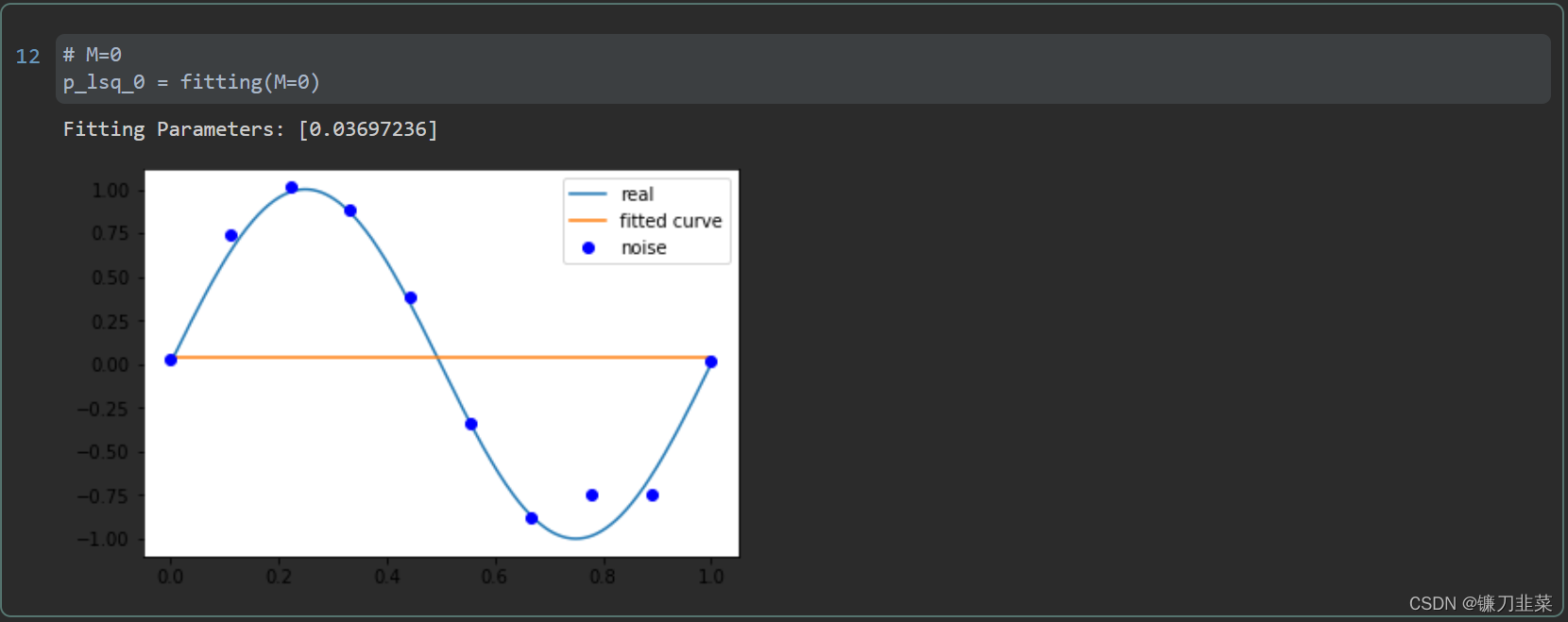
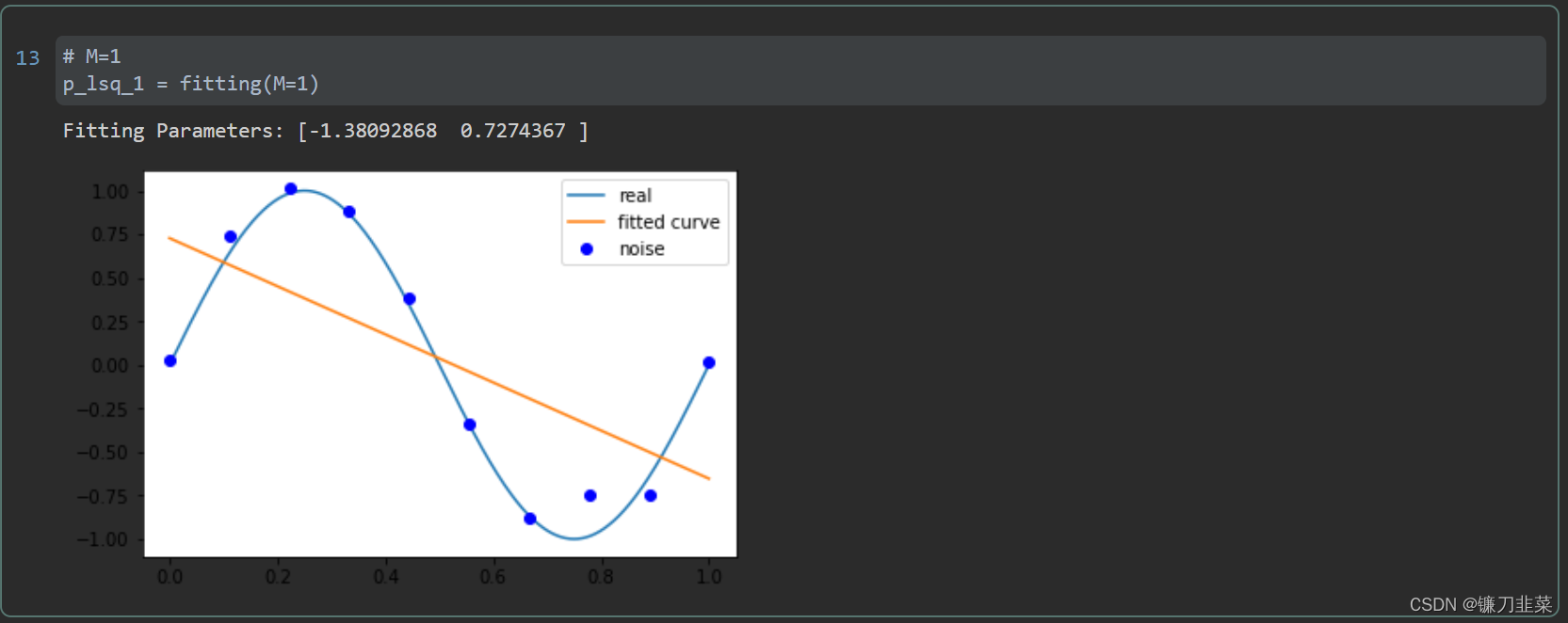
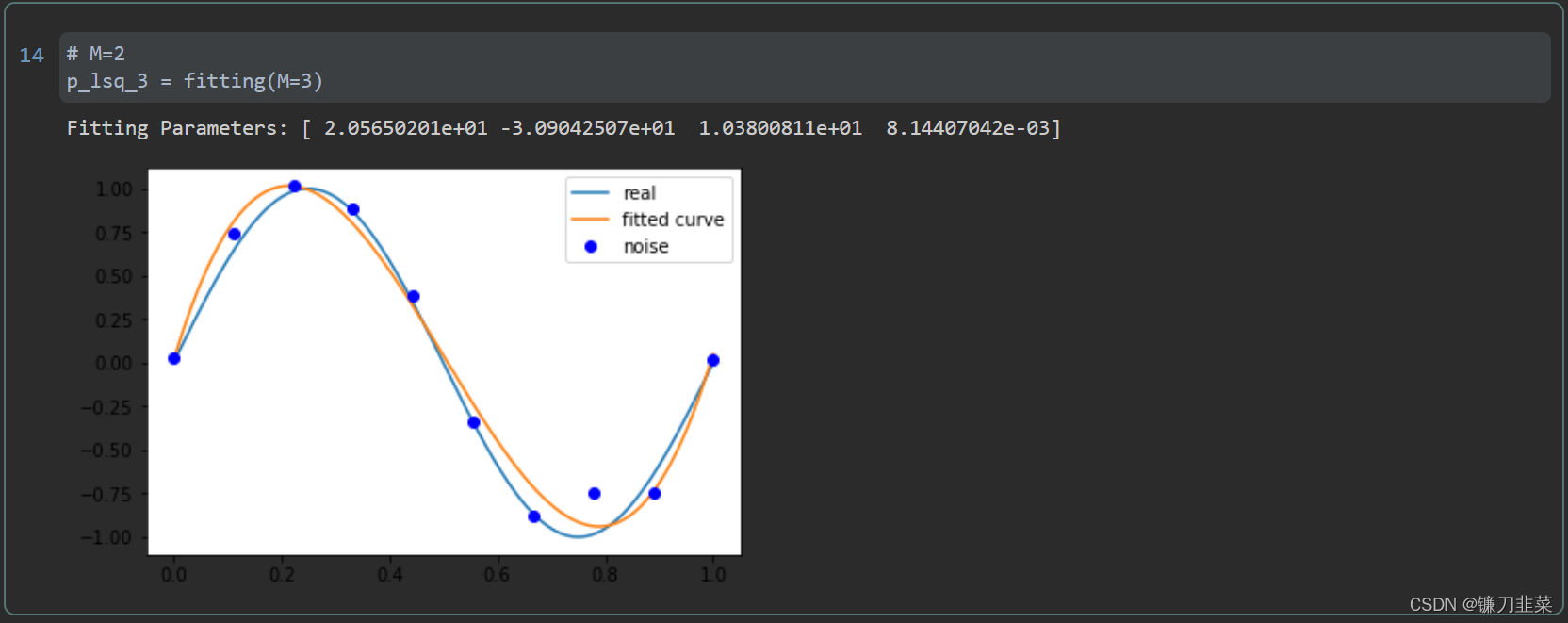
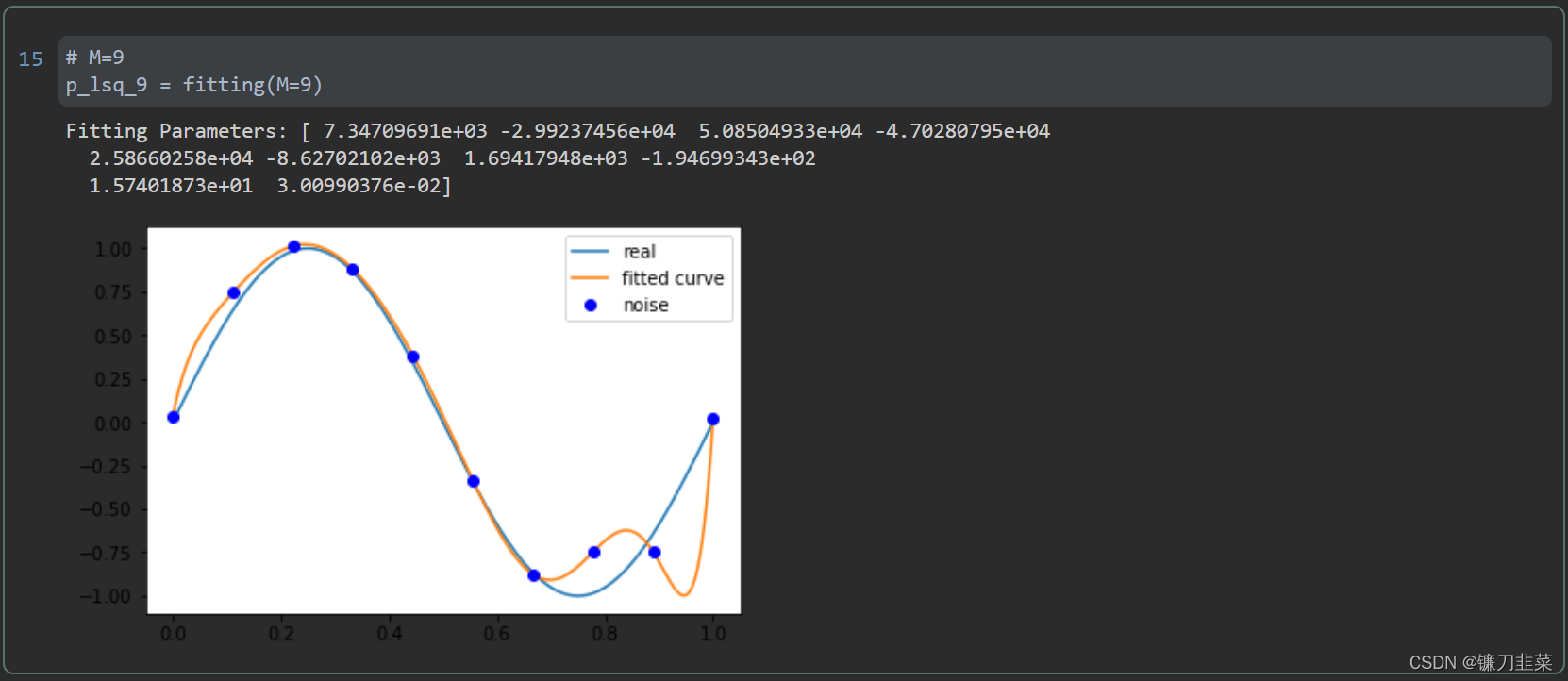
由上图可见，当M=9时，多项式曲线通过了每个数据点，但是造成了过拟合。

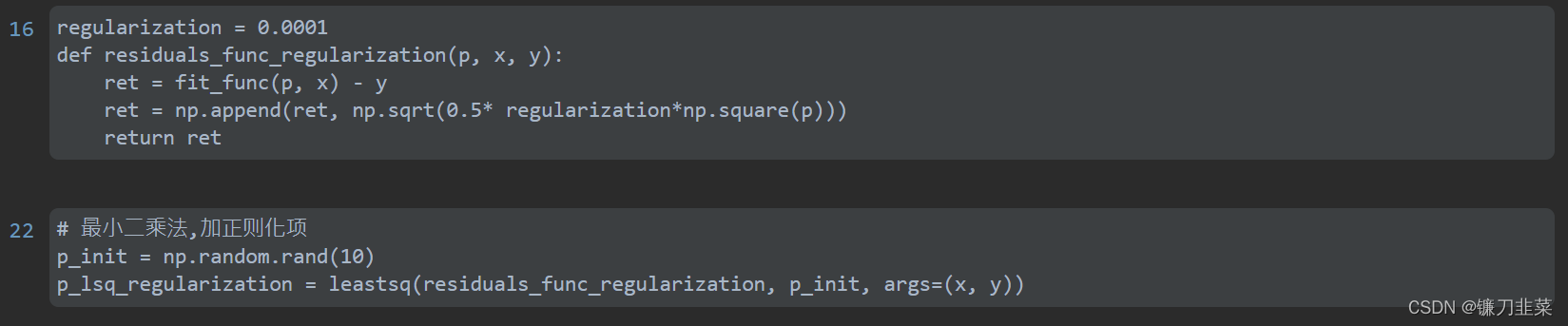
正则化

通过引入正则化项（regularizer）来降低过拟合。
$$Q(x)=\sum _{i=1}^n(h(x_i)?y_i{)}^2+\lambda ||\omega |{|}^2$$
在回归问题中，损失函数是平方损失，正则化可以是参数向量的$L2$范数，也可以是$L1$范数。

L1: regularization*abs(p)
L2:0.5* regularization * np.square(p)

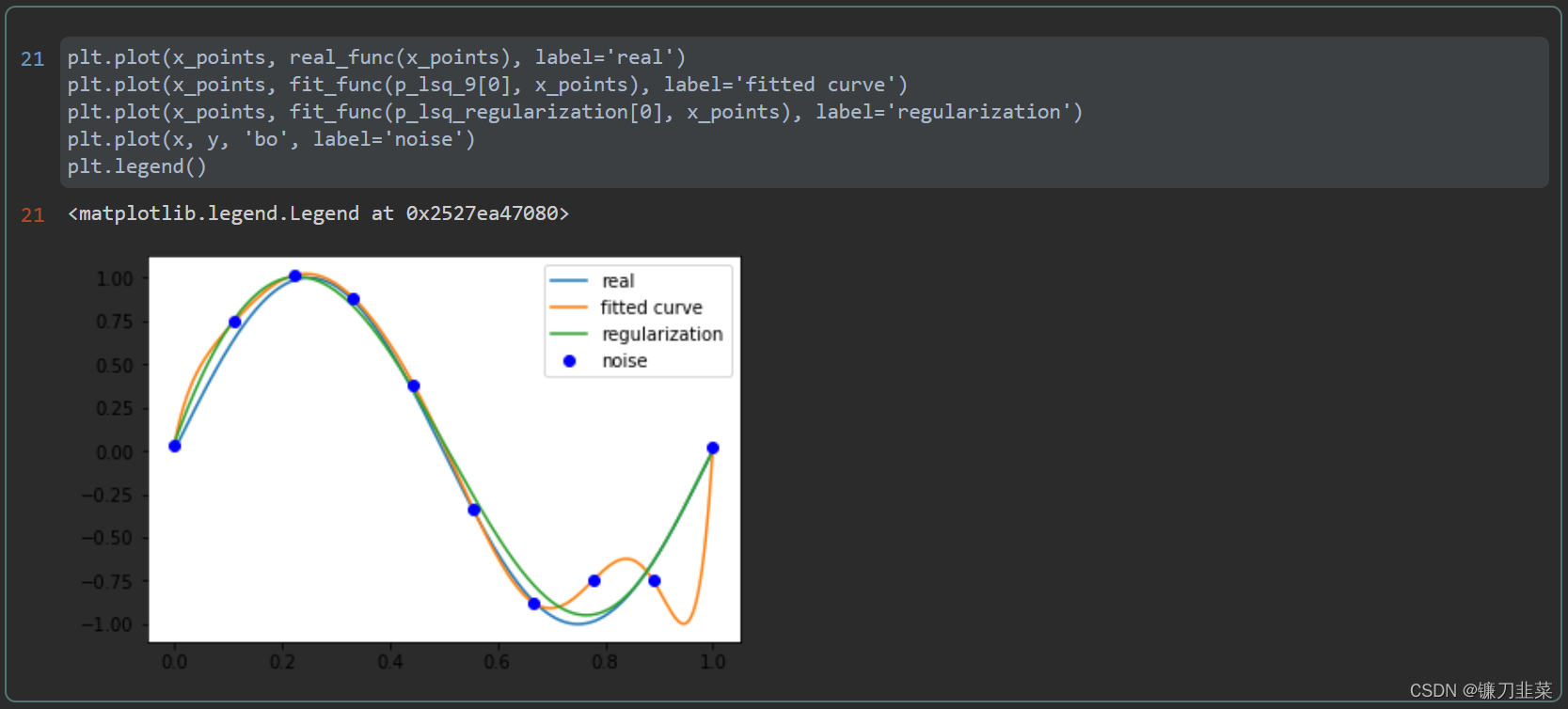
参考资料

1. https://zhuanlan.zhihu.com/p/38128785
2. 《统计学习方法》 李航 著
3. https://github.com/wzyonggege/statistical-learning-method/