1.MINST数据集下载

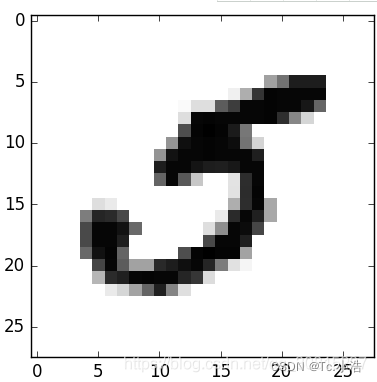
数据共有7万张图片，每张图片有784个特征。因为图片是28×28像素，每个特征代表了一个像素点的强度，从0（白色）到255（黑色），X[36000]的数字如下，通过“y[36000]”查看其标签为“5”。
在这里插入图片描述

import os
import os.path
import urllib
import gzip
import shutil
import numpy as np
import matplotlib.pyplot as plt
#目录的创建
if not os.path.exists('mnist'):
    os.mkdir("mnist")

#下载数据集
def download_and_gzip(name):
    if not os.path.exists(name+'.gz'):   
        urllib.request.urlretrieve('http://yann.lecun.com/exdb/'+name+'.gz', name+'.gz')
    if not os.path.exists(name):
        with gzip.open(name+'.gz', "rb") as f_in, open(name, 'wb') as f_out:
            shutil.copyfileobj(f_in,f_out)

#数据集的类型
download_and_gzip("mnist/train-images-idx3-ubyte")
download_and_gzip('mnist/train-labels-idx1-ubyte')
download_and_gzip('mnist/t10k-images-idx3-ubyte')
download_and_gzip("mnist/t10k-labels-idx1-ubyte")

#训练和测试数据集的划分
def load_mnist():
    loaded = np.fromfile("mnist/train-images-idx3-ubyte", dtype='uint8')
    train_x = loaded[16:].reshape(60000,28,28)
    loaded = np.fromfile("mnist/t10k-images-idx3-ubyte", dtype='uint8')
    test_x = loaded[16:].reshape(10000,28,28)
    loaded = np.fromfile('mnist/train-labels-idx1-ubyte', dtype='uint8')
    train_y = loaded[8:].reshape(60000)
    loaded = np.fromfile("mnist/t10k-labels-idx1-ubyte", dtype='uint8')
    test_y = loaded[8:].reshape(10000)
    return train_x, train_y, test_x, test_y

#绘图方法
def plot_images(images, row, col):
    show_image = np.vstack(np.split(np.hstack(images[:col*row]),row, axis=1))
    plt.imshow(show_image,cmap='binary')
    plt.axis("off")
    plt.show()


row, col = 4, 5
# train_x, train_y, test_x, test_y = load_mnist()
# plot_images(train_x, row, col)

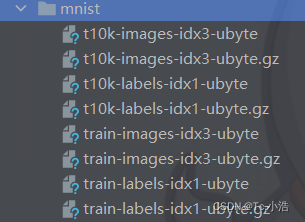
数据集下载完成的目录和文件
在这里插入图片描述

2.训练一个二元分类器

2.1随机梯度下降（SGD）分类器

现在先简化问题，只尝试识别一个数字——比如数字5。那么这个“数字5检测器”就是一个二元分类器的例子，它只能区分两个类别：5和非5。先为此分类任务创建目标向量(将数字标签转换为bool型标签true代表 5，false代表非5)：

y_train_5 = (y_train == 5) # True for all 5s, False for all other digits.
y_test_5 = (y_test == 5)

接着挑选一个分类器并开始训练。一个好的初始选择是随机梯度下降（SGD）分类器，使用Scikit-Learn的SGDClassifier类即可。这个分类器的优势是，能够有效处理非常大型的数据集。这部分是因为SGD独立处理训练实例，一次一个。此时先创建一个SGDClassifier并在整个训练集上进行训练：

from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
sgd_clf.predict([digit_5])

梯度下降法（SGD）是一个简单有效的方法，用于判断使用凸loss函数（convex loss function）的分类器（SVM或logistic回归）。SGD被成功地应用在大规模稀疏机器学习问题上（large-scale and sparse machine learning），经常用在文本分类及自然语言处理上。假如数据是稀疏的，该模块的分类器可以轻松地解决这样的问题：超过 $10^5$
的训练样本、超过 $10^5$ 的features。
SGD的优点：

高效
容易实现
SGD的缺点是：
SGD需要许多超参数：比如正则项参数、迭代数
SGD对于特征归一化是敏感的
注意：SGD是一种优化方法，不是分类算法，SGDClassifier函数实际使用的是SVM或logistic回归算法进行分类！！！

当说到召回率的时候就说到了混淆矩阵。

再回顾一下召回率吧，案例中有100个正例，猜中(预测对)了59个，我们就说召回率为59%。

召回率就是猜中率。

当时也讲到，正例和反例，加上猜中和猜错，总共有四种情况

举个好理解的例子：
已知条件：班级有100人，男生80人，女生20人。
目标：找出所有女生。
结果：从中选中50人，女生20人，男生30人。

	相关(Relevant)，正类	无关(NonRelevant),负类
被检测到(Retrieved)	true positives(TP）正类判定为正类，例子中就是正确的判断“是女生”)	false positives(FP)负类判定为正类，例子中就是分明是男生，缺判断为女生
未被检测到(Not Retrieved)	false negatives(FN）正类判定为负类)，例子中，分明是女生，缺判断为男生	true negatives(TN)负类判定为负类，就是一个男生被判断为男生)

TP=20,FP=30,FN=0,TN=50
做一个单独的正类预测，并确保它是正确的，就可以得到完美精度（精度＝1/1＝100%）。但这没什么意义，因为分类器会忽略这个正类实例之外的所有内容。因此，精度通常与另一个指标一起使用，这个指标就是召回率（recall），也称为灵敏度（sensitivity）或者真正类率（TPR）：它是分类器正确检测到的正类实例的比率.

精度：precision=TP/TP+FP=20/50=0.4
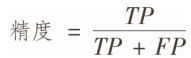
在这里插入图片描述

召回率：recall=TP/TP+FN=20/20=1
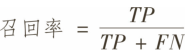
在这里插入图片描述

因此我们可以很方便地将精度和召回率组合成一个单一的指标，称为F1 分数。当你需要一个简单的方法来比较两种分类器时。F1 分数是精度和召回率的谐波平均值。谐波平均值会给予较低的值更高的权重。因此，只有当召回率和精度都很高时，分类器才能得到较高的F1 分数。
在这里插入图片描述
参考：https://blog.csdn.net/qq_30815237/article/details/87972110