之前做的L2项目,都是高速、高架场景,地图传输格式ADASISv3就够了。现在要推广到城市场景,原来的框架或协议可能不够用了,所以打算学习下Lanelet2这套新的高精度地图框架。
参考资料:
- Lanelet2: A high-definition map framework for the future of automated driving
- Pathfinding and Routing for Automated Driving in the Lanelet2 Map Framework
- Lanelet Primitives
- Lanelet Maps
现有地图格式框架的问题
在自动驾驶领域,高精地图常被应用于以下几个方面:
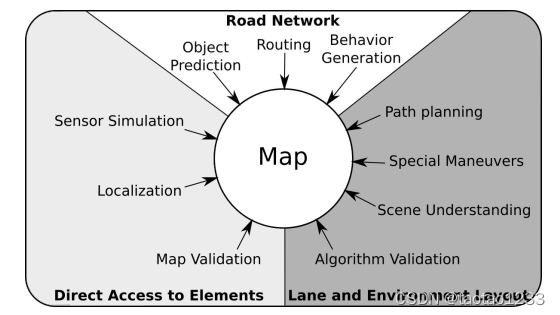
?比如:
- 对于定位问题和地图验证,需要依赖路面元素的位置,比如地面标记,交通牌,马路沿线。
- 对于行为决策,需要依赖于特定车道下的交通信号灯。
- 对于交通参与者运动的预测,必须先知道适用于它们的交通规则,明天这些目标接下来可能往哪这里运动,而不是单单借助于传感器感知,不然对于行人运动预测来说是不可能的。
- 对于路径导航,需要清晰的知道道路链接拓扑关系以及交通法规限制。
以往的地图框架,比如openstreetmap(OSM),采用自上而下的设计思路。道路road被一条虚拟车道中心线center line表达。它已被广泛使用于导航设备。其他车道信息,比如交通线和道路边界的位置,都以属性的形式附加到这条中心线上。
随着ADAS需求的增加,越来越多的属性将被增加。这使得地图信息极度复杂且无法直接被表示。比如,路边目标的绝对位置,只能通过中心线左右边界的偏移量以及道路宽度间接推算出来。如果是十字路口,没有中心线的,那将变得更加困难。 作者认为opendrive也有同样的问题。
Lanelet2 组件及概念
Lanelet2主要包含如下图层:
- physical layer 包含真实的,所有可以被观测到的地图元素,比如路面标记、交通灯、路边石头等等。
- relational layer 包含所有对pyhical layer元素的抽象表述,比如对于车道的交通规则,这样所有的地图信息都有道路实体元素承载。
- topological layer 邻居关系和上下文关系,通过relational layer隐式获取。
上述层级结构主要由Points, linestrings, polygons, lanelets, areas and regulatory elements 共六个元素表达,每个元素的实体都拥有独立的ID号,数据属性通过键值对储存。
Points
包含ID, 3D坐标和属性。关于高程,天朝图商不让发布高程信息,所以可以采用2.5D的形式,主要用于区分隧道和桥梁,一般的路面高程为0,碰到隧道或桥梁,可以设置为1,表示这里有新的图层,这对于路径规划很重要。
另外,单个点是没有意义的,在lanelet2中必须同其他对象一起使用才有意义。
point可以由osm格式中的node表示。
Linestrings
也被认为是多项式曲线,由一系列的point通过线性插值表达,如下图所示。linestring由三个绿色的point经过插值后表达。包含ID,类型,以及point数组。?
lanelstring可以由OSM格式中的way来表示。

Polygons
多边形同linestring类似,只是它构成了一个区域,言下之意是它的point数组中,第一个point和最后一个point是相互链接的。它通常被用于描述自定义区域或交通牌。
它同样可以由OSM中的way表示。
Lanelets
lanelet 是对车道的原子描述。原子意味着交通规则在这条lanelet上不会改变。
lanelet可以有OSM格式中的relation表示,包含多种way以及交通元素
lanelet由左右边界构成,边界由linestring表达,同一条车道的两条linestring方向必须相同。另外lanelet还包含车道中心线,且默认是单向的。相邻的lanelet需要共享linestring。
每个lanelet可以绑定交通元素,比如限速、限行
如下图所示,9个点,三条linestrings构成了两条Lanelets,包含2个ID,以及车辆可以通信的标记
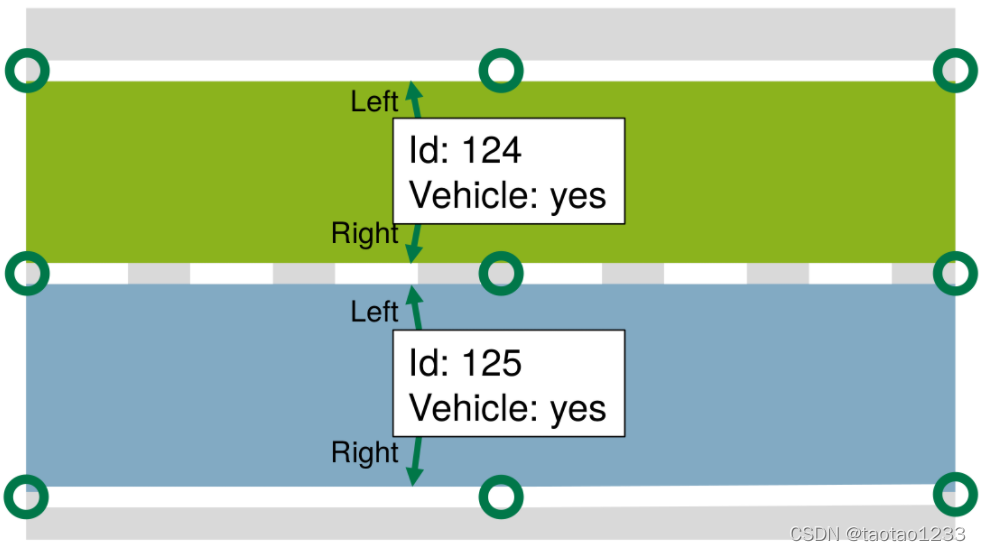
Areas?
area同lanelet的区别是,area可以用于表达无向的交通环境(比如停车场),而lanelet只能表达有向的交通环境。同一个area内的交通规则不可更改。
Area内部运行有空洞,表示改区域不可访问。但是空洞内部不允许有别的area或linestring
area由一组linestring按照顺时针顺序描述,如下图所示,ID 126和 ID 127是两片用于停车的区域。?

Regulatory element
交通元素被lanelet或area索引,用tag表示具体的交通规则。如下图所示,交通元素ID 126为红绿灯。
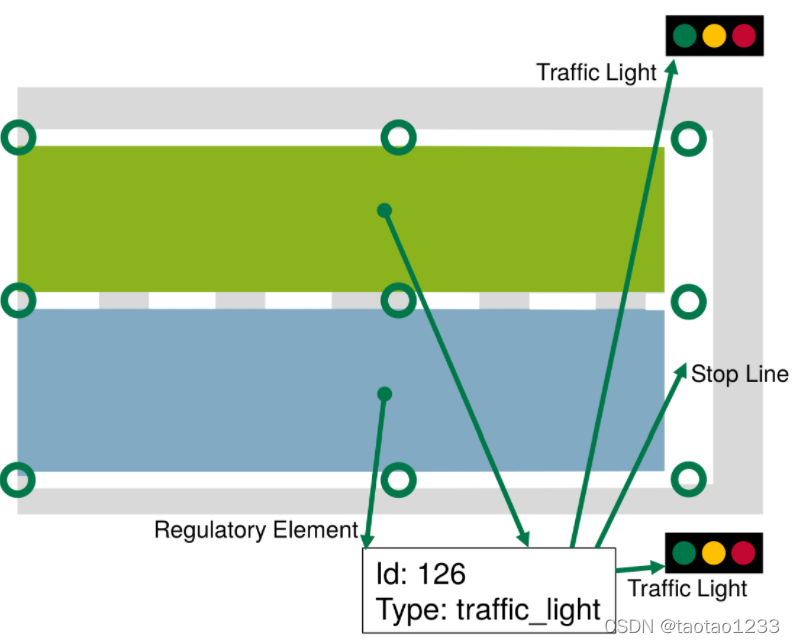
下面是一则综合案例,表达了6个元素与3个图层之间的关系。

Lanelet 距离公式理解
如何计算lanelet外一点X距离该lanelet的距离?
给定外点X,其坐标(x,y)已知,假设linestring的端点b和t的位置和梯度方向也是知道的。
我们知道lanelet是有多个points的线性插值得到polyline表述,我们无法知道X到这条polyline的解析解(缺乏polyline的曲线系数)

?为此,我们对梯度方向和位置同时插值有下式:
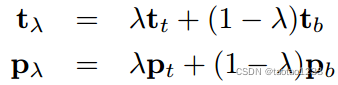
另外,根据向量关系有:
![]()
同时,我们知道垂直约束关系:
![]()
?假设在原点(0,0),
坐标为(l,0),它们对应的梯度方向为(1,
)和(1,
),那么联立上面所有公式,整理得到变量
为:
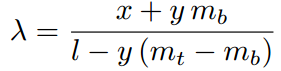
?有了这个插值比例后,我们就知道了,从而可以知道模长,也就是距离。