目录
1 导入数据查看相关信息

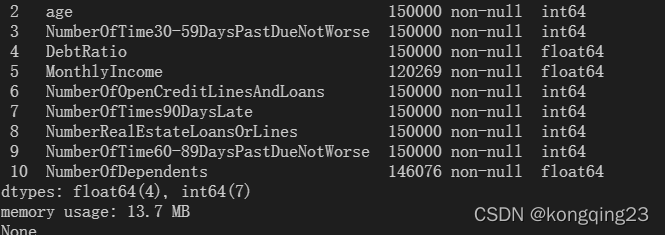
 2 数据预处理
2 数据预处理
2.1 去重复值+更新索引
删除重复数据以后,索引依然是原来的数值,一定要记得更新为删除完重复数据之后的样本数量。

2.2 填补缺失值
查看缺失值比例
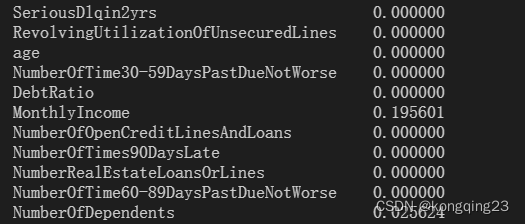
针对于该数据,我们需要填充的是月收入和家属人数。
家属人数缺失很少,仅缺失了大约2.5%
,可以考虑直接删除,或者使用均值来填补。
“
收入
”
缺失了几乎
20%
,并且我们知道,
“
收入
”
必然是一个对信用评分来说很重要的因素,因此这个特征必须要进行填补。
对于月收入的缺失,一个来借钱的人应该是会知道,
“
高收入”
或者
“
稳定收入
”
于他
/
她自己而言会是申请贷款过程中的一个助力,因此如果收入稳定良好的人,肯定会倾向于写上自己的收入情况,那么这些“
收入
”
栏缺失的人,更可能是收入状况不稳定或收入比较低的人。基于这种判断,我们可以用比如说,四分位数来填补缺失值,把所有收入为空的客户都当成是低收入人群。当然了,也有可能这些缺失是银行数据收集过程中的失误,我们并无法判断为什么收入栏会有缺失,所以我们的推断也有可能是不正确的。具体采用什么样的手段填补缺失值,要和业务人员去沟通,观察缺失值是如何产生的。在这里,我们使用随机森林填补
收入。
对于一个有
n
个特征的数据来说,其中特征
T
有缺失值,我们就把特征
T
当作标签,其他的n-1
个特征和原本的标签组成新的特征矩阵。那对于
T
来说,它没有缺失的部分,就是我们的Y_train,这部分数据既有标签也有特征,而它缺失的部分,只有特征没有标签,就是我们需要预测的部分。
特征
T
不缺失的值对应的其他
n-1
个特征
+
本来的标签:
X_train
特征
T
不缺失的值:
Y_train
特征
T
缺失的值对应的其他n-1
个特征
+
本来的标签:
X_test
特征
T
缺失的值:未知,我们需要预测的
Y_test。
注意,使用随机森林填充缺失值时,要保证只有一个特征值缺失,一定要注意此时数据的获取位置。
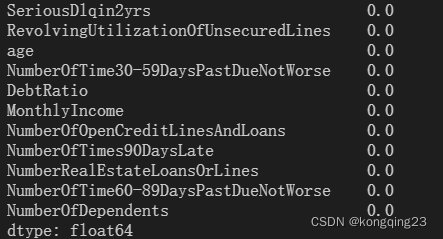
?
2.3 处理易操作
现实数据永远都会有一些异常值,首先我们要去把他们捕捉出来,然后观察他们的性质。注意,我们并不是要排除掉所有异常值,相反很多时候,异常值是我们的重点研究对象,比如说,双十一中购买量超高的品牌,或课堂上让很多学生都兴奋的课题,这些是我们要重点研究观察的。
日常处理异常值,我们使用箱线图或者 法则来找到异常值。但在银行数据中,我们希望排除的“
异常值
”
不是一些超高或超低的数字,而是一些不符合常理的数据:比如,收入不能为负数,但是一个超高水平的收入却是合理的,可以存在的。所以在银行业中,我们往往就使用普通的描述性统计来观察数据的异常与否与数据的分布情况。注意,这种方法只能在特征量有限的情况下进行,如果有几百个特征又无法成功降维或特征选择不管用,那还是用比较好。
虽然大家都在努力防范信用风险,但实际违约的人并不多。并且,银行并不会真的一棒子打死所有会违约的人,很多人是会还钱的,只是忘记了还款日,很多人是不愿意欠人钱的,但是当时真的很困难,资金周转不过来,所以发生逾期,但一旦他有了钱,他就会把钱换上。对于银行来说,只要你最后能够把钱还上,我都愿意借钱给你,因为我借给你就有收入(利息)。所以,对于银行来说,真正想要被判别出来的其实是”
恶意违约
“
的人,而这部分人数非常非常少,样本就会不均衡。这一直是银行业建模的一个痛点:我们永远希望捕捉少数类。
之前提到过,逻辑回归中使用最多的是上采样方法来平衡样本。
2.4 划分训练集和测试集并保存
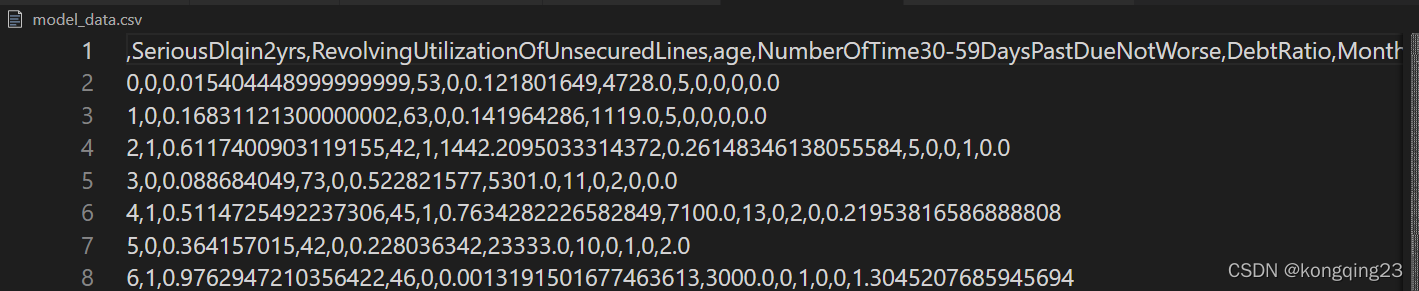
 ?
?
?
3 分箱
我们要制作评分卡,是要给各个特征进行分档,以便业务人员能够根据新客户填写的信息为客户打
分。因此在评分卡制作过程中,一个重要的步骤就是分箱。可以说,分箱是评分卡最难,也是最核心的思路,分箱的本质,其实就是离散化连续变量,好让拥有不同属性的人被分成不同的类别(打上不同的分数),其实本质比较类似于聚类。
离散化连续变量必然伴随着信息的损失,并且箱子越少,信息损失越大。为了衡量特征上的信息量以及特征对预测函数的贡献,银行业定义了概念Information value(IV)
:
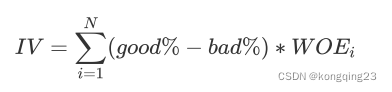
其中
N
是这个特征上箱子的个数,
i
代表每个箱子,good%是这个箱内的优质客户(标签为0
的客户)占整个特征中所有优质客户的比例,bad%是这个箱子里的坏客户(就是那些会违约,标签为1
的那些客户)占整个特征中所有坏客户的比例。
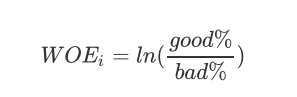
这是我们在银行业中用来衡量违约概率的指标,中文叫做证据权重
(weight of Evidence)
,本质其实就是优质客户比上坏客户的比例的对数。WOE
是对一个箱子来说的,
WOE
越大,代表了这个箱子里的优质客户越多。而
IV
是对整个特征来说的,IV
代表的意义是我们特征上的信息量以及这个特征对模型的贡献。

?
IV
并非越大越好,我们想要找到
IV
的大小和箱子个数的平衡点。箱子越多,IV必然越小,因为信息损失会非常多,所以,我们会对特征进行分箱,然后计算每个特征在每个箱子数目下的WOE
值,利用
IV
值的曲线,找出合适的分箱个数。
我们希望不同属性的人有不同的分数,因此我们希望在同一个箱子内的人的属性是尽量相似的,而不同箱子的人的属性是尽量不同的,即业界常说的”
组间差异大,组内差异小
“
。对于评分卡来说,就是说我们希望一个箱子内的人违约概率是类似的,而不同箱子的人的违约概率差距很大,即WOE
差距要大,并且每个箱子中坏客户所占的比重也要不同。那我们,可以使用卡方检验来对比两个箱子之间的相似性,如果两个箱子之间卡方检验的P
值很大,则说明他们非常相似,那我们就可以将这两个箱子合并为一个箱子。
?
利用卡方检验画箱子数量的学习曲线,找出最适合的分箱个数。
?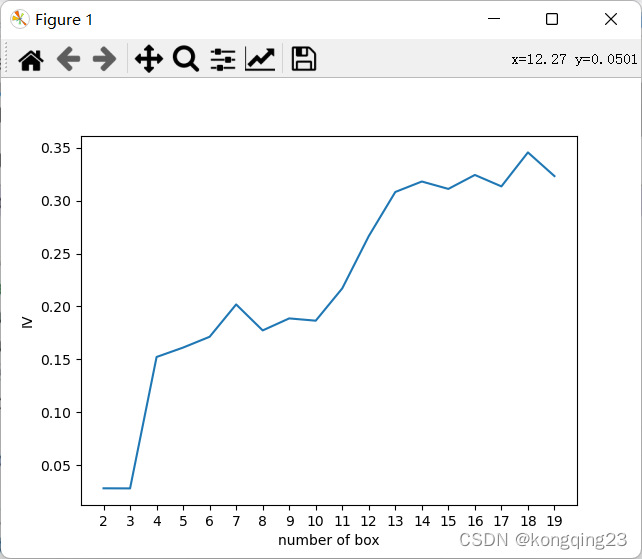
?针对于age而言,选择箱子数据为13比较合适。
import pandas as pd
import numpy as np
import scipy
import matplotlib.pyplot as plt
import imblearn #imblearn是专门用来处理不平衡数据集的库,在处理样本不均衡问题中性能高过sklearn很多
from sklearn.linear_model import LogisticRegression as LR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import train_test_split
from imblearn.over_sampling import SMOTE #从上采样导入smote方法
def fill_missing_rf(X,y,to_fill):
"""
使用随机森林填补一个特征的缺失值的函数
参数:
X:要填补的特征矩阵
y:完整的,没有缺失值的标签
to_fill:字符串,要填补的那一列的名称
返回值:
对缺失值的填补
"""
#构建新的特征矩阵和新标签
df=X.copy()
fill=df.loc[:,to_fill]
df=pd.concat([df.loc[:,df.columns != to_fill],pd.DataFrame(y)],axis=1) #将特征矩阵中不需要填充的部分和完整的标签做左右拼接
#找出随机森林的训练集 测试集
Ytrain=fill[fill.notnull()]
Ytest=fill[fill.isnull()]
Xtrain=df.iloc[Ytrain.index,:]
Xtest=df.iloc[Ytest.index,:]
#利用随机森林填补缺失值
rfr = RFR(n_estimators=100)
rfr = rfr.fit(Xtrain, Ytrain)
Ypredict = rfr.predict(Xtest)
return Ypredict
def graphforbestbin(DF, X, Y, n=5,q=20,graph=True):
"""
自动最优分箱函数,基于卡方检验的分箱
参数:
DF: 需要输入的数据
X: 需要分箱的列名
Y: 分箱数据对应的标签 Y 列名
n: 保留分箱个数
q: 初始分箱的个数
graph: 是否要画出IV图像
区间为前开后闭 (]
"""
DF = DF[[X,Y]].copy()
#分箱
DF["qcut"],bins = pd.qcut(DF[X], retbins=True, q=q,duplicates="drop")
coount_y0 = DF.loc[DF[Y]==0].groupby(by="qcut").count()[Y]#统计对应列结果为0的个数
coount_y1 = DF.loc[DF[Y]==1].groupby(by="qcut").count()[Y]#统计对应列结果为1的个数
num_bins = [*zip(bins,bins[1:],coount_y0,coount_y1)] #创建箱子列表 下限 上限 0的个数 1的个数
for i in range(q):
#如果第一个组没有包含正样本或负样本,向后合并
if 0 in num_bins[0][2:]:
num_bins[0:2] =[(num_bins[0][0],
num_bins[1][1],
num_bins[0][2]+num_bins[1][2],
num_bins[0][3]+num_bins[1][3])]
continue
#已经确认第一组中肯定包含两种样本了,如果其他组没有包含两种样本,就向前合并
#此时的num_bins已经被上面的代码处理过,可能被合并过,也可能没有被合并
#但无论如何,我们要在num_bins中遍历,所以写成in range(len(num_bins))
for i in range(len(num_bins)):
if 0 in num_bins[i][2:]:
num_bins[i-1:i+1] = [(num_bins[i-1][0],
num_bins[i][1],
num_bins[i-1][2]+num_bins[i][2],
num_bins[i-1][3]+num_bins[i][3])]
#即一旦合并发生,我们就让循环被破坏,使用break跳出当前循环
break
else:
break
#计算WOE和BAD RATE
#BAD RATE与bad%不是一个东西
#BAD RATE是一个箱中,坏的样本所占的比例 (bad/total)
#而bad%是一个箱中的坏样本占整个特征中的坏样本的比例
def get_woe(num_bins):
# 通过 num_bins 数据计算 woe
columns = ["min","max","count_0","count_1"]
df = pd.DataFrame(num_bins,columns=columns)
df["total"] = df.count_0 + df.count_1
df["percentage"] = df.total / df.total.sum()
df["bad_rate"] = df.count_1 / df.total
df["good%"] = df.count_0/df.count_0.sum()
df["bad%"] = df.count_1/df.count_1.sum()
df["woe"] = np.log(df["good%"] / df["bad%"])
return df
#计算IV值
def get_iv(df):
rate = df["good%"] - df["bad%"]
iv = np.sum(rate * df.woe)
return iv
IV = []#IV得分
axisx = []#箱子个数 画图时用作横坐标
while len(num_bins) > n:
pvs = []
for i in range(len(num_bins)-1):
x1 = num_bins[i][2:]
x2 = num_bins[i+1][2:]
pv = scipy.stats.chi2_contingency([x1,x2])[1]
pvs.append(pv)
#通过p值进行处理 合并p值最大的两组
#合并两个箱子时 取第一个箱子的下限 第二个箱子的上限 将两个箱子内0的值 1的值相加
i=pvs.index(max(pvs))
num_bins[i:i+2]=[(num_bins[i][0],
num_bins[i+1][1],
num_bins[i][3]+num_bins[i+1][3],
num_bins[i][2]+num_bins[i+1][2])]
bins_df = pd.DataFrame(get_woe(num_bins))
axisx.append(len(num_bins))
IV.append(get_iv(bins_df))
#画图
if graph:
plt.figure()
plt.plot(axisx,IV)
plt.xticks(axisx)
plt.xlabel("number of box")
plt.ylabel("IV")
plt.title(X)
plt.show()
return pd.DataFrame(get_woe(num_bins))
#df是表格,col是需要进行计算woe的特征,y是标签,bins是分箱的各个界限区间
def get_woe(df,col,y,bins):
#bins是分箱的左右端点
#cut是按照自己设定的进行分箱,qcut是等频分箱
df = df[[col,y]].copy()
df['cut'] = pd.cut(df.loc[:,col],bins)
bins_df = df.groupby('cut')[y].value_counts().unstack()
woe = np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum()))
df['woe'] = woe
return woe
data=pd.read_csv('rankingcard.csv',index_col=0)#不额外添加列
#查看数据
# print(data.head())
# print(data.info())
# print(data.shape) #10个特征 第一列为是否会违约(结果)
#删除重复的数据
data.drop_duplicates(inplace=True)#inplace=true表示直接对原数据进行操作
data.index=range(data.shape[0]) #删除重复数据以后 一定要恢复索引
#填补缺失值
# print(data.isnull().sum()/data.shape[0]) #查看缺失数据比率
#也可以这样写
# print(data.isnull().mean())
#使用均值填补家属人数
data['NumberOfDependents'].fillna(int(data['NumberOfDependents'].mean()),inplace=True)
#使用随机森林填补月收入缺失
X=data.iloc[:,1:]
y=data['SeriousDlqin2yrs']
y_pred=fill_missing_rf(X,y,'MonthlyIncome')
data.loc[data.loc[:,'MonthlyIncome'].isnull(),'MonthlyIncome']=y_pred
#print(data.isnull().mean()) #检测填充是否成功
#描述性统计处理异常值
data.describe([0.01,0.1,0.25,.5,.75,.9,.99]).T
#异常值也被我们观察到,年龄的最小值居然有0,这不符合银行的业务需求,
# 即便是儿童账户也要至少8岁,我们可以查看一下年龄为0的人有多少
data = data[data["age"] != 0] #删除年龄为0的用户
data = data[data.loc[:,"NumberOfTimes90DaysLate"] < 90]#不阔能超过90次
data.index=range(data.shape[0])#更新索引
#删除了异常值后的数据
X1=data.iloc[:,1:]
y1=data.iloc[:,0]
n_sample=X1.shape[0]#样本数量
n_1_sample = y.value_counts()[1]#结果为1数量
n_0_sample = y.value_counts()[0]#结果为0数量
# print('样本个数:{}; 1占{:.2%}; 0占{:.2%}'.format(n_sample,n_1_sample/n_sample,n_0_sample/n_sample))
#处理样本不平衡问题
sm=SMOTE()
X1,y1=sm.fit_resample(X1,y1)
n_sample_ = X1.shape[0]
n_1_sample = pd.Series(y1).value_counts()[1]
n_0_sample = pd.Series(y1).value_counts()[0]
# print('上采样后样本个数:{}; 1占{:.2%}; 0占{:.2%}'.format(n_sample_,n_1_sample/n_sample_,n_0_sample/n_sample_))
#分训练集和测试集并保存
X1=pd.DataFrame(X1)
y1=pd.DataFrame(y1)
X_train, X_vali, Y_train, Y_vali = train_test_split(X1,y1,test_size=0.3,random_state=420)
#训练数据 特征矩阵第一列设为标签
model_data = pd.concat([Y_train, X_train], axis=1)
model_data.index = range(model_data.shape[0]) #更新索引
model_data.columns = data.columns #更新列索引
#验证数据 特征矩阵第一列设为标签
vali_data = pd.concat([Y_vali, X_vali], axis=1)
vali_data.index = range(vali_data.shape[0])
vali_data.columns = data.columns
#导出文件
model_data.to_csv("model_data.csv")
vali_data.to_csv("vali_data.csv")
#可以自动分箱的特征
auto_col_bins = {"RevolvingUtilizationOfUnsecuredLines":6,
"age":5,
"DebtRatio":4,
"MonthlyIncome":3,
"NumberOfOpenCreditLinesAndLoans":5}
#不能使用自动分箱的变量
hand_bins = {"NumberOfTime30-59DaysPastDueNotWorse":[0,1,2,13]
,"NumberOfTimes90DaysLate":[0,1,2,17]
,"NumberRealEstateLoansOrLines":[0,1,2,4,54]
,"NumberOfTime60-89DaysPastDueNotWorse":[0,1,2,8]
,"NumberOfDependents":[0,1,2,3]}
#保证区间覆盖使用 np.inf替换最大值,用-np.inf替换最小值
#原因:比如一些新的值出现,例如家庭人数为30,以前没出现过,改成范围为极大值之后,这些新值就都能分到箱里边了
hand_bins = {k:[-np.inf,*v[:-1],np.inf] for k,v in hand_bins.items()}
#分箱的左右端点
bins_of_col = {}
for col in auto_col_bins:
bins_df = graphforbestbin(model_data,col
,'SeriousDlqin2yrs'
#使用字典的性质来取出每个特征所对应的箱的数量
,n=auto_col_bins[col]
,q=20,graph=False)
#将min和max转为集合,union是取两个集合的并集,bins_list就是各个区间的端点
bins_list = sorted(set(bins_df["min"]).union(bins_df["max"]))
#保证区间覆盖使用 np.inf 替换最大值 -np.inf 替换最小值
bins_list[0],bins_list[-1] = -np.inf,np.inf
bins_of_col[col] = bins_list
#合并手动分箱数据 ,将hand_bins所有的键值对更新到bins_of_col字典里
bins_of_col.update(hand_bins)
data = model_data.copy()
#将所有特征的WOE存储到字典当中
woeall = {}
for col in bins_of_col:
woeall[col] = get_woe(model_data,col,"SeriousDlqin2yrs",bins_of_col[col])
#不希望覆盖掉原本的数据,创建一个新的DataFrame,索引和原始数据model_data一模一样
model_woe = pd.DataFrame(index=model_data.index)
#对所有特征操作可以写成:
for col in bins_of_col:
model_woe[col] = pd.cut(model_data.loc[:,col],bins_of_col[col]).map(woeall[col])
#将标签补充到数据中
model_woe['SeriousDlqin2yrs'] = model_data['SeriousDlqin2yrs']
#这就是我们的建模数据了
model_woe.head()
#导入测试集
vail_data = pd.read_csv('vali_data.csv',index_col=0)
vail_woe = pd.DataFrame(index=vail_data.index)
for col in bins_of_col:
vail_woe[col] = pd.cut(vail_data.loc[:,col],bins_of_col[col]).map(woeall[col])
vail_woe["SeriousDlqin2yrs"] = vail_data["SeriousDlqin2yrs"]
#对训练集和测试集的特征和标签分离
x = model_woe.iloc[:,:-1]
y = model_woe.iloc[:,-1]
vail_x = vail_woe.iloc[:,:-1]
vail_y = vail_woe.iloc[:,-1]
lr = LR().fit(x,y)
print(lr.score(vail_x,vail_y))