1.Hough Transform
https://homepages.inf.ed.ac.uk/rbf/HIPR2/hough.htm
霍夫变换于1962年由Paul Hough首次提出,后于1972年由Richard Duda和Peter Hart推广使用,经典霍夫变换用来检测图像中的直线,后来霍夫变换扩展到任意形状物体的识别,多为圆和椭圆。
霍夫变换的原理是将直线 y = k x + b y=kx+b y=kx+b上的点变换到极坐标系下 r = x c o s θ + y s i n θ r=xcos\theta+ysin\theta r=xcosθ+ysinθ。
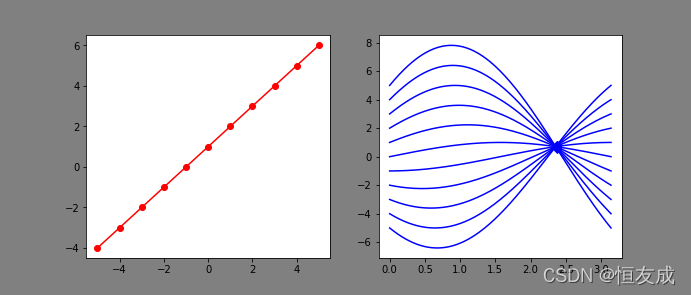
直线 y = k x + b y=kx+b y=kx+b上的点 p 1 ( x 1 , y 1 ) , p 2 ( x 2 , y 2 ) . . . p n ( x n , y n ) p_1(x_1, y_1),p_2(x_2, y_2) ... p_n(x_n, y_n) p1?(x1?,y1?),p2?(x2?,y2?)...pn?(xn?,yn?)在极坐标系下可得对应的曲线方程 r = x 1 c o s θ + y 1 s i n θ , r = x 2 c o s θ + y 2 θ r=x_1cos\theta+y_1sin\theta,r=x_2cos\theta+y_2\theta r=x1?cosθ+y1?sinθ,r=x2?cosθ+y2?θ等,画出以 p 1 , p 2 , . . . , p n p_1,p_2,...,p_n p1?,p2?,...,pn?等为系数的方程在 θ ∈ [ 0 , π ] \theta\in[0,\pi] θ∈[0,π]上的曲线,这些曲线将相交于一点,这个相交点 ( θ 0 , r 0 ) (\theta_0,r_0) (θ0?,r0?)即表示直线与x轴的夹角和直线到原点的距离。
使用霍夫变换检测直线时只需要找到极坐标系中曲线的交点即可找到图像中的直线。
r
=
x
c
o
s
θ
+
y
s
i
n
θ
r=xcos\theta+ysin\theta
r=xcosθ+ysinθ类似于
A
x
+
B
y
+
C
=
0
Ax+By+C=0
Ax+By+C=0,因为
p
1
,
p
2
p_1, p_2
p1?,p2?共线,因此存在ABC满足一次多元方程的解,即为极坐标系中的交点
(
r
,
θ
)
(r, \theta)
(r,θ)
概率霍夫变换:
[156] Jiri Matas, Charles Galambos, and Josef Kittler. Robust detection of lines using the progressive probabilistic hough transform. Computer Vision and Image Understanding, 78(1):119–137, 2000.
引用自
概率霍夫变换(Progressive Probabilistic Hough Transform)的原理很简单,如下所述:
1).随机获取边缘图像上的前景点,映射到极坐标系画曲线;
2).当极坐标系里面有交点达到最小投票数,将该点对应x-y坐标系的直线L找出来;
3).搜索边缘图像上前景点,在直线L上的点(且点与点之间距离小于maxLineGap的)连成线段,然后这些点全部删除,并且记录该线段的参数(起始点和终止点),当然线段长度要满足最小长度;
4).重复1). 2). 3).
同样的思想可以用到其他多边形上,例如霍夫圆检测,与使用 ( ρ , θ ) (\rho, \theta) (ρ,θ)表示一条直线类似,可以使用 ( a , b , r ) (a,b,r) (a,b,r)表示圆心为 ( a , b ) (a,b) (a,b)半径为 r r r的圆,以 a , b , r a,b,r a,b,r为参数,在3d空间上画曲线,则图像中在同一个圆的点所对应的曲线将相交于1点,该点即对应图像中圆的参数。
这种方法计算量巨大。速度很慢,opencv中使用的是较简便的算法。OpenCV实现的是一个比标准霍夫圆变换更为灵活的检测方法——霍夫梯度法,该方法运算量相对于标准霍夫圆变换大大减少。其检测原理是依据圆心一定是在圆上的每个点的模向量上,这些圆上点模向量的交点就是圆心,霍夫梯度法的第一步就是找到这些圆心,这样三维的累加平面就又转化为二维累加平面。第二步是根据所有候选中心的边缘非0像素对其的支持程度来确定半径。参考
霍夫梯度法原理介绍:
- 首先对图像进行边缘检测,(Canny)
- 然后对边缘图像中的非零点考虑局部梯度(Sobel)
- 这个梯度即直线的斜率,沿着这个斜率表示的直线在累加器内从一个较小值移动到较大值,同时记录轮廓图像中每个非零像素点的位置
- 将这些非零像素点根据其累加器中的值降序排列,取大于阈值点,找到最有可能是圆心的点
- 对于每个圆心考虑所有非零像素点,将这些像素根据距圆心的距离排序, 从最小距离到最大距离中,选最好的值作为半径
- 若有足够数量的点组合成一个 圆并且其圆心与之前选中的圆心距离足够大就保留这个圆心
2.OpenCV API
2.1霍夫线检测
霍夫线变换的直接输入只能是边缘二值图像。
OpenCV中有俩个霍夫直线检测的API,
-
标准方法:
HoughLines()返回 ( θ , r θ ) (\theta, r_{\theta}) (θ,rθ?)void cv::HoughLines ( InputArray image, OutputArray lines, double rho, double theta, int threshold, double srn = 0, double stn = 0, double min_theta = 0, double max_theta = CV_PI )- image单通道8位图像
- lines表示直线的向量,
Vec2f( ρ , θ ) \rho,\theta) ρ,θ) - ρ \rho ρ轴的精度,单位是像素
- θ \theta θ轴的精度,单位是弧度
- threshold累积的投票阈值,在极坐标系中曲线交点的个数大于阈值才认为是有直线
-
更高效的随机方法:
HoughLinesP()返回线段的两端, ( x 0 , y 0 , x 1 , y 1 ) (x_0, y_0, x_1, y_1) (x0?,y0?,x1?,y1?)void cv::HoughLinesP ( InputArray image, OutputArray lines, double rho, double theta, int threshold, double minLineLength = 0, double maxLineGap = 0 )minLineLength线的最短长度,比minLineLength短的线将被舍弃,单位像素maxLineGap,同一条直线上两点的最大允许距离,单位像素
#include <opencv2/imgcodecs.hpp>
#include <opencv2/imgproc.hpp>
#include <opencv2/highgui.hpp>
#include <iostream>
#include <vector>
using namespace std;
int main(int argc, char **argv)
{
cv::Mat dst, cdst, cdstP;
const char *default_filename = "/home/lx/CLionProjects/LearnOpenCv/imgs/line.png";
const char *filename = argc >= 2 ? argv[1] : default_filename;
cv::Mat src = cv::imread(cv::samples::findFile(filename), cv::IMREAD_GRAYSCALE);
if(src.empty())
{
std::cout << filename << "is empty." << std::endl;
return -1;
}
// Edge detection
Canny(src, dst, 50, 200, 3);
cv::imshow("canny result", dst);
// Copy edges to the images that will display the results in BGR
cvtColor(dst, cdst, cv::COLOR_GRAY2BGR);
// cv::erode(dst, dst, cv::getStructuringElement(cv::MORPH_CROSS, cv::Size(2, 2)));
// cv::imshow("Erode Image:", dst);
cdstP = cdst.clone();
// Standard Hough Line Transform
vector<cv::Vec2f> lines;
cv::HoughLines(dst, lines, 1, CV_PI/180, 100, 0, 0);
// draw the lines
std::cout << "Standard Detected Line Numbers: " << lines.size() << std::endl;
for(int i = 0; i < lines.size(); i++)
{
float rho = lines[i][0];
float theta = lines[i][1];
cv::Point p1, p2;
double a = cos(theta);
double b = sin(theta);
double x0 = rho * a;
double y0 = rho * b;
p1.x = cvRound(x0 + 1000*(-b));
p1.y = cvRound(y0 + 1000*a);
p2.x = cvRound(x0 - 1000*(-b));
p2.y = cvRound(y0 - 1000*a);
cv::line(cdst, p1, p2, cv::Scalar(0, 0, 255), 3, cv::LINE_AA);
}
cv::imwrite("std_line_res.png", cdst);
vector<cv::Vec4f> linesP;
cv::HoughLinesP(dst, linesP, 1, CV_PI/180, 2, 2, 5);
std::cout << "Probabilistic Detected Line Numbers: " << linesP.size() << std::endl;
for(int i = 0; i < linesP.size(); i++)
{
cv::Vec4f l = linesP[i];
cv::line(cdstP, cv::Point(l[0], l[1]), cv::Point(l[2, l[3]]), cv::Scalar(0, 0, 255), 3, cv::LINE_AA);
}
cv::imwrite("prob_line_res.png", cdstP);
imshow("Source", src);
imshow("Detected Lines (in red) - Standard Hough Line Transform", cdst);
imshow("Detected Lines (in red) - Probabilistic Line Transform", cdstP);
// Wait and Exit
cv::waitKey();
return 0;
}
结果:
原图

标准霍夫变换直线检测

2.2霍夫圆检测
- HoughCircles
void cv::HoughCircles( InputArray image, OutputArray circles, int method, double dp, double minDist, double param1 = 100, double param2 = 100, int minRadius = 0, int maxRadius = 0 )image:8位单通道灰度图circles检测到的圆,结果为Vec3f或Vec4f,分别表示 ( x , y , r a d i u s ) (x, y, radius) (x,y,radius), ( x , y , r a d i u s , v o t e s ) (x, y, radius, votes) (x,y,radius,votes)method检测方法,当前仅支持HOUGH_GRADIENTdp累加器的精度,1表示与输入图像的分辨率相同,2表示累加器的分辨率是原图的一半,依次类推minDist检测圆的中心的最小距离,小于此距离的圆将被忽略param1第一个根据method而适配的参数,method为HOUGH_GRADIENT时,其表示边缘检测算法Canny中较大的那个参数,Canny算法中另一个较小的参数是该值的1/2param2第二个根据method而适配的参数,method为HOUGH_GRADIENT时,它是检测阶段确定圆心个数的阈值,该值越小,圆检测的召回率就越高,准确率越低minRadius检测的最小的圆的直径maxRadius检测的最大的圆的直径
例子:
#include <opencv2/imgcodecs.hpp>
#include <opencv2/imgproc.hpp>
#include <opencv2/highgui.hpp>
#include <iostream>
#include <vector>
using namespace std;
int main(int argc, char **argv)
{
const char* filename = argc >=2 ? argv[1] : "apple.png";
// Loads an image
cv::Mat src = cv::imread( cv::samples::findFile( filename ), cv::IMREAD_COLOR );
// Check if image is loaded fine
if(src.empty()){
printf(" Error opening image\n");
printf(" Program Arguments: [image_name -- default %s] \n", filename);
return EXIT_FAILURE;
}
cv::Mat gray;
cv::cvtColor(src, gray, cv::COLOR_BGR2GRAY);
cv::medianBlur(gray, gray, 5);
vector<cv::Vec4f> circles;
long t1 = cv::getTickCount();
cv::HoughCircles(gray, circles, cv::HOUGH_GRADIENT, 1, 100, 30, 1, 10);
cout << "Time Used: " << cv::getTickCount() - t1 << endl;
t1 = cv::getTickCount();
cv::HoughCircles(gray, circles, cv::HOUGH_GRADIENT, 4, 100, 30, 1, 10);
cout << "Time Used: " << cv::getTickCount() - t1 << endl;
for(size_t i=0; i < circles.size(); i++)
{
cv::Vec4i c = circles[i];
cv::Point center;
center.x = c[0];
center.y = c[1];
cv::circle(src, center, 2, cv::Scalar(0, 0, 255), 2);
int r = c[2];
cv::circle(src, center, r, cv::Scalar(0, 0, 255), 3, cv::LINE_AA);
cout << "circle vote numbers: " << c[3] << std::endl;
}
cv::imwrite("detected_circle.png", src);
cv::imshow("detected circles", src);
cv::waitKey();
return 0;
}
原图:

结果:

参数dp从1调到4后,累加器变小,圆检测需要的时间确实变小了
Time Used: 44.367 ms
Time Used: 7.93723 ms
circle vote numbers: 104