[人工智能]基于SVM(支持向量机)对鸢尾花进行分类

支持向量机方法也是一种强大的机器学习分类方法。
在感知器算法中，我们的目标是最小化分类误差，而在SVM中，我们的优化目标是最大化分类间隔。
较大的分类间隔意味着模型有较小的泛化误差，较小的间隔则意味着模型可能会过拟合。
在SVM中的两条平行的决策边界为：
$$w_0+{\mathbf{w}}^T{\mathbf{x}}_{pos}=1$$
$$w_0+{\mathbf{w}}^T{\mathbf{x}}_{neg}=?1$$
两式相减可得：
$${\mathbf{w}}^T({\mathbf{x}}_{pos}?{\mathbf{x}}_{neg})=2$$
定义
$$||\mathbf{w}||=\sqrt{\sum _{j=1}^m{w}_j^2}$$
可得
$$\frac{{\mathbf{w}}^T({\mathbf{x}}_{pos}?{\mathbf{x}}_{neg})}{||\mathbf{w}||}=\frac{2}{||\mathbf{w}||}$$
等式左侧为正负超平面间的距离，也就是所要最大化的间隔，故需使$2/||\mathbf{w}||$最大。
SVM的目标函数记为：
$$w_0+{\mathbf{w}}^T{\mathbf{x}}^i\ge 1,\text{if}{y}^{(i)}=1$$
$$w_0+{\mathbf{w}}^T{\mathbf{x}}^i\le 1,\text{if}{y}^{(i)}=?1$$
对于非线性可分的数据，需要放松线性约束条件，以保证在适当的罚项成本下，对错误的分类情况优化时能够收敛。
$$w_0+{\mathbf{w}}^T{\mathbf{x}}^i\ge 1,\text{if}{y}^i=1?{\xi }^{(i)}$$
$$w_0+{\mathbf{w}}^T{\mathbf{x}}^i\le 1,\text{if}{y}^i=?1+{\xi }^{(i)}$$
通过引入$C$值，新的目标优化为使下式最小：
$$\frac{1}{2}||\mathbf{w}|{|}^2+C(\sum _i{\xi }^{(i)})$$
通过这种方法我们也可以对鸢尾花进行分类，代码引自《python机器学习》

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import numpy as np
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3,random_state=0)

sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std: object = sc.transform(X_test)


def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
    # 设置marker generator和color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim = (xx2.min(), xx2.max())
    X_test, y_test = X[test_idx, :], y[test_idx]
    for idx, cl in enumerate(np.unique(y)):  # np.unique:去除重复数据
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl)
    if test_idx:
        X_test, y_test = X[test_idx, :], y[test_idx]
        plt.scatter(X_test[:, 0], X_test[:, 1], c='black', alpha=0.8, linewidths=1, marker='o', s=10, label='test set')


X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
svm = SVC(kernel='linear', C=1.0, random_state=0)# 使用线性核函数，设置C值为1
svm.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105,150))
plt.xlabel('petal length {standardized}')
plt.ylabel('petal width {standardized}')
plt.legend(loc='upper left')
plt.show()

小黑点表示测试集数据，分类结果如下：

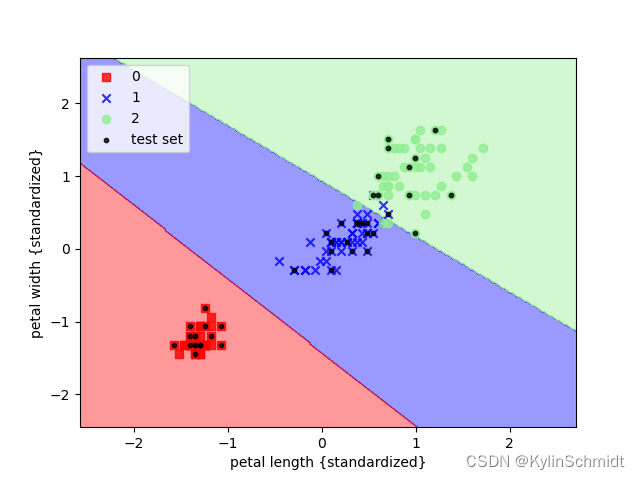
可以观察到分类结果较好。