正则化
引入
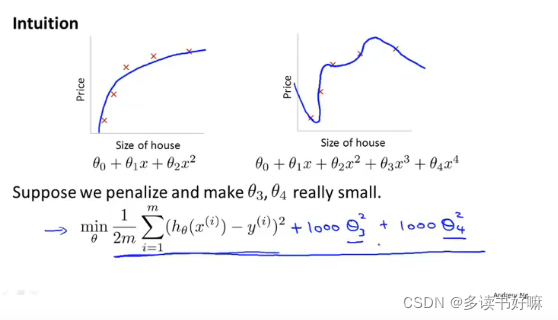
两图都是较好的拟合结果,之前提过P2出现过拟合的情况,泛化的能力不佳。这时为了减小x ^3与x ^4的影响,可以在代价函数中加入惩罚,即图中的形式,+1000θ ^3+1000θ ^4,这样可让两个参数很小
此处的1000指很大的数
正则化思想

简化假设模型,因此也减少了过拟合的情况。
当我们有多个参数,
正则化代价函数
当我们有多个参数,而不知道那些需要添加惩罚,就对所有特征添加惩罚,则可以得到以下正则化代价函数:
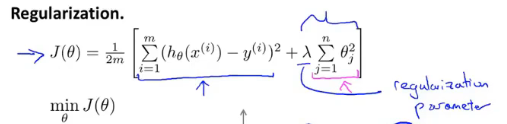
第一项的目的是训练模型更好拟合训练集;第二项目的是保持参数尽可能小,其中从θ0开始累加对结果无影响。
λ:正则化参数,控制两个目标之间的平衡关系

如果对所有特征的惩罚过大(λ过大),则会导致除θ0外的参数趋0,拟合的曲线为直线,会出现欠拟合的情况。
线性回归正则化
梯度下降
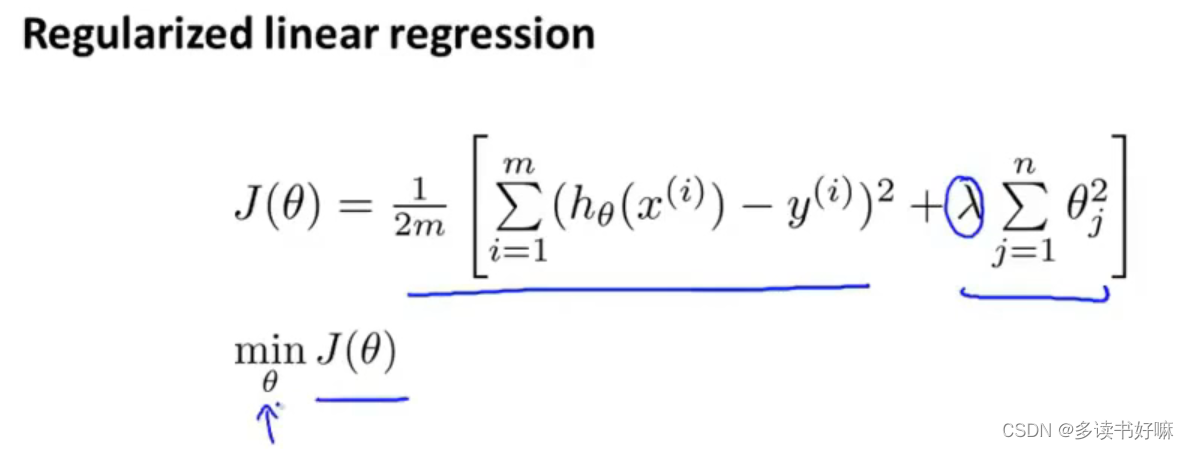
步骤
θ0不参与惩罚

下标非0项也可以写成
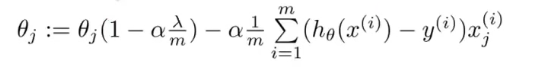
其中θj的系数通常只是略小于1,第二项与之前提到的梯度下降形式一样
正规方程

形式与之前提到类似,加入了一个n+1维的方阵,并且相加后的方阵一定可逆。
逻辑回归正则化
逻辑回归在加入惩罚后的代价函数
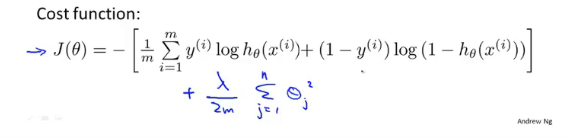
梯度下降
步骤
形式与上文的相同

高级优化算法
代码实现
对于这些算法,我门只需要自己定义一个costFunction 函数,在运行时调用库里有的算法函数即可,如fminuc函数。
