[人工智能]《Enforcing geometric constraints of virtual normal for depth prediction》论文笔记

参考代码：VNL_Monocular_Depth_Prediction

1. 概述

介绍：这篇文章为深度估计提供了一种新的损失函数形式，在深度估计任务中常见的损失函数多以pixel-wise监督的形式出现，因此这些监督损失函数都是利用像素层面的浅层信息进行监督约束的。这样的浅层次深度信息学习自然不能很好学习到GT深度中的一些细节与结构差异信息，因而这篇文章提出将预测深度通过预先假定的相机内参映射到同一模拟空间尺度（3D空间）上进行比较。这里的比较是通过在模拟空间上进行采样，每个采样包含3个点，并通过文章设定的2个采样准则排除无效采样，从而构建预测深度与GT深度的约束。正因为文章的方法是在3D空间进行采样这样使得文章的方法得到的深度更加符合GT在3D空间的分布，也使得深度更加准确。

将GT、文章方法预测深度、其它方法预测深度在点云和surface normal维度进行比较，见下图：

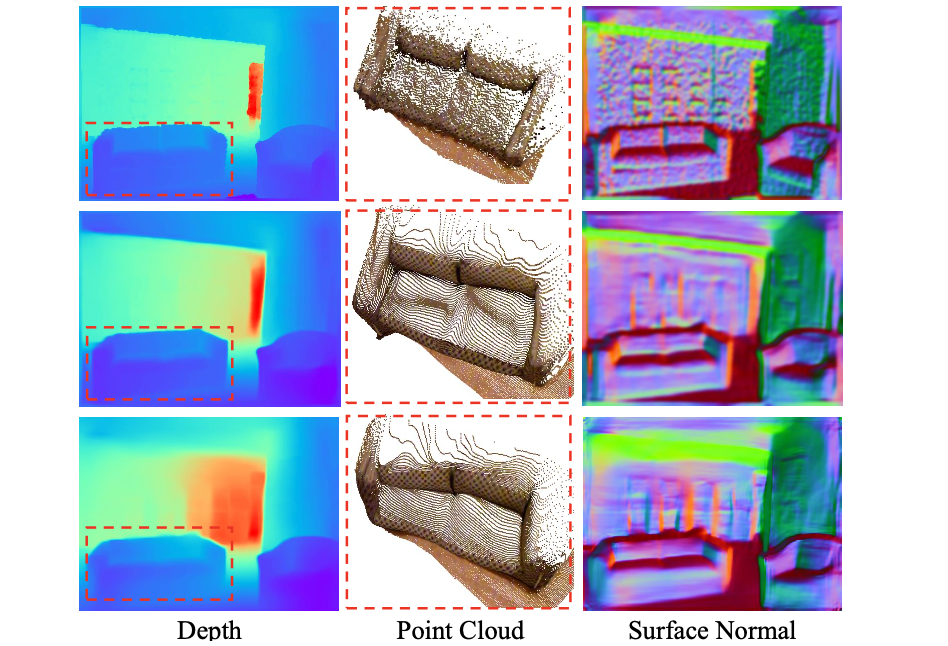
可以看到在surface normal和深度表现差异不是很大的情况下，点云的分布差异更大，因而在点云对应的3D空间进行约束能够得到更加准确的深度。

2. 方法设计

2.1 整体pipeline

这里使用的网络是编解码网络构建的深度预测网络，主要的改进点便是其使用文章中提出的virtual mormal损失函数（也就是在3D空间上建立约束），如下图所示：

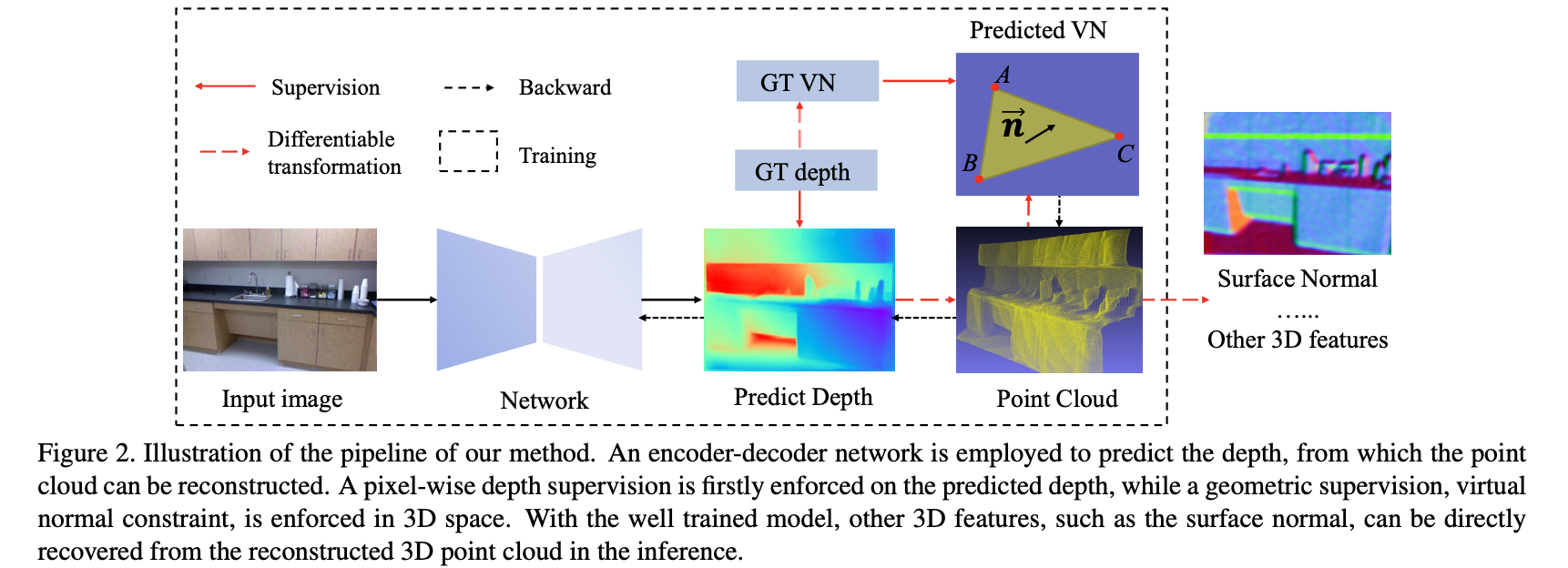
在文章《DiverseDepth: Affine-invariant Depth Prediction Using Diverse Data
》中对深度回归所使用到的损失函数进行了梳理，将其大致分为如下3个类别，而文章的方法virtual normal与surface normal共同属于affine-invariant的，见引用论文中的表2：

这篇文章也将virtual normal与surface normal进行了比较，其指出surface normal的值与local size是存在较大关联的，而且受其影响很大，导致local size的选择会给网络训练带来较大不稳定因素。反观virtual normal使用的3D空间上采样的形式进行约束，其会更加鲁棒和稳定一些。

2.2 virtual normal损失

virtual normal损失是在3D空间上通过采样的方式选择满足文章条件的点，并且构建对应向量空间，并比较向量空间上的差异，其实现可以参考文章代码：VNL_loss.py。

这里假设焦距为$f_x,f_y$，当前像素点与深度值分别为$(u_i,v_i),d_i$，当前图像的中心点$(u_0,v_0)$，则可以将图像坐标映射到相机坐标下：
$$z_i=d_i;x_i=\frac{d_i?(u_i?u_0)}{f_x};y_i=\frac{d_i(v_i?v_0)}{f_y}$$
对于3D空间上的采样点集合 s = { ( P A , P B , P C ) o ∣ i = 0 , … , N } \mathcal{s}=\{(P_A,P_B,P_C)_o|i=0,\dots,N\} s={(PA?,PB?,PC?)o?∣i=0,…,N}是通过设置2个采样准则的方式实现：不共线准则与远距离准则。

不共线准则：
这里需要满足样本点不再同一条直线上，则对应采样点之间组成的向量满足余弦准则：
R 1 = { α ≥ ∠ ( P A P B → , P A P C → ) ≥ β , ? α ≥ ∠ ( P B P C → , P B P A → ) ≥ β ∣ P ∈ s } \mathcal{R}_1=\{\alpha\ge\angle(\overrightarrow{P_AP_B},\overrightarrow{P_AP_C})\ge\beta,\ \alpha\ge\angle(\overrightarrow{P_BP_C},\overrightarrow{P_BP_A})\ge\beta|P\in\mathcal{s}\} R1?={α≥∠(PA?PB? ?,PA?PC? ?)≥β,?α≥∠(PB?PC? ?,PB?PA? ?)≥β∣P∈s}
其对应的代码可以参考：

nm = torch.bmm(q_norm.view(m_batchsize * groups, index, 1), q_norm.view(m_batchsize * groups, 1, index))  # 计算两个向量的模的乘积
energy = torch.bmm(proj_query, proj_key)  # 两个向量乘积
norm_energy = energy / (nm + 1e-8)  # 计算余弦值
mask_cos = torch.sum((norm_energy > delta_cos) + (norm_energy < -delta_cos), 1) > 3  # 筛选满足角度要求的采样

远距离准则：
这里为了防止采样的点过于靠近这里使用一个距离阈值作为筛选准则，其筛选准则为：
R 2 = { ∣ ∣ P k P m → ∣ ∣ > θ ∣ k , m ∈ [ A , B , C ] , P ∈ s } \mathcal{R}_2=\{||\overrightarrow{P_kP_m}||\gt\theta|k,m\in[A,B,C],P\in\mathcal{s}\} R2?={∣∣Pk?Pm? ?∣∣>θ∣k,m∈[A,B,C],P∈s}
其中的参数$\theta$就是选定的距离阈值，其对应的实现代码参考（delta_diff_*就是对应选择的阈值）：

mask_x = torch.sum(torch.abs(pw_diff[:, :, 0, :]) < delta_diff_x, 2) > 0
mask_y = torch.sum(torch.abs(pw_diff[:, :, 1, :]) < delta_diff_y, 2) > 0
mask_z = torch.sum(torch.abs(pw_diff[:, :, 2, :]) < delta_diff_z, 2) > 0

在通过上述方法选择得到对应的采样之后就需要对这些采样组成的向量进行组合描述，文章选择的表达形式为：
N = { n i = P A i P B i → × P A i P C i → ∣ ∣ P A i P B i → × P A i P C i → ∣ ∣ ∣ ( P A , P B , P C ) i ∈ s , i = 0 , … , N } \mathcal{N}=\{n_i=\frac{\overrightarrow{P_{A_i}P_{B_i}}\times\overrightarrow{P_{A_i}P_{C_i}}}{||\overrightarrow{P_{A_i}P_{B_i}}\times\overrightarrow{P_{A_i}P_{C_i}}||}|(P_A,P_B,P_C)_i\in\mathcal{s},i=0,\dots,N\} N={ni?=∣∣PAi??PBi?? ?×PAi??PCi?? ?∣∣PAi??PBi?? ?×PAi??PCi?? ??∣(PA?,PB?,PC?)i?∈s,i=0,…,N}

扰动鲁棒性分析：
在深度估计的过程中难免会存在扰动的情况，对应的就是下图中的点$P^{{}^{\prime \prime }}$，则这个扰动会给对应表达$n$带来什么样的影响呢？

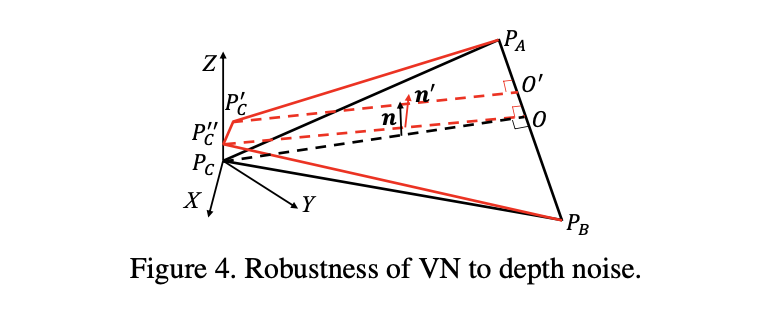
对于带来的扰动可以进行分析：
$$\angle (n,n^{{}^{\prime }})=\angle (O{P}_C,O{P}^{{}^{\prime \prime }})=\arctan \frac{||P_C{P}_C^{{}^{\prime \prime }}||}{||O{P}_C||}\approx 0$$
上面的关系满足是因为在上面提到的采样过过程中对采样的距离做了限制，既是：
$$||P_C{P}_C^{{}^{\prime \prime }}||?||O{P}_C||$$
综上，文章将对应空间上的表达描述为L1损失函数的形式：
$$L_{VN}=\frac{1}{N}(\sum _{i=0}^N||n_i^{pred}?n_i^{gt}|{|}_1)$$

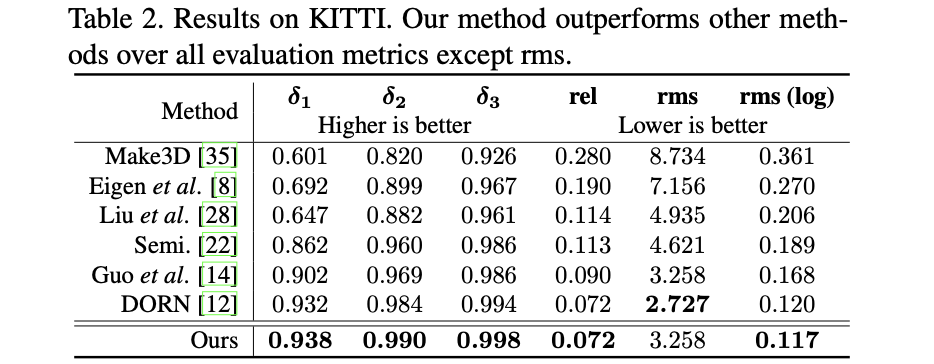
3. 实验结果

NYUD数据集：

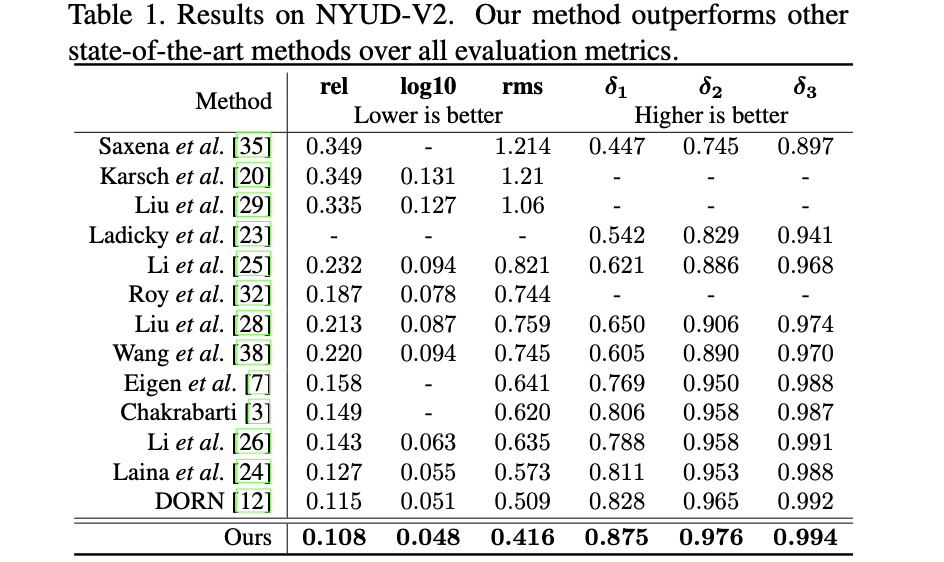
KITTI数据集：