第五章：图信号处理与图卷积神经网络

图信号处理（Graph Signal Processing, GSP）是离散信号处理（Discrete Signal Processing, DSP）理论在图信号领域的应用，其通过对傅里叶变换、滤波等信号处理基本概念的迁移，来研究对图信号的压缩、变换、重构等信号处理的基础任务。

图信号处理与图卷积模型密切相关：

有助于了解图卷积模型的定义和演变
为图卷积模型的理论研究提供工具

本文，首先给出图信号的基本定义，然后介绍图傅里叶变换，并引出图信号频率的定义；然后介绍图信号上的滤波操作，以及卷积滤波与图卷积模型的关系。同时还介绍了对图信号的频域与空域的理解。

1. 矩阵乘法的三种方式

设两个矩阵 $A\in R^{K}$ ， $B\in R^{M\times P}$ ，对于 $C = A B$ ，有如下3种计算方式：

(1)内积视角：将A视作一个行向量矩阵，将B视作一个列向量矩阵，则
$C_{ij}=A_{i,:}B_{:,j}$
(2)行向量视角：将B视作一个行向量矩阵，将A视作系数矩阵，则
$C_{i,:}=\sum_{m}^MA_{im}B_{m,:}$
(3)列向量视角：将A视作一个列向量矩阵，将B视作系数矩阵，则
$C_{:,j}=\sum_{m}^MB_{mj}A_{:,m}$

举例： $A=\begin{bmatrix} 1 & -1 & 2\\ 0 & 2 & 1 \end{bmatrix}$ ， $B=\begin{bmatrix} 2 & 0\\ -1 & 1\\ 0 & -1 \end{bmatrix}$ ，以内积视角计算，可得 $C=\begin{bmatrix} 3 & -3\\ -2 & 1 \end{bmatrix}$ ；

如果用行视角进行计算，以C的第一行计算过程为例：
$\begin{bmatrix} 3 & -3 \end{bmatrix} = \begin{bmatrix} 1 & -1 & 2 \end{bmatrix}\begin{bmatrix} 2 & 0\\ -1 & 1\\ 0 & -1 \end{bmatrix}=1\begin{bmatrix} 2 & 0 \end{bmatrix}+(-1)\begin{bmatrix} -1 & 1 \end{bmatrix}+2\begin{bmatrix} 0 & -1 \end{bmatrix}=[2,0]+[1,-2]+[0,-2]=[3,-3]$
如果用烈士叫进行计算，以C的第一列计算过程为例：
$\begin{bmatrix} 3 \\ -2 \end{bmatrix} = \begin{bmatrix} 1 & -1 & 2\\0 & 2 & 1\end{bmatrix}\begin{bmatrix}2 \\-1 \\0\end{bmatrix}=2\begin{bmatrix}1 \\0\end{bmatrix}+(-1)\begin{bmatrix} -1 \\2\end{bmatrix}+0\begin{bmatrix}2 \\1\end{bmatrix}=\begin{bmatrix}2 \\0\end{bmatrix}+\begin{bmatrix} 1 \\-2\end{bmatrix}+\begin{bmatrix}0 \\0\end{bmatrix}=\begin{bmatrix}3 \\-2\end{bmatrix}$
行视角的计算方式对理解空域图卷积的计算逻辑与意义有很大帮助。

2. 图信号与图的拉普拉斯矩阵

给定图 $G = (V, E)$ ， $V$ 表示图中的节点集合，假设其长度为N，图信号是一种描述 $V\rightarrow R$ 的映射，表示成向量的形式： $x=[x_1,x_2,...,x_N]^T$ ，其中 $x_i$ 表示的是节点 $v_i$ 上的信号强度。如下图所示，其中的竖线长度表示节点上信号值的大小：
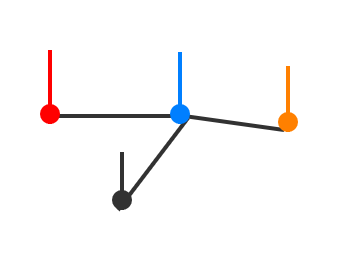
图信号示例
与离散时间信号不同，图信号是定义在节点上的信号，而节点之间有自己固有的关联结构。在研究图信号性质的时候，除了要考虑图信号的强度之外，还需要考虑图的拓扑结构，不同图上同一强度的信号，具有截然不同的性质。

拉普拉斯矩阵（Laplacian Matrix）是用来研究图的结构性质的核心对象，拉普拉斯矩阵的定义如下：
$L = D ? A$
其中，D是一个对角矩阵， $D_{ii}=\sum_jA_{ij}$ 表示的是节点 $v_i$ 的度。拉普拉斯矩阵的元素级别定义如下：
$L_{ij}=\begin{cases} deg(v_i) & \text{ if } i=j \\ -1 & \text{ if } e_{ij}\in E \\ 0 & \text otherwise \end{cases}$

拉普拉斯矩阵还有一种正则化的形式（symmetric normalized laplacian） $L_{sym}=D^{-1/2}LD^{-1/2}$ ，元素级别定义如下：
$L_{sym}[i,j]=\begin{cases} 1 & \text{ if } i=j \\ \frac{-1}{\sqrt{deg(v_i)deg(v_j)}} & \text{ if } e_{ij}\in E \\ 0 & \text otherwise \end{cases}$
注意：这种形式很关键，GCN用的就是这个。

拉普拉斯矩阵的定义来源于拉普拉斯算子，拉普拉斯算子是n维欧式空间种的一个二阶微分算子： $\Delta f=\sum_{i=1}^{n}\frac{\partial^2 f}{\partial x_i^2}$ 。如果将该算子的作用域退化到离散的二维图像空间，就成了边缘检测算子，其作用原理如下：
$\Delta f(x,y)=\frac{\partial^2 f(x,y)}{\partial x^2}+\frac{\partial^2 f(x,y)}{\partial y^2}=[(f(x+1,y)-f(x,y))-(f(x,y)-f(x-1,y))]+[(f(x,y+1)-f(x,y))-(f(x,y)-f(x,y-1))]=[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)]-4f(x,y)$
注：因为是离散的空间，离散函数的导数退化为差分。

在处理图像的时候，上式种的算子会被表示成模板的形式：
$\begin{bmatrix} 0 & 1 & 0\\ 1 & -4 & 1\\ 0 & 1 & 0 \end{bmatrix}$
从模板种可以看出，拉普拉斯算子描述了中心像素与局部上、下、左、右四邻居像素的差异，这种性质通常被用来当作图像上的边缘检测算子。

同理，在图信号中，拉普拉斯算子也被用来描述中心节点与邻居节点之间的信号的差异。如下所示：
$\sum_{v_j\in N(v_i)}(x_i-x_j),...]$
由此可知，拉普拉斯矩阵与图信号相乘后得到的向量中的元素 $L_x)i$ 表示的就是 $v_i$ 的信号值乘以 $v_i$ 的度数再减掉其邻居的信号值之和。所以拉普拉斯矩阵是一个反映图信号局部平滑度的算子。更进一步地，拉普拉斯矩阵可以定义一个非常重要的二次型：
$x^TLx=\sum_{v_i}\sum_{v_j\in N(v_i)}x_i(x_i-x_y)=\sum_{e_{ij}\in E}(x_i-x_j)^2$

令 $TV(x)=x^TLx=\sum_{e_{ij}\in E}(x_i-x_j)^2$ ，称 $T V (x)$ 为图信号的总变差（Total Variation）。总变差是一个标量，它将各条边上信号的差值进行加和，刻画了图信号整体的平滑度。

3. 图傅里叶变换

傅里叶变换是数字信号处理的基石，傅里叶变换将信号从时域空间转换到频域空间，而频域视角给信号的处理带来了极大的便利。例如信号的去噪、压缩、重构等。

图信号傅里叶变换的定义，即将图信号由空域（spatial domain）视角转化到频域（frequency domain）视角，便于图信号处理理论体系的建立。

假设图G的拉普拉斯矩阵为 $L\in R^{N\times N}$ ，由于L是一个实对称矩阵，根据实对称矩阵都可以被正交对角化，可得：
$L=V\Lambda V^T=\begin{bmatrix}... & ... & ... & ...\\v_1 & v_2 & ... & v_N\\ ... & ... & ... & ...\end{bmatrix}\begin{bmatrix} \lambda _1 & & & \\ & \lambda _2 & & \\ & & ... & \\ & & & \lambda _N\end{bmatrix}\begin{bmatrix} ... & v_1 & ...\\... & v_2 & ...\\... & ... & ...\\ ... & v_N & ...\end{bmatrix}$
$V\in R^{N\times N}$ 是一个正交矩阵，即 $VV^T=I\circ V=[v_1,v_2,...,v_N]$ 表示L的N个特征向量，由于V是一个正交矩阵，这些特征向量都是彼此之间线性无关的单位向量。 $\lambda_k$ 表示第k个特征向量对应的特征值，对特征值进行升序排列，即 $\lambda _1 \le \lambda _2 \le...\le \lambda_N$ 。

对于任意给定的向量x，拉普拉斯矩阵的二次型： $x^TLx=\sum_{e_{ij}\in E}(x_i-x_j)^2 \ge 0$ ，因此拉普拉斯矩阵是一个半正定型矩阵，其所有的特征值均大于等于0，即均非负。进一步，由式 $\sum_{v_j\in N(v_i)}(x_i-x_j),...]$ 可知： $L I = 0$ ，因此拉普拉斯矩阵具有最小的特征值0，即 $\lambda_1=0$ 。另外可以证明，对于 $L_{sym}$ ，其特征值存在一个上限： $\lambda_N\le2$ 。

图傅里叶变换（Graph Fourier Transform, GFT）：对于任意一个在图G上的信号x，其图傅里叶变换为：
$\tilde{x_k}=\sum_{i=1}^NV_{ki}^Tx_i=\left \langle v_k, x \right \rangle$
称特征向量为傅里叶基， $\tilde{x_k}$ 是x在第k个傅里叶基上的傅里叶系数。从定义式上可以看出，傅里叶系数本质上是图信号在傅里叶基上的投影，衡量了图信号与傅里叶基之间的相似度。用矩阵形式可计算出所有的傅里叶系数：
$\tilde{x}=V^Tx,\tilde{x}\in R^N$
由于V是一个正交矩阵，对上式左乘V，则： $V\tilde{x}=VV^Tx=Ix=x$ ，即:
$x=V\tilde{x},x\in R^N$

于是，可以将逆图傅里叶变换（Inverse Graph Fourier Transform, IGFT）定义为：
$x_k=\sum_{i=1}^NV_{ki}\cdot \tilde{x_i}$
其中， $x=V\tilde{x},x\in R^N$ 是一种矩阵形式的逆图傅里叶变换，如果将其展开成向量形式，则：
$x=V\tilde{x}=\begin{bmatrix}... & ... & ... & ...\\v_1 & v_2 & ... & v_N\\... & ... & ... & ... \end{bmatrix}\begin{bmatrix}\tilde x_1 \\\tilde x_2 \\... \\\tilde x_N \end{bmatrix}=\tilde x_1v_1+\tilde x_2v_2+...+\tilde x_Nv_N=\sum _{k=1}^N\tilde x_kv_k$
由此可知，从线性代数的角度看，傅里叶基 $v_1,v_2...,v_N$ 组成了N维特征空间中的一组完备的基向量，图G上的任意一个图信号都可以被表征成这些基向量的线性加权。具体地，权重就是图信号在对应傅里叶基上的傅里叶系数，这种对图信号的分解表示方法，给了我们一种全新看待图信号的视角。

图傅里叶变换与图信号的频率有什么关系呢？要理解这个问题，须回到总变差的定义式上，有了图傅里叶变换的定义后，对总变差进行改写：
$TV(x)=x^TLx=x^TV\Lambda V^Tx=(V\tilde x)^TV\Lambda V^T(V\tilde x)=\tilde x^TV^TV\Lambda V^TV\tilde x=\tilde x^T\Lambda \tilde x=\sum_k^N\lambda_k \tilde x_k^2$
从上式中看出，图信号的总变差与图的特征值之间存在着非常直接的线性对应关系，总变差是图的所有特征值的一个线性组合，权重是图信号相对应的傅里叶系数的平方。

问题1：在一个给定的图上，什么样的图信号具有最小的总变差？

将图信号限定在单位向量上来考虑。由于图的各个特征向量是彼此正交的单位向量，且特征值 $\lambda_1,\lambda_2, ...,\lambda_N$ 是从小到大依次排列的，因此总变差取最小值的条件是图信号与最小的特征值 $\lambda_1$ 所对应的特征向量 $v_1$ 完全重合，此时仅有 $x_1\ne0$ ，其他项的傅里叶系数为0，总变差 $TV(v_1)=\lambda_1$ 。事实上，若 $x=v_k$ ，则 $TV(v_k)=\lambda_k$ 。

如果要选择一组彼此正交的图信号，使得各自的总变差依次取得最小值，那么这组图信号就是 $v_1,v_2,...,v_N$ ，如下式：
$\lambda_k=\min_{x:||x||=1,x\perp x_1,x_2,...,x_{k-1}}{x^TLx}$
结合总变差代表着图信号整体平滑度的实际意义，发现特征值依次排列在一起，对图信号的平滑度作出了一种梯度刻画，因此可以将特征值等价成频率。特征值月底，频率越低，对应的傅里叶基就变化得越缓慢，相近节点上得信号值趋于一致；特征值越高，频率越高，对应得傅里叶基就变化得越剧烈，相近节点上得信号值则非常不一致。

问题2：图傅里叶变换到底是个啥？

对图信号进行傅里叶变换：用拉普拉斯矩阵的特征向量作为图傅里叶投影的基。图傅里叶变换并不是通过严谨的数学推导，将傅里叶变换扩展到图上，而是经过许多类比，直接定义成了这个样子。就好像说，傅里叶变换是以拉普拉斯算子的特征向量为基进行投影，那么图傅里叶变换就以拉普拉斯矩阵的特征向量为基进行投影。图傅里叶变换就是在将一个图信号分解到不同平滑程度的图信号上，就像传统傅里叶变换将函数分解到不同频率的函数上一样。

图信号的能量公式：
$E(x)=||x||_2^2=x^Tx=(V\tilde x)^T(V\tilde x)=\tilde x^T \tilde x$
即图信号的能量可以同时从空域和频域进行等价定义。单位向量的图信号能量为1。

有了频率的定义，傅里叶系数就可以等价成图信号在对应频率分量上的幅值，反映了图信号在该频率分量上的强度。图信号的低频分量上的强度越大，该信号的平滑度就越高。相反，则平滑度越低。

定义好图傅里叶变换之后，可以从频域视角去研究图信号了。把图信号所有的傅里叶系数合在一起称为该信号的频谱（spectrum）。在一个给定的图中，图信号的频谱等价于一种身份ID，给定了频谱，就可以运用逆图傅里叶变换，完整地推导出空域中的图信号。同时，频谱完整地描述了图信号的频域特性，为后面的图信号的采样、滤波、重构等信号处理工作创造了条件。

注意：频域视角是一种全局视角，图信号频谱上的任意一个傅里叶系数，都是对图信号的某种低频或高频特征的定量描述，这种描述即考虑了图信号本身值得大小，也考虑了图的结构信息。