直方图计算介绍

直方图均值化概念

可以参考我的另一篇博文：https://yangyongli.blog.csdn.net/article/details/122663041

直方图计算

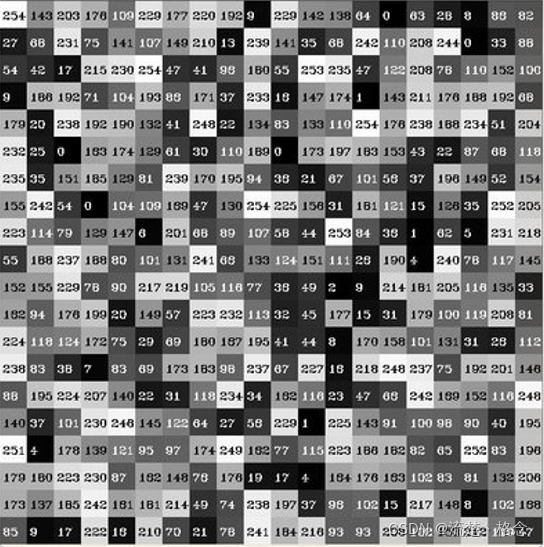
在这里插入图片描述
例如将上面图像像素值建如下直方图：

上述直方图概念是基于图像像素值，其实对图像梯度、每个像素的角度、等一切图像的属性值，我们都可以建立直方图。这个才是直方图的概念真正意义，不过是基于图像像素灰度直方图是最常见的。

直方图最常见的几个属性：

dims 表示维度，对灰度图像来说只有一个通道值dims=1
bins 表示在维度中子区域大小划分，bins=256，划分为256个级别
range 表示值得范围，灰度值范围为[0~255]之间

相关API

split

函数作用：把多通道图像分为多个单通道图像

函数原型：

split(
	const Mat &src, // 输入图像
	Mat* mvbegin	// 输出的通道图像数组
)

minMaxLoc

函数作用：寻找最值函数

函数原型：

void minMaxLoc(
	InputArray src, 
	double* minVal, 
	double* maxVal=0, 
	Point* minLoc=0,
	Point* maxLoc=0,
	InputArray mask=noArray()
)

函数参数：

src ：输入单通道阵列
minVal ：返回最小值的指针，若无需返回，此值置为NULL
maxVal：返回最大值的指针，若无需返回，此值置为NULL
minLoc：返回最小位置的指针（二维情况下），若无需返回，此值置为NULL
maxLoc：返回最大位置的指针（二维情况下），若无需返回，此值置为NULL
mask：用于选择子阵列的可选掩膜

calcHist

函数作用：用来计算图像直方图的

函数原型：

calcHist(
	const Mat* images,	// 输入图像指针
	int images,			// 图像数目
	const int* channels,// 通道数
	InputArray mask,	// 输入mask，可选，不用
	OutputArray hist,	// 输出的直方图数据
	int dims,			// 维数
	const int* histsize,// 直方图级数
	const float* ranges,// 值域范围
	bool uniform,	// true by default
	bool accumulate	// false by defaut
)

代码示例

在这里插入图片描述

#include <iostream>
#include <math.h>
#include <opencv2/opencv.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/highgui/highgui_c.h> 
using namespace std;
using namespace cv;

int main(int argc, char** argv) 
{
	// 图像加载
	Mat src = imread("./test2.jpg");
	if (!src.data) {
		printf("could not load image...\n");
		return -1;
	}
	char INPUT_T[] = "input image";
	char OUTPUT_T[] = "histogram demo";
	namedWindow(INPUT_T, CV_WINDOW_AUTOSIZE);
	namedWindow(OUTPUT_T, CV_WINDOW_AUTOSIZE);
	imshow(INPUT_T, src);

	// 分通道显示
	vector<Mat> bgr_planes;
	split(src, bgr_planes);
	//imshow("single channel demo", bgr_planes[0]);

	// 计算直方图
	int histSize = 256;
	float range[] = { 0, 256 };
	const float *histRanges = { range };
	Mat b_hist, g_hist, r_hist;
	calcHist(&bgr_planes[0], 1, 0, Mat(), b_hist, 1, &histSize, &histRanges, true, false);
	calcHist(&bgr_planes[1], 1, 0, Mat(), g_hist, 1, &histSize, &histRanges, true, false);
	calcHist(&bgr_planes[2], 1, 0, Mat(), r_hist, 1, &histSize, &histRanges, true, false);

	// 归一化
	int hist_h = 400;	// 直方图图像高
	int hist_w = 512;	// 直方图图像宽
	int bin_w = hist_w / histSize;
	Mat histImage(hist_w, hist_h, CV_8UC3, Scalar(0, 0, 0));
	normalize(b_hist, b_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
	normalize(g_hist, g_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
	normalize(r_hist, r_hist, 0, hist_h, NORM_MINMAX, -1, Mat());

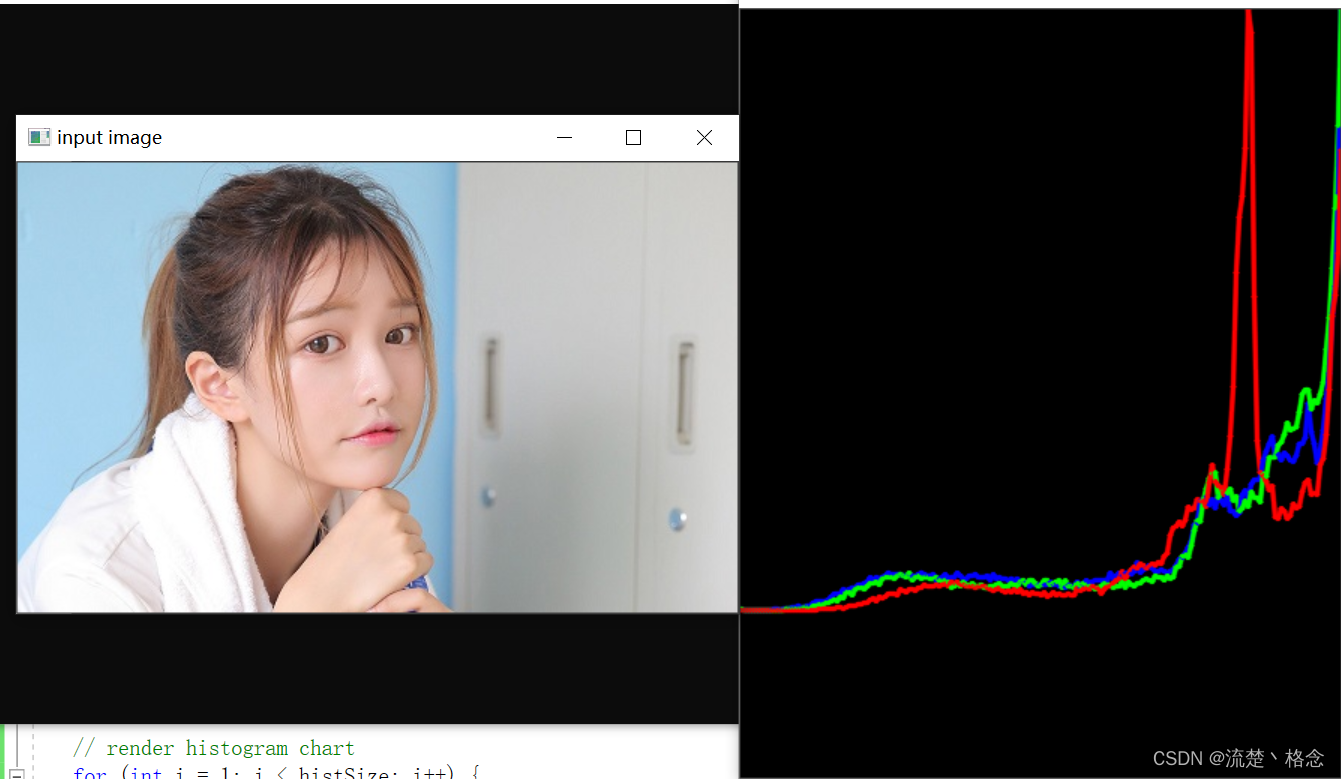
	// render histogram chart
	for (int i = 1; i < histSize; i++) {
		line(histImage, Point((i - 1)*bin_w, hist_h - cvRound(b_hist.at<float>(i - 1))), 
			Point((i)*bin_w, hist_h - cvRound(b_hist.at<float>(i))), Scalar(255, 0, 0), 2, LINE_AA);

		line(histImage, Point((i - 1)*bin_w, hist_h - cvRound(g_hist.at<float>(i - 1))),
			Point((i)*bin_w, hist_h - cvRound(g_hist.at<float>(i))), Scalar(0, 255, 0), 2, LINE_AA);

		line(histImage, Point((i - 1)*bin_w, hist_h - cvRound(r_hist.at<float>(i - 1))),
			Point((i)*bin_w, hist_h - cvRound(r_hist.at<float>(i))), Scalar(0, 0, 255), 2, LINE_AA);
	}
	imshow(OUTPUT_T, histImage);

	waitKey(0);
	return 0;
}