[人工智能]Ex5_机器学习_吴恩达课程作业（Python）：偏差预方差（Bias vs Variance）

Ex5_机器学习_吴恩达课程作业（Python）：偏差预方差（Bias vs Variance）

使用说明：

本文章为关于吴恩达老师在Coursera上的机器学习课程的学习笔记。

• 本文第一部分首先介绍课程对应周次的知识回顾以及重点笔记，以及代码实现的库引入。
• 本文第二部分包括代码实现部分中的自定义函数实现细节。
• 本文第三部分即为与课程练习题目相对应的具体代码实现。

0. Pre-condition

This section includes some introductions of libraries.

# Programming exercise 5 for week 6
import numpy as np
import matplotlib.pyplot as plt
import ex5_function as func
from scipy.io import loadmat

00. Self-created Functions

This section includes self-created functions.

• linearRegCost(theta, X, y, l)：损失函数

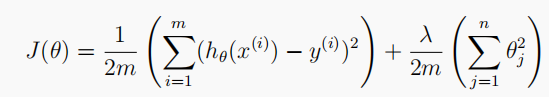
# Cost function of Regularized linear regression  计算损失
# theta: 模型参数； X: 训练特征集; y: 训练标签集; l: 正则化参数lambda
def linearRegCost(theta, X, y, l):
    cost = np.sum((X @ theta - y.flatten()) ** 2)
    reg = (l * (theta[1:] @ theta[1:]))
    return (cost + reg) / (2 * len(X))

• linearRegGradient(theta, X, y, l)：梯度计算函数

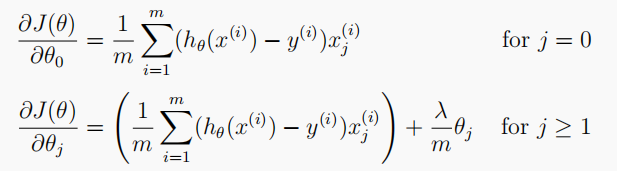
# Gradient of Regularized linear regression  计算梯度
# theta: 模型参数; X: 训练特征集; y: 训练标签集; l: 正则化参数lambda
def linearRegGradient(theta, X, y, l):
    grad = (X @ theta - y.flatten()) @ X
    reg = np.zeros([len(theta)])
    reg[1:] = l * theta[1:]
    reg[0] = 0  # don't regulate the bias term
    return (grad + reg) / len(X)

• trainLinearReg(X, y, l)：正则化线性回归训练

 # Train linear regression using "scipy" lib  训练拟合
 # X: 训练特征集; y: 训练标签集; l: 正则化参数lambda
 def trainLinearReg(X, y, l):
     theta = np.zeros(X.shape[1])
     res = opt.minimize(fun=linearRegCost,
                        x0=theta,
                        args=(X, y, l),
                        method='TNC',
                        jac=linearRegGradient)
     return res.x

• learningCurve(X, y, Xval, yval, l)：绘制学习曲线

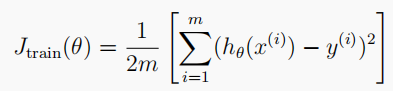
# Plot the learning curves to diagnose bias-variance problem
# 绘制学习曲线，观察训练误差和交叉验证误差随样本数量变化而发生的变化
# X: 训练特征集; y: 训练标签集; Xval: 交叉验证特征集; yval: 交叉验证标签集; l: 正则化参数lambda
def learningCurve(X, y, Xval, yval, l):
    xx = range(1, len(X) + 1)
    train_cost, cv_cost = [], []
    # Gradually expand the size of the set for later computing cost
    for i in xx:
        # Compute temp parameters 计算临时最优参数
        temp_theta = trainLinearReg(X[:i], y[:i], l)
        # Compute on part of the training set 计算此时模型在部分训练集上的损失
        train_cost_i = linearRegCost(temp_theta, X[:i], y[:i], 0)
        # Compute on the whole cross validation set 计算此时模型在整个验证集上的损失
        cv_cost_i = linearRegCost(temp_theta, Xval, yval, 0)
        # Record costs
        train_cost.append(train_cost_i)
        cv_cost.append(cv_cost_i)
    plt.figure(figsize=[10, 6])
    plt.plot(xx, train_cost, label='Training cost')
    plt.plot(xx, cv_cost, label='Cross validation cost')
    plt.xlabel('Number of training examples')
    plt.ylabel('Error')
    plt.title('Learning curves for regularized polynomial regression')
    plt.show()

• `generatePolynomialFeatures(X, power)：多项式特征生成

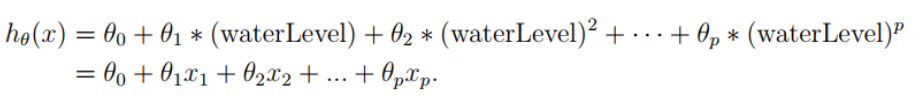
# Generate polynomial features with the given power value
# 根据所给幂值，生成多项式特征
# X: 训练特征集; power: 多项式度数
def generatePolynomialFeatures(X, power):
    Xpoly = X.copy()
    for i in range(2, power + 1):
        Xpoly = np.insert(Xpoly, Xpoly.shape[1],
                          np.power(Xpoly[:, 1], i), axis=1)
    return Xpoly

• computeMeansStds(X)：计算样本均值及标准差，以标准化数据

 # Compute the mean value and standard value of training set to normalize data
 # 计算训练集的样本均值和样本标准差，用以标准化数据
 def computeMeansStds(X):
     means = np.mean(X, axis=0)
     stds = np.std(X, axis=0, ddof=1)  # ddof=1指计算样本标准差
     return means, stds

• normalizeFeatures(X, means, stds)：标准化特征

 # Normalize features
 # 标准化特征
 def normalizeFeatures(X, means, stds):
     X_normalized = X.copy()
     X_normalized[:, 1:] = X_normalized[:, 1:] - means[1:]
     X_normalized[:, 1:] = X_normalized[:, 1:] / stds[1:]
     return X_normalized

1. Regularized linear regression

This section includes details of implementing regularized linear regression (正规化线性回归).

• 调用的相关函数在文章头部"Self-created functions"中详细描述。

我们将从可视化数据集开始，其中包含水位变化的历史记录x，以及从大坝流出的水量y。

这个数据集分为了三个部分：

• Training set：训练集。用于训练模型。
• Cross validation set：交叉验证集。用于选择正则化参数theta。
• Test set：测试集。用于评估性能，模型训练及theta的选择中不被使用。

# 1. Regularized linear regression 正规化线性回归
path_data = "../data/ex5data1.mat"
df = loadmat(path_data)

# training set
X, y = df['X'], df['y']
# cross validation set
Xval, yval = df['Xval'], df['yval']
# test set
Xtest, ytest = df['Xtest'], df['ytest']

# Insert ONES as usual
X = np.insert(X, 0, 1, axis=1)
Xval = np.insert(Xval, 0, 1, axis=1)
Xtest = np.insert(Xtest, 0, 1, axis=1)

1.1 Visualization

# 1.1 Visualization 可视化
# Plot the figure
fig, fig_training = plt.subplots(figsize=[10, 6])
fig_training.scatter(X[:, 1:], y, c='r', marker='x')
fig_training.set_xlabel('Change in water level (x)')
fig_training.set_ylabel('Water flowing out of the dam (y)')
fig_training.set_title('Features vs Fitting curve')

以下为所绘制图像：

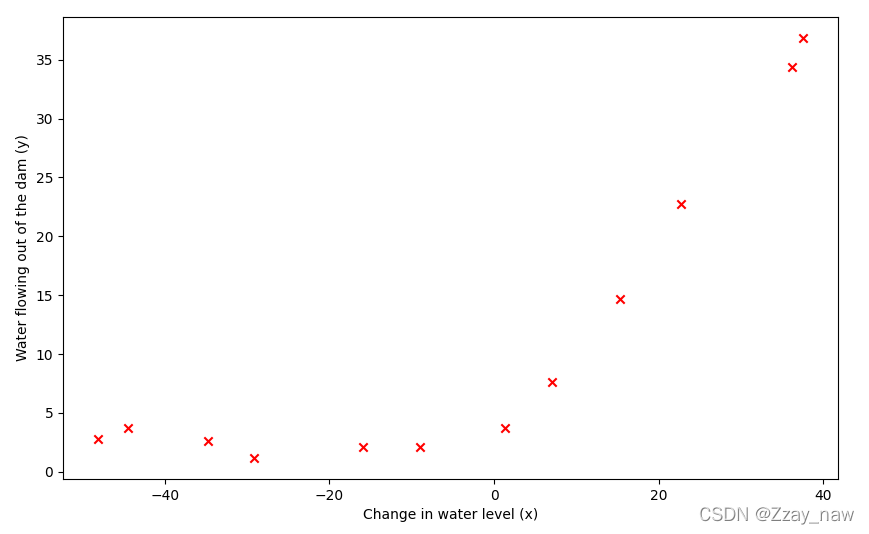
1.2 Cost function

# 1.2 Cost function 计算损失
theta = np.ones(X.shape[1])
res_cost = func.linearRegCost(theta, X, y, l=1)
print(res_cost)

输出结果为：

303.9931922202643

1.3 Gradient

# 1.3 Gradient 计算梯度
res_grad = func.linearRegGradient(theta, X, y, l=1)
print(res_grad)

输出结果为：

[-15.30301567 598.25074417]

1.4 Train and fit

# 1.4 Fit linear regression 拟合优化
fit_theta = func.trainLinearReg(X, y, l=0)
fig_training.plot(X[:, 1], X @ fit_theta)
plt.show()

以下为所绘制图像：

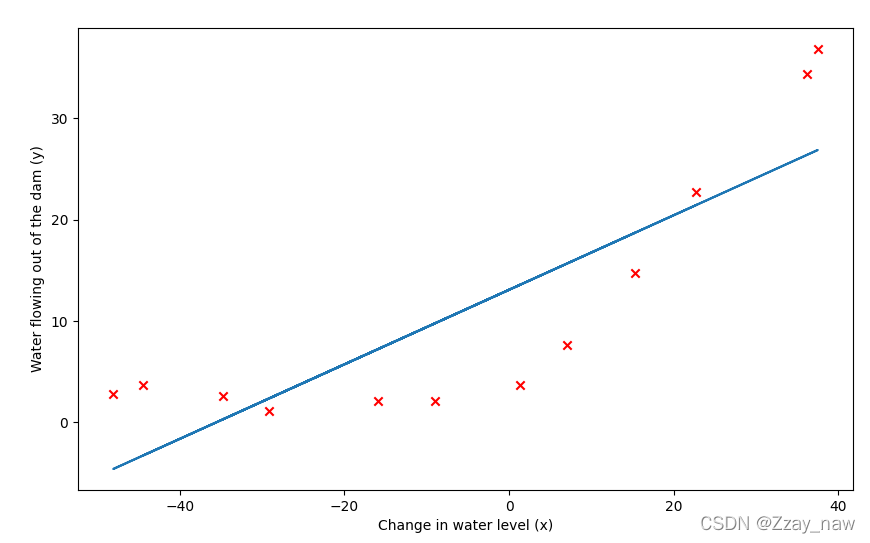
这里我们令$\lambda =0$???，因为此时的线性回归只有两个参数，维度很低，正则化并没有太大用处。并且从图中可以观察分析出，线性模型并不适合拟合此时的数据。

2. Bias vs Variance

This section includes some details of exploring the relationship between “bias” and “variance”.

• 调用的相关函数在文章头部"Self-created functions"中详细描述。

# 2. Bias vs Variance 偏差 vs 方差
path_data = "../data/ex5data1.mat"
df = loadmat(path_data)

# training set
X, y = df['X'], df['y']
# cross validation set
Xval, yval = df['Xval'], df['yval']
# test set
Xtest, ytest = df['Xtest'], df['ytest']

# insert ONES as usual
X = np.insert(X, 0, 1, axis=1)
Xval = np.insert(Xval, 0, 1, axis=1)
Xtest = np.insert(Xtest, 0, 1, axis=1)

2.1 Learning curves

训练样本X从1开始逐渐增加，训练出不同的参数向量θ。接着通过交叉验证样本Xval计算验证误差。

1. 使用训练集的子集来训练模型，得到不同的θ。
2. 通过θ计算训练代价和交叉验证代价，切记此时不要使用正则化，将$\lambda =0$。
3. 计算交叉验证代价时记得整个交叉验证集来计算，无需分为子集。

# 2.1 Learning curves 学习曲线
func.learningCurve(X, y, Xval, yval, 0)

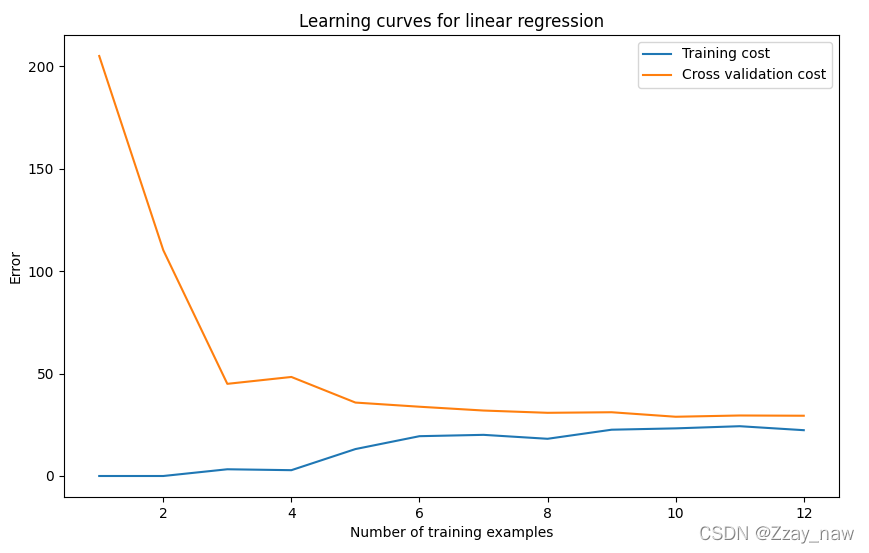
3. Polynomial regression

This section includes some details of exploring polynomial regression.

• 调用的相关函数在文章头部"Self-created functions"中详细描述。

# 3.Polynomial regression 多项式回归
path_data = '../data/ex5data1.mat'
df = loadmat(path_data)

# training set
X, y = df['X'], df['y']
# cross validation set
Xval, yval = df['Xval'], df['yval']
# test set
Xtest, ytest = df['Xtest'], df['ytest']

# insert ONES as usual
X = np.insert(X, 0, 1, axis=1)
Xval = np.insert(Xval, 0, 1, axis=1)
Xtest = np.insert(Xtest, 0, 1, axis=1)

3.1 Learning polynomial regression

此处我们需要对数据进行预处理：

1. X，Xval，Xtest都需要添加多项式特征，这里我们选择增加到6次方，因为若选8次方无法达到作业的效果图，这是因为scipy和octave版本的优化算法不同。
2. 标准化特征。
3. 关于归一化，所有数据集应该都用训练集的均值和样本标准差处理。切记。所以要将训练集的均值和样本标准差存储起来，对后面的数据进行处理。而且注意这里是样本标准差而不是总体标准差，使用np.std()时，将ddof=1则是样本标准差，默认=0是总体标准差。而pandas默认计算样本标准差。

# 3.1 Learning Polynomial regression 多项式回归

power = 6 # Value of power 幂值

# Compute means and stds  计算样本均值和标准差
train_means, train_stds = func.computeMeansStds(
    func.generatePolynomialFeatures(X, power))

# Normalize features for different sets  标准化特征
X_normalized = func.normalizeFeatures(
    func.generatePolynomialFeatures(X, power), train_means, train_stds)
Xval_normalized = func.normalizeFeatures(
    func.generatePolynomialFeatures(Xval, power), train_means, train_stds)
Xtest_normalized = func.normalizeFeatures(
    func.generatePolynomialFeatures(Xtest, power), train_means, train_stds)

# Fit data  训练参数
theta = func.trainLinearReg(X_normalized, y, l=0)
x = np.linspace(-75, 55, 50)
xmat = x.reshape(-1, 1)
xmat = np.insert(xmat, 0, 1, axis=1)

# Generate polynomial features  生成多项式特征
Xmat = func.generatePolynomialFeatures(xmat, power)
Xmat_normalized = func.normalizeFeatures(Xmat, train_means, train_stds)

# Plot the data  可视化
plt.figure(figsize=[10, 6])
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam (y)')
plt.title('Features vs Fitting curve (λ = 0)')
plt.plot(x, Xmat_normalized @ theta, c='b')
plt.scatter(X[:, 1:], y, c='r', marker='x')
plt.show()

# Learning curves  绘制学习曲线
func.learningCurve(X_normalized, y, Xval_normalized, yval, l=0)

• 以下是 $\lambda =0$? 时所绘制的拟合曲线及学习曲线：

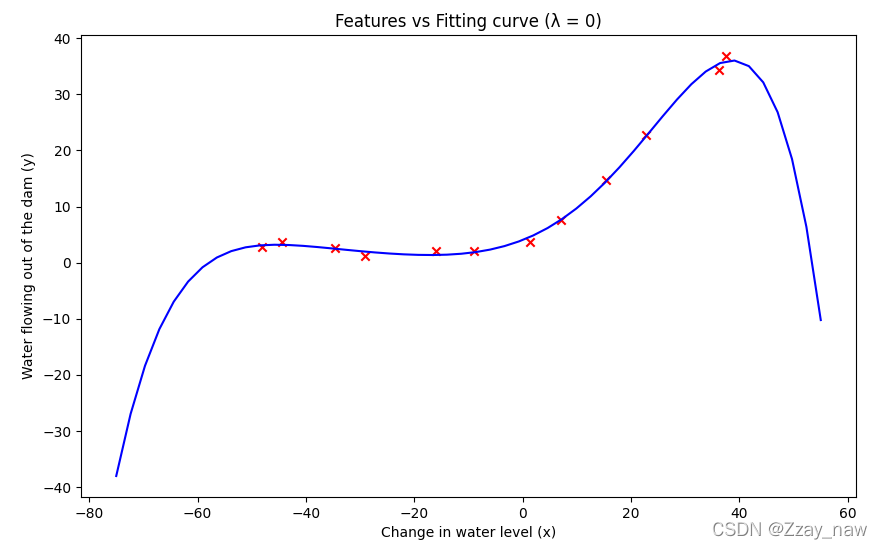
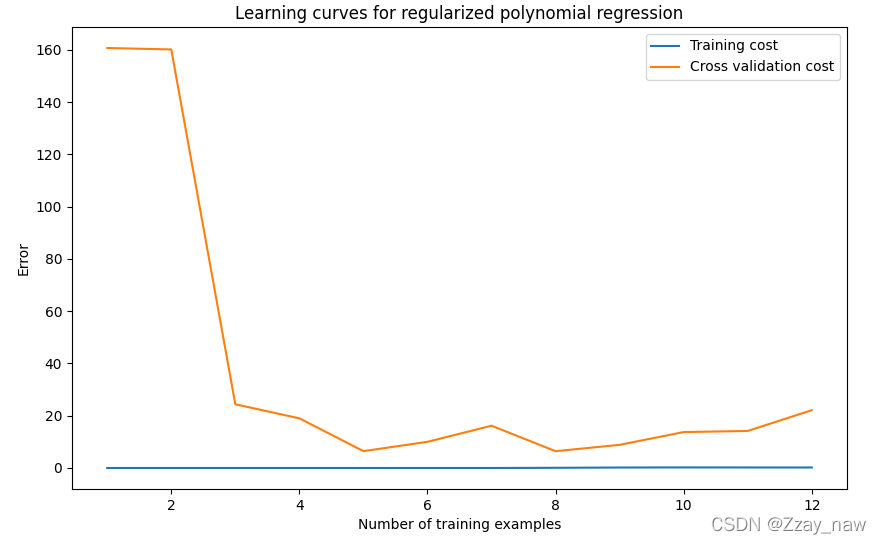
通过观察学习曲线可分析得，此时为**过拟合（overfitting）**状态，即低偏差，高方差（low bias & high variance）。

3.2 Adjust regularization parameter λ

# 3.2 Adjust the regularization parameter

# lambda = 1
theta = func.trainLinearReg(X_normalized, y, l=1)
plt.figure(figsize=[10, 6])
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam (y)')
plt.title('Features vs Fitting curve (λ = 1)')
plt.plot(x, Xmat_normalized @ theta, c='b')
plt.scatter(X[:, 1:], y, c='r', marker='x')
plt.show()
func.learningCurve(X_normalized, y, Xval_normalized, yval, l=1)

# lambda = 1100
theta = func.trainLinearReg(X_normalized, y, l=100)
plt.figure(figsize=[10, 6])
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam (y)')
plt.title('Features vs Fitting curve (λ = 100)')
plt.plot(x, Xmat_normalized @ theta, c='b')
plt.scatter(X[:, 1:], y, c='r', marker='x')
plt.show()
func.learningCurve(X_normalized, y, Xval_normalized, yval, l=100)

• 以下是 $\lambda =1$?? 时所绘制的拟合曲线及学习曲线：

  
  

  通过观察学习曲线可分析得，此时拟合效果良好，即低偏差，低方差（low bias & low variance）。

• 以下是 $\lambda =100$?? 时所绘制的拟合曲线及学习曲线：

  
  

  通过观察学习曲线可分析得，此时是**欠拟合（underfitting）**状态，即高偏差，高方差（high bias & high variance）。

3.3 Select λ using a “cv” set

# 3.3 Select λ using a cross validation set
lambdas = [0., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1., 3., 10.]
train_error, cv_error = [], []

# Compute train errors respectively on those lambda values
for l in lambdas:
    temp_theta = func.trainLinearReg(X_normalized, y, l)
    train_error.append(func.linearRegCost(temp_theta, X_normalized, y, l=0))
    cv_error.append(func.linearRegCost(temp_theta, Xval_normalized, yval, l=0))
    
# Plot the figure
plt.figure(figsize=[10, 6])
plt.plot(lambdas, train_error, label='Training error')
plt.plot(lambdas, cv_error, label='Cross validation error')
plt.legend(loc=1)
plt.xlabel('Value of λ')
plt.ylabel('Error')
plt.title('λ vs Error')
plt.show()

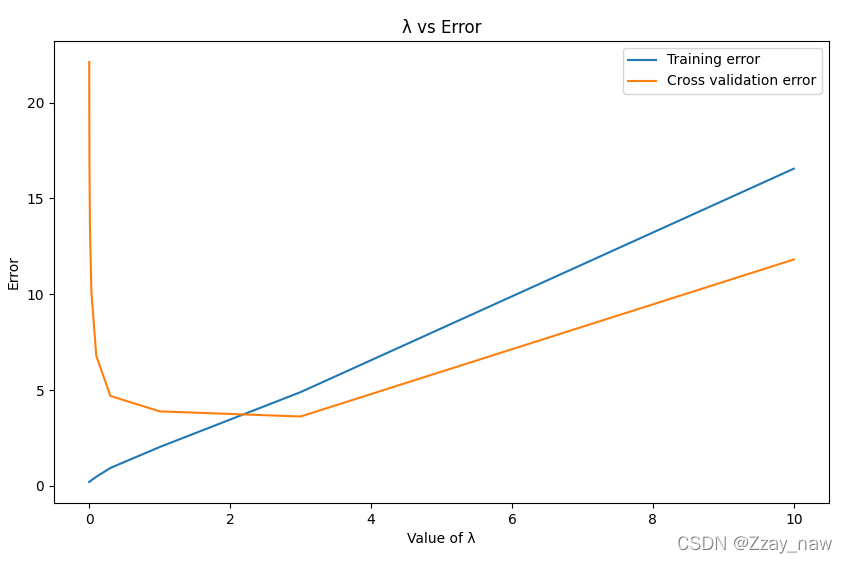
可以观察得出，此时使得cross validation error最小的参数λ值为3。

3.4 Compute test error

# 3.4 Compute test error
lambdas = [0., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1., 3., 10.]
test_error = []
# Compute test errors respectively on those lambda values
for l in lambdas:
    temp_theta = func.trainLinearReg(X_normalized, y, l)
    test_error.append(func.linearRegCost(temp_theta, Xtest_normalized, ytest, l))
# Plot the figure
plt.figure(figsize=[10, 6])
plt.plot(lambdas, test_error, label='Test error')
plt.legend(loc=1)
plt.xlabel('Value of λ')
plt.ylabel('Test error')
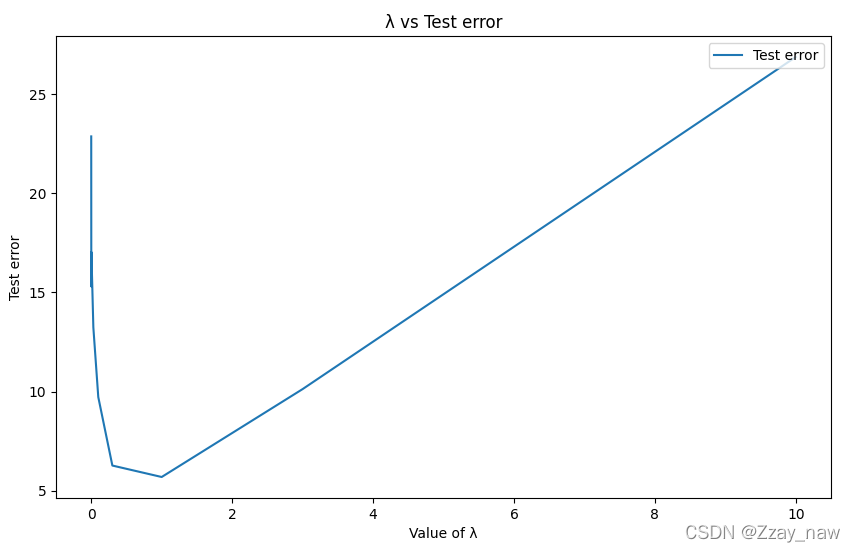
plt.title('λ vs Test error')
plt.show()

以下为所绘制图像：