[人工智能] Python - MindSpore CPU简单线性函数拟合、二次函数曲线拟合

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> Python - MindSpore CPU简单线性函数拟合、二次函数曲线拟合 -> 正文阅读

[人工智能]Python - MindSpore CPU简单线性函数拟合、二次函数曲线拟合

通过MindSpore进行线性回归AI训练

Demo1: 对50个离散点进行简单线性函数拟合

from mindspore import context  
context.set_context(mode=context.GRAPH_MODE, device_target="CPU")  #设置为CPU模式
import numpy as np
import matplotlib.pyplot as plt
from mindspore import dataset as ds
from mindspore.common.initializer import Normal
from mindspore import nn
from mindspore import Tensor
from mindspore import Model
import time
from IPython import display
from mindspore.train.callback import Callback


#定义数据集生成函数
def get_data(num, w=3.0, b=4.0):  
    for _ in range(num):
        x = np.random.uniform(-10.0, 10.0)
        noise = np.random.normal(0, 1)  #定义随机噪声干扰，浮动范围0~1
        y = x * w + b + noise  #y=3x+4+noise
        yield np.array([x]).astype(np.float32), np.array([y]).astype(np.float32)

#使用get_data生成50组测试数据，并可视化        
eval_data = list(get_data(50))
x_target_label = np.array([-10, 10, 0.1])
y_target_label = x_target_label * 3 + 4
x_eval_label, y_eval_label = zip(*eval_data)

#绘图
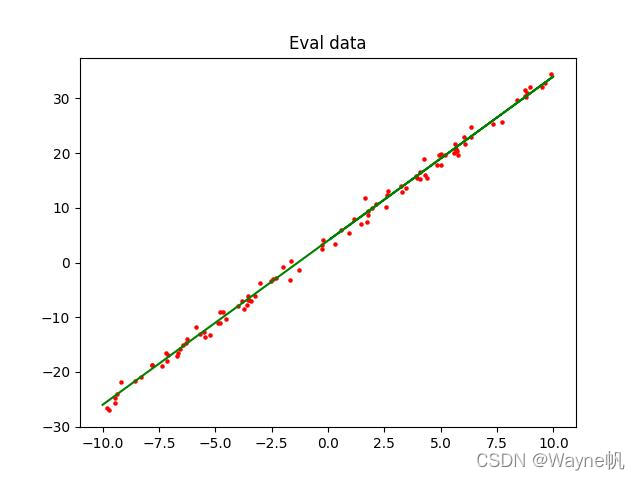
plt.scatter(x_eval_label, y_eval_label, color="red", s=5)
plt.plot(x_target_label, y_target_label, color="green")
plt.title("Eval data")
plt.show()

#数据增强
def create_dataset(num_data, batch_size=16, repeat_size=1):
    input_data = ds.GeneratorDataset(list(get_data(num_data)), column_names=['data', 'label'])  #将生成的数据转换为MindSpore的数据集
    input_data = input_data.batch(batch_size)
    input_data = input_data.repeat(repeat_size)
    return input_data

#通过定义的create_dataset将生成的1600个数据增强为了100组shape为16x1的数据集
data_number = 1600  
batch_number = 16
repeat_number = 1
#使用数据集增强函数生成训练数据，并查看训练数据的格式。
ds_train = create_dataset(data_number, batch_size=batch_number, repeat_size=repeat_number)  #训练数据集
print("The dataset size of ds_train:", ds_train.get_dataset_size())
dict_datasets = next(ds_train.create_dict_iterator())
print(dict_datasets.keys())
print("The x label value shape:", dict_datasets["data"].shape)
print("The y label value shape:", dict_datasets["label"].shape)

class LinearNet(nn.Cell):
    def __init__(self):
        super(LinearNet, self).__init__()
        self.fc = nn.Dense(1, 1, Normal(0.02), Normal(0.02))  #并使用Normal算子随机初始化权重

    def construct(self, x):
        x = self.fc(x)
        return x

net = LinearNet()
model_params = net.trainable_params()
for param in model_params:
    print(param, param.asnumpy())

x_model_label = np.array([-10, 10, 0.1])
y_model_label = (x_model_label * Tensor(model_params[0]).asnumpy()[0][0] +
                 Tensor(model_params[1]).asnumpy()[0])

plt.axis([-10, 10, -20, 25])
plt.scatter(x_eval_label, y_eval_label, color="red", s=5)
plt.plot(x_model_label, y_model_label, color="blue")
plt.plot(x_target_label, y_target_label, color="green")
plt.show()

#定义前向传播网络
net = LinearNet()
net_loss = nn.loss.MSELoss()

#定义反向传播网络
opt = nn.Momentum(net.trainable_params(), learning_rate=0.005, momentum=0.9)
model = Model(net, net_loss, opt)  #关联前向和反向传播网络

def plot_model_and_datasets(net, eval_data):
    weight = net.trainable_params()[0]
    bias = net.trainable_params()[1]
    x = np.arange(-10, 10, 0.1)
    y = x * Tensor(weight).asnumpy()[0][0] + Tensor(bias).asnumpy()[0]
    x1, y1 = zip(*eval_data)
    x_target = x
    y_target = x_target * 3 + 4

    plt.axis([-11, 11, -20, 25])
    plt.scatter(x1, y1, color="red", s=5)
    plt.plot(x, y, color="blue")
    plt.plot(x_target, y_target, color="green")
    plt.draw()
    plt.pause(0.1)# 间隔的秒数：6s
    plt.close()
    
#定义回调函数
class ImageShowCallback(Callback):
    def __init__(self, net, eval_data):
        self.net = net
        self.eval_data = eval_data

    def step_end(self, run_context):
        plot_model_and_datasets(self.net, self.eval_data)
        display.clear_output(wait=True)

epoch = 1  #训练数据集
imageshow_cb = ImageShowCallback(net, eval_data)
model.train(epoch, ds_train, callbacks=[imageshow_cb], dataset_sink_mode=False)  #数据集下沉模式，CPU计算平台设置为False
plot_model_and_datasets(net, eval_data)
for net_param in net.trainable_params():
    print(net_param, net_param.asnumpy())

Answer1: 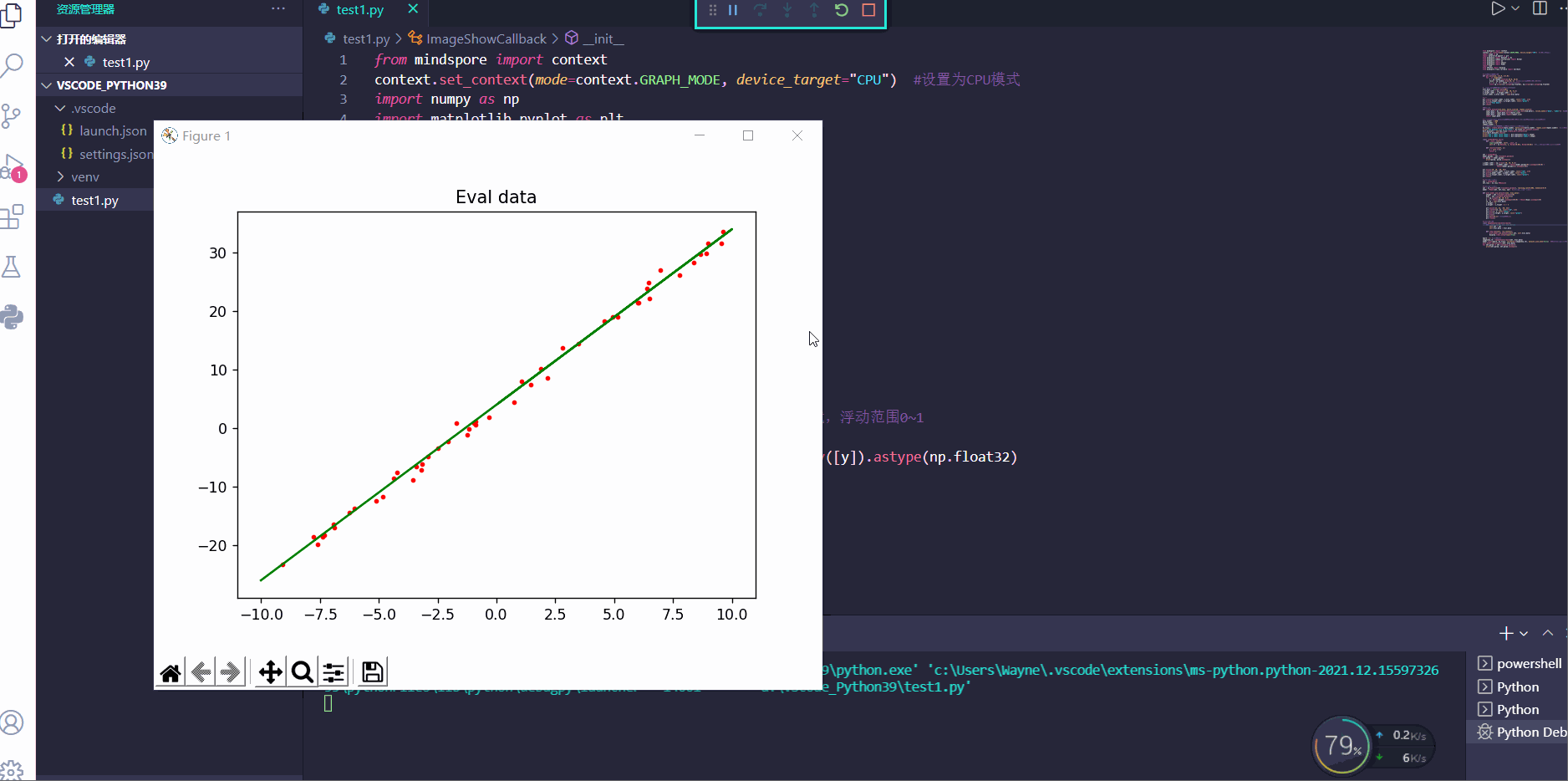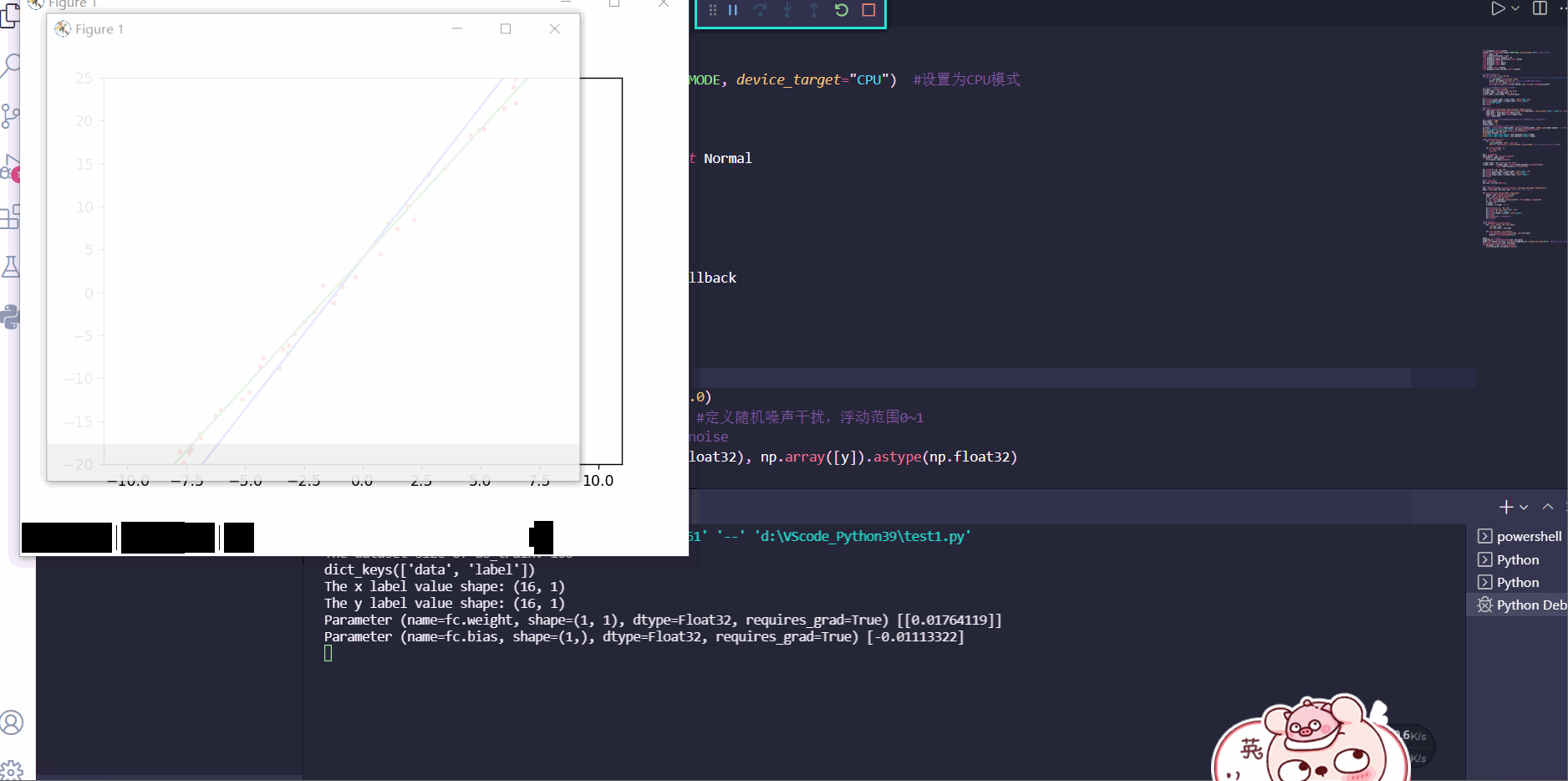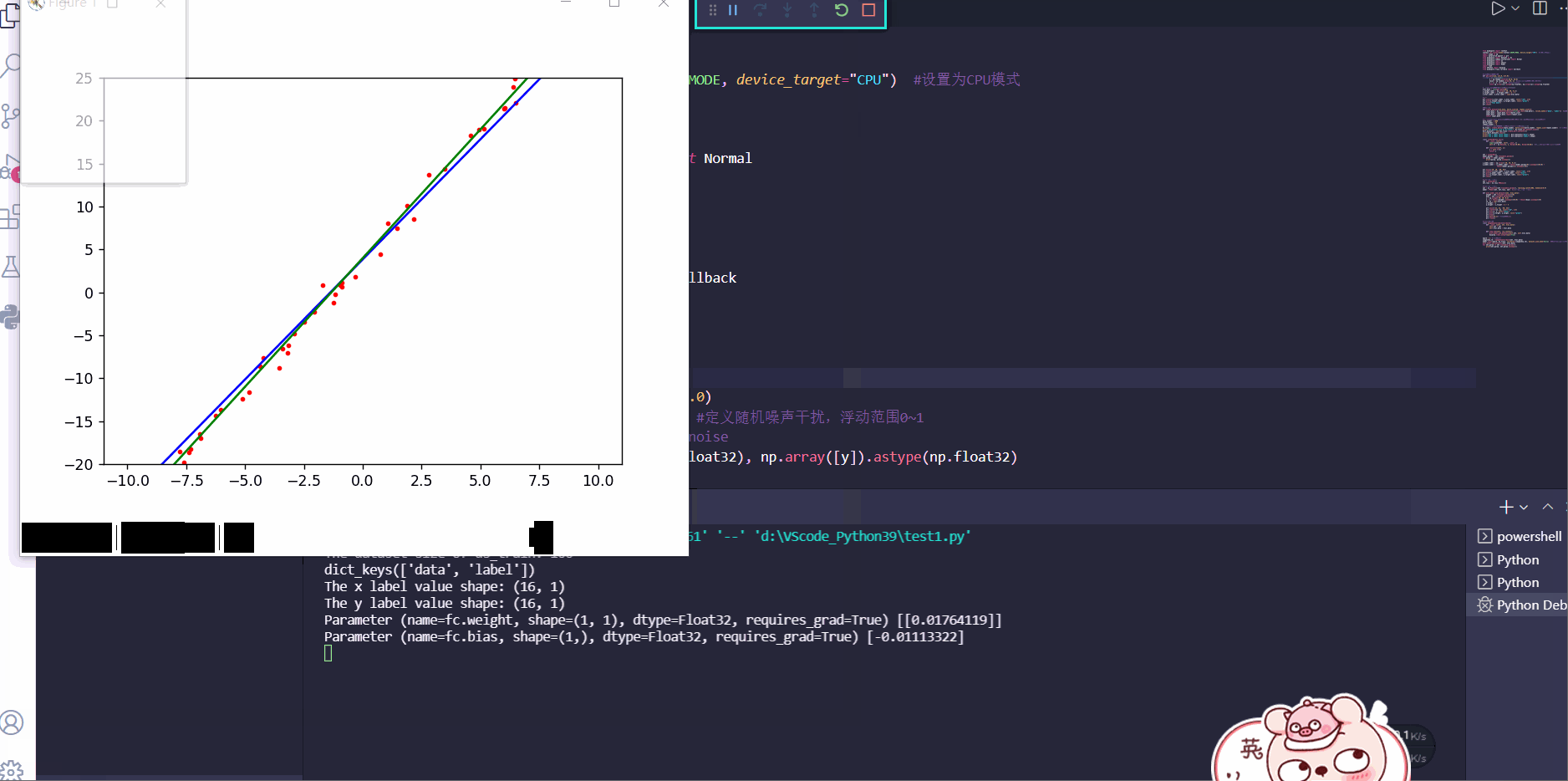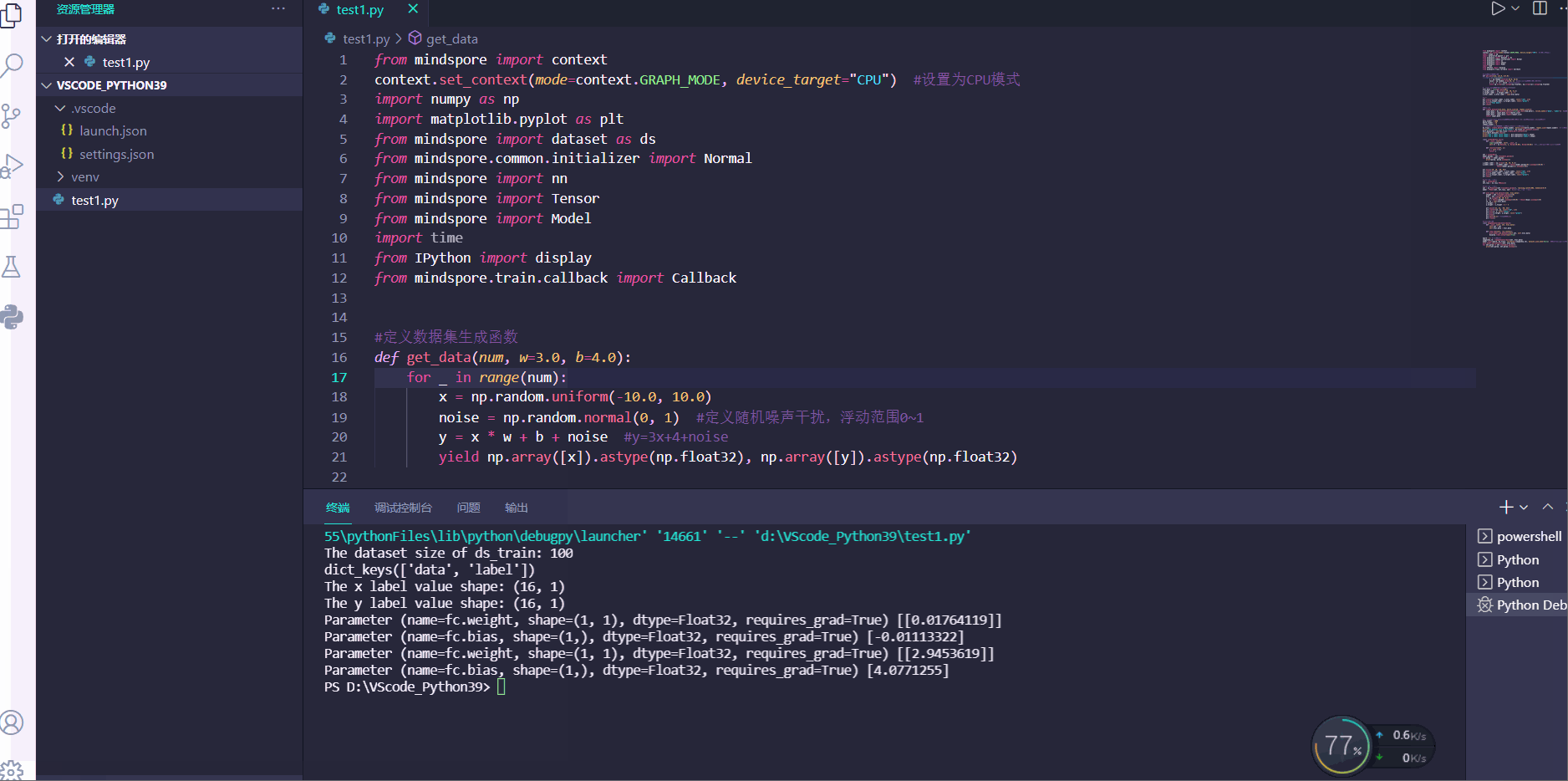在这里插入图片描述
可以看到通过训练，蓝色的线性函数不断逼近绿色的目标函数，
模型初始化参数为：

训练后返回的参数为：

与目标函数 $y = x ? w + b$ 参数 $w = 3, b = 4$ 非常接近。

Demo2: 将训练对象修改为输入100组测试数据，拟合线性函数 $y = 2 ? x + 3$

def get_data(num, w=2.0, b=3.0):  
    for _ in range(num):
        x = np.random.uniform(-10.0, 10.0)

#使用get_data生成100组测试数据，并可视化        
eval_data = list(get_data(100))
x_target_label = np.array([-10, 10, 0.1])
y_target_label = x_target_label * 2 + 3
x_eval_label, y_eval_label = zip(*eval_data)

def plot_model_and_datasets(net, eval_data):
    weight = net.trainable_params()[0]
    bias = net.trainable_params()[1]
    x = np.arange(-10, 10, 0.1)
    y = x * Tensor(weight).asnumpy()[0][0] + Tensor(bias).asnumpy()[0]
    x1, y1 = zip(*eval_data)
    x_target = x
    y_target = x_target * 2 + 3
#相应调成其余相关的参数即可

训练后返回的参数为：
在这里插入图片描述
仍可得到不错的拟合效果。

Demo3: 二次函数曲线拟合

from mindspore import context  
context.set_context(mode=context.GRAPH_MODE, device_target="CPU")  #设置为CPU模式
import numpy as np
import matplotlib.pyplot as plt
from mindspore import dataset as ds
from mindspore.common.initializer import Normal
from mindspore import nn
from mindspore import Tensor
from mindspore import Model
import time
from mindspore.train.callback import LossMonitor


def get_data(num, w=2.0, b=4.0, c=3.0):   #数据生成函数
    for _ in range(num):
        x = np.random.uniform(-1, 1)
        noise = np.random.normal(0, 1)
        y = w * x ** 2 + b * x + c + noise
        # 返回参数的时候压缩在一个数组内
        yield np.array([x**2,x]).astype(np.float32), np.array([y]).astype(np.float32)
 
def get_data2(num, w=2.0, b=4.0, c=3.0):   #生成散点图数据
    for _ in range(num):
        x = np.random.uniform(-10.0, 10.0)
        noise = np.random.normal(0, 1)
        y = w * x ** 2 + b * x + c + noise
        yield np.array([x]).astype(np.float32), np.array([y]).astype(np.float32)
 
 
def create_dataset(num_data, batch_size=16, repeat_size=1):  #数据增强函数
    input_data = ds.GeneratorDataset(list(get_data(num_data)), column_names=['x','y'])
    input_data = input_data.batch(batch_size)
    input_data = input_data.repeat(repeat_size)
    return input_data
 
data_number = 1600
batch_number = 16
repeat_number = 2


ds_train = create_dataset(data_number, batch_size=batch_number, repeat_size=repeat_number)
dict_datasets = next(ds_train.create_dict_iterator())
 
class LinearNet(nn.Cell):
    def __init__(self):
        super(LinearNet, self).__init__()
        # 神经网络的input和output维度设置为2,1
        self.fc = nn.Dense(2, 1, 0.02, 0.02)
 
    def construct(self, x):
        x = self.fc(x)
        return x

eval_data = list(get_data(200))
eval_data2 = list(get_data2(200))
def plot_model_and_datasets(net, eval_data):  #画图函数
    weight = net.trainable_params()[0]
    bias = net.trainable_params()[1]
    x = np.arange(-10, 10, 0.1)
    y = x*x*Tensor(weight).asnumpy()[0][0] +x * Tensor(weight).asnumpy()[0][1]+ Tensor(bias).asnumpy()[0]
    x_eval_label, y_eval_label = zip(*eval_data2)
    x_target = x
    y_target = 2*x_target*x_target +4*x_target+3
    np.linspace(start = 0, stop = 100, num = 5)

    plt.axis([-11, 11, -1, 100])
    plt.scatter(x_eval_label, y_eval_label, color="red", s=5)
    plt.plot(x, y, color="blue")
    plt.plot(x_target, y_target, color="green")
    plt.show()
    time.sleep(0.2)
    
net = LinearNet()
model_params = net.trainable_params()
print ('Param Shape is: {}'.format(len(model_params)))
for net_param in net.trainable_params():
    print(net_param, net_param.asnumpy())
net_loss = nn.loss.MSELoss()
 
optim = nn.Momentum(net.trainable_params(), learning_rate=0.005, momentum=0.9)
model = Model(net, net_loss, optim)

epoch = 1  #训练数据集
model.train(epoch, ds_train, callbacks=[LossMonitor(8)], dataset_sink_mode=False)  #数据集下沉模式，CPU计算平台设置为False

for net_param in net.trainable_params():
    print(net_param, net_param.asnumpy())
    
plot_model_and_datasets(net, eval_data)

Answer3:
目标函数为 $y = 2·x^2+4x+3$ ,

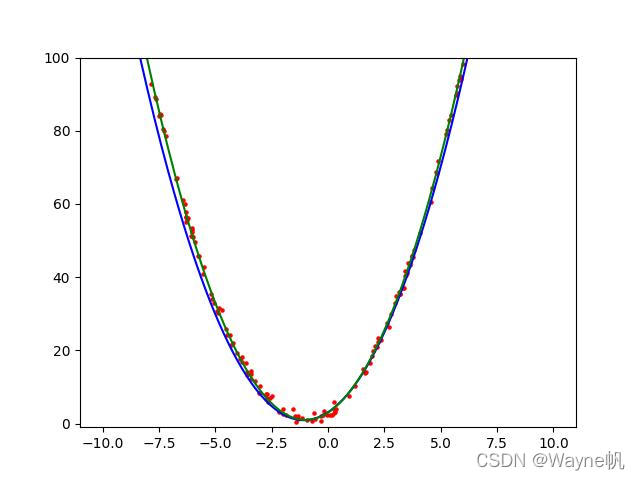
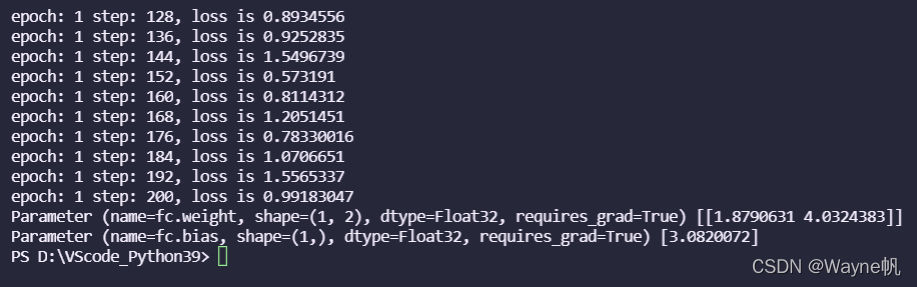
返回参数为：
在这里插入图片描述
Demo4: 对于较小的数据量，另一种简便的方法是利用ployfit多项式拟合，数据量较大的话需要分段进行拟合后再拼接。

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(start = -10, stop = 10, num = 200)
noise = np.random.normal(0, 1)
y = y = 2 * x ** 2 + 4 * x + 3 + noise
z1 = np.polyfit(x, y, 100) # 用3次多项式拟合
p1 = np.poly1d(z1)
print(p1) # 在屏幕上打印拟合多项式
yvals=p1(x) # 也可以使用yvals=np.polyval(z1,x)
plot1=plt.plot(x, y, '*',label='original values')
plot2=plt.plot(x, yvals, 'r',label='polyfit values')
plt.axis([-11, 11, -1, 100])
plt.legend(loc=4) # 指定legend的位置,读者可以自己help它的用法
plt.title('polyfitting')
plt.show()

Answer4:

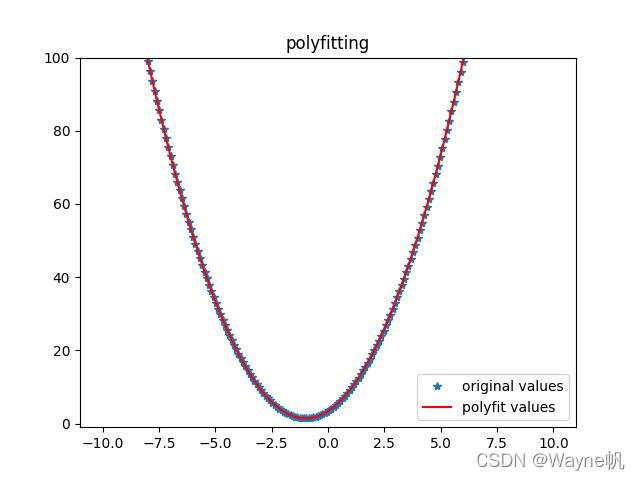
Tips：

调试过程中发现的两个小bug——用MindSpore进行拟合时，x*x*Tensor(weight).asnumpy()[0][0]这种平方项无法用(x**2)*Tensor(weight).asnumpy()[0][0]替代，否则只能拟合从0开始的正半轴部分;
在Demo3拟合的过程中x = np.random.uniform(-1, 1)理论上画出的散点图只有一小段，但改成x = np.random.uniform(-10, 10)后训练返回的参数都是Nan.

参考文档：
简单线性函数拟合
 基于MindSpore实现二次函数的拟合