[人工智能](未完）【机器学习】回归 - 基于广告费预测点击量

一、设置问题

例：广告费和点击量

如果花费200元，点击量大约是500次

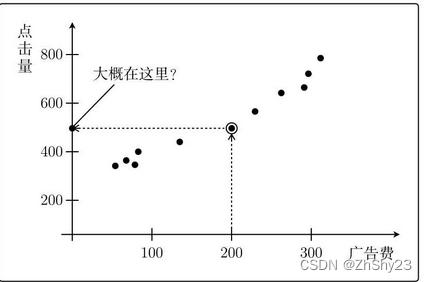
二、定义模型

把图想象为函数。只要知道通过图中各点的函数的形式，就能根据广告费得知点击量。
点击量经常变化，这叫作“点击量中含有噪声”，所以函数并不能完美地通过所有的点。

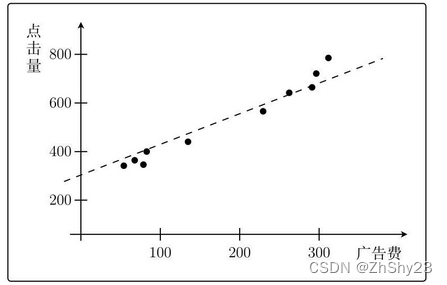
图像为一次函数，确定了斜率和截距，就能确定一次图像的形状。
$$y={\theta }_0+{\theta }_{1}x\text{\hspace{1em}(2.1)}$$

在统计学领域，人们常常使用θ来表示未知数和推测值。采用θ加数字下标的形式，是为了防止当未知数增加时，表达式中大量出现a、b、c、d…这样的符号。这样不但不易理解，还可能会出现符号本身不够用的情况。

如果${\theta }_0=1$，${\theta }_1=2$，表达式$(2.1)$会变成：
$$y=1+2x\text{\hspace{1em}(2.2)}$$

代入$x=1$得出$y=201$
与图像不符，说明${\theta }_0=1$、${\theta }_1=2$是错误的
需要通过算法来得出正确的${\theta }_0,{\theta }_1$

三、最小二乘法

将表达式2.1修改为：
$$f_{\theta }(x)={\theta }_0+{\theta }_{1}x\text{\hspace{1em}(3.1)}$$

将$y$修改为$f_{\theta }(x)$可以看出这是一个含有参数$\theta$，并且和变量$x$相关的函数。如果继续使用$y$，可能会造成后续混乱。

我们拥有的广告费及其相应点击量的数据称为训练数据。
将训练数据中的广告费代入$f_{\theta }(x)$，把得到的点击量与训练数据中的点击量相比较，找出使二者的差最小的$\theta$。

例：选取图上4个点

刚才我们假设了一个$f_{\theta }x=1+2x$的表达式，将表2-1的值代入进行计算

可以看出$y$和$f_{\theta }(x)$完全不同，而我们需要找出${\theta }_0,{\theta }_1$的值使二者最接近。
理想状态下是$y$与$f_{\theta }(x)$之间的误差等于零，我们要做的是让所有点的误差之和尽可能的小。

假设有n个训练数据，那么它们的误差之和可以用表达式（3.2）表示，称为目标函数。（$E(\theta )$的$E$是误差的单词ERROR的首字母）
$$E(\theta )=\frac{1}{2}\sum _{i=1}^n(y^{(i)}?f_{\theta }(x^{(i)}){)}^2\text{\hspace{1em}(3.2)}$$

其中，角标$(i)$表示第$i$个训练数据。
我们对每个训练数据的误差取平方后，全部相加，再乘以$\frac{1}{2}$，以找到使$E(\theta )$的值最小的$\theta$。这样的问题称为最优化问题

使用公式（3.2）来计算表（2-2）中的数据：

$$\begin{array}{rl}E(\theta )& =\frac{1}{2}\sum _{i=1}^n(y^{(i)}?f_{\theta }(x^{(i)}){)}^2\\ & =\frac{1}{2}[(374?117{)}^2+(385?141{)}^2+(375?163{)}^2+(401?169{)}^2]\\ & =112176.5\end{array}\text{\hspace{1em}(3.3)}$$

我们需要不断修改$\theta$的值，使误差越来越小。这种方法叫最小二乘法

最速下降法

使用微分的方法可以求得需要的$\theta$值

例：
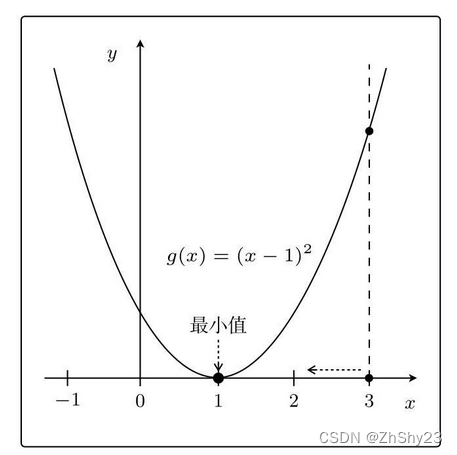
表达式：$g(x)=(x?1{)}^2$的图像：

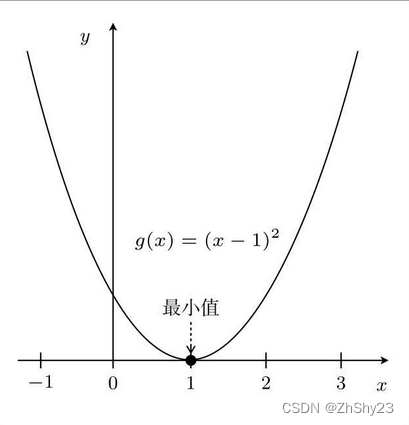
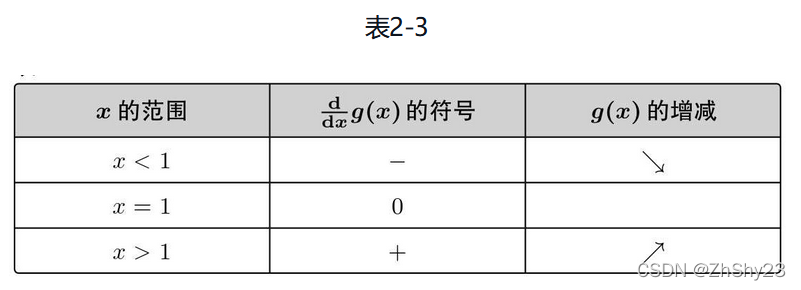
通过微分求出增减表
$$\frac{d}{dx}g(x)=2x?2\text{\hspace{1em}(3.4)}$$

• 比如在$x=3$这一点，为了使$g(x)$的值减小，我们需要向左移动x，也就是必须减小x。
  

• 如果在另一侧$x=?1$，为了使$g(x)$变小，需要向右移动x，也就是增大x
  
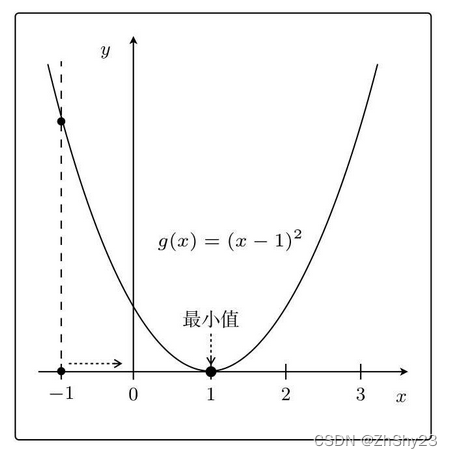
  只要向与导数的符号相反的方向移动x,g(x)就会自然而然地沿着最小值的方向前进。
  最速下降法\梯度下降法：
  $$x:=x?\eta \frac{d}{dx}g(x)\text{\hspace{1em}(3.5)}$$
  (用上一个x来定义新的x)

• $\eta$ - 学习率的正常数。根据学习率的大小，到达最小值的更新次数也会发生变化

代入具体值：

• 从$\eta =1,x=3$开始
  $$\begin{array}{rl}& x:=3?1(2?3?2)=?1\\ & x:=?1?1(2??1?2)=3\\ & x:=3?1(2?3?2)=?1\end{array}\text{\hspace{1em}(3.6)}$$
• 从$\eta =0.1,x=3$开始
  $$\begin{array}{rl}& x:=3?0.1?(2?3?2)=2.6\\ & x:=2.6?0.1?(2?2.6?2)=2.3\\ & x:=2.3?0.1?(2?2.3?2)=2.1\\ & x:=2.1?0.1?(2?2.1?2)=1.9\end{array}\text{\hspace{1em}(3.7)}$$

如果η较大，那么x:=x-η(2x-2)会在两个值上跳来跳去，甚至有可能远离最小值。这就是发散状态。而当η较小时，移动量也变小，更新次数就会增加，但是值确实是会朝着收敛的方向而去。

对于目标函数：$E(\theta )=\frac{1}{2}{\sum }_{i=1}^n(y^{(i)}?f_{\theta }(x^{(i)}){)}^2$，和$g(x)$一样是开口向上的形状，所以刚才的公式也同样适用于它。
不过目标函数中包含$f_{\theta }(x)$，即两个参数${\theta }_0,{\theta }_1$，需要使用偏微分：
$$\begin{array}{rl}& {\theta }_0:={\theta }_0?\eta \frac{?E}{?{\theta }_0}\\ & {\theta }_1:={\theta }_1?\eta \frac{?E}{?{\theta }_1}\end{array}\text{\hspace{1em}(3.9)}$$

省略中间求导步骤
最终得出的公式：
$$\begin{array}{rl}& {\theta }_0:={\theta }_0?\eta \sum _{i=1}^n(f_{\theta }(x^{(i)})?y^{(i)})\\ & {\theta }_1:={\theta }_1?\eta \sum _{i=1}^n(f_{\theta }(x^{(i)})?y^{(i)})x^{(i)}\end{array}\text{\hspace{1em}(3.18)}$$