D-S证据理论
在信息融合技术领域中，信息融合算法是研巧的核也技术。目前的主流的信息融合方法大致可Ｗ分为两大类：概率统计类方法和人工智能方法。
其中概率统计类方法主要流行的数学工具或方法有如下几种：
一是采用最简单直观的数学运算融合的加权平均法。
二是多用于实时融合动态低层次冗余数据的卡尔曼滤波法。
三是把每个传感器进行贝叶斯计算并将各物体的关联概率组成概率分布函数，然后使关联的概率分布函数的似然函数最小，进而得到最终融合算法的多贝叶斯估计法。
四是适用于不确定问题推理的证据理论。
而人工智能则主要包括：利用多值逻辑推理，根据模糊集合理论的何种算法对各命题进行合并计算，最终实现数据融合的模糊攫辑理论；利用神经网络的信号处理能力和自动推理能力实现多传感器数据融合的神经网络法等。
在涉及到数据融合的时候，我们很多人都可能接触到一个名词D-S证据理论，那么这到底是什么意思呢？如果下次看到了这个名词，不要跳过，仔细看看其实很简单。
Dempster-Shafer 证据理论首先由 Dempster 提出，构造了不确定性推理的一般框架，
后来 Shafer 对其进行了扩展和补充，最终形成了证据理论的整体框架。D-S 证据理论在
没有先验信息的情况下可以对不确定性和不精确性进行有效处理，因此它广泛应用于各
种数据融合领域，作为一种不确定推理方法，证据理论的主要特点是：Ｄ－Ｓ证据理论算式简单，且具有较为完善的理论基础，其最大的优势在于满足比贝叶斯概率论更弱的条件，能够合理的区分＂不知道＂和＂不确定＂，这就允许人们对不确定性的问题进行建模分析并产生推理结果。
设Θ表示为对一个判决问题所有可能取值的集合，而且Θ中的事件元素相互独立、
互不相容，称这个集合Θ(论文里都长这样
，但其实都一样，是希腊字母theta的大写形式)为辨识框架。即：
Θ={ A1,A2,A3,……,An}
其中,我们称Ai?(其中i=1,2,3……,n)称为识别框架 Θ 的一个事件或元素。
在识别框架 Θ 中，它的任意子集Ai 都对应着某问题答案的命题，可以形容这个命题为“A 是问题的答案”。
由辨识框架Θ所有事件组成的集合称为Θ的幂集，用
来表示。
接着我们引入幂集的概念，即识别框架 Θ 全部子集的集合，记作 。
举个简单的例子，家里还剩最后一个苹果，父母出去了，家中留有张一，张二，张三，王四，等几个亲生儿子，那么问题就来了，如果苹果被吃了，究竟是谁吃的？那么我们就将{张一}，{张二}，{张三}，{王四}，{张一，张二}，{张一，张三}，{张一，王四}，{张一，张二,张三}……{张一，张二，张三，王四}纳入我们的辨识框架内。框架内的子集总有一个是问题的答案。
设Θ为识别框架，ｍ是从集合2Θ到[0,1]的映射，A表示识别框架Θ的任一子集，记做A?Θ
且满足：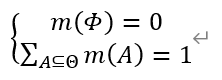
则称m(A)为事件A的基本信任分配函数（BPA）或者mass函数。BPA反映了证据对识别框架中的命题A的支持程度，说是函数其实是个数字值，但是因为是把可能性映射到[0，1]范围内的具有函数的要素。而mΦ=0反映了证据对于空集是不产生任何支持度的。
其实这个基本信任分配函数作用如其名，就是将信任数值化并分配给命题的元素
????????????? 比如有这么一个证据E1：隔壁老王去过张家，认为张一吃苹果可能性为0.5所以m1（{张一}）=0.5，张二，张三都很老实可能是一起吃的概率为0.2，m2({张二，张三})=0.2。王四吃的可能性最小为0.1那么m3（{王四}）=0.1。那么还有0.1的概率也就是m1（Θ）=0.1，这是压根不知道是哪种情况，也就是我们常说的”应该”是这几种情况吧，一个”应该”就说明还会有其他情况。如果没有这0.1那么对于老王来说就是肯定只有这几种情况。这个思考过程就把事件A的分配函数定好了。
而在识别框架Θ下的任一子集若有mA>0，则称A为证据的焦元（focal element）
焦元中所包含的识别框架元素的个数称为该焦元的基。当子集A只含有一个元素时，称
为单元素焦元。若含有１个元素，则称为ｎ元素焦元。
就是如果A为{张二，张三}，那么A是二元焦元，这个事A是由张二，张三他俩干的。
?????? 下面讲一下信任函数
设Θ为识别框架，Bel是从集合2Θ到[0,1]的映射，也就是要把感觉的可能性给数字化。让我们的感觉用0-1内的数字来代替，数字大我们感觉发生的可能性大，数字小，我们感觉发生的可能性就小。A表示识别框架Θ的任一子集，记作A?Θ，且满足：
则我们称Bel（A）为A的信任函数（Belief）。信度函数表达了对每个命题的信度分配
这有同学可能就感到迷糊了，我们还以偷吃苹果那个为例，假如此时邻居王二说了另一种看法E2:m1（{张一}）=0.2，m2（{张二，张三}）=0.2，m3（{王四}）=0.5，m4（Θ）=0.1。
那么Bel{张一}（相信是张一干的事这个命题的信任程度）便可以计算出来，如何计算？那么可不是简单的相加，而是要利用D-S证据理论的组合规则了
笔者提醒：
则称 m 为框架Θ上的基本可信度分配。m(A) 被称为?A 的基本可信数。
基本可信数反映了对 A 本身（而不去管它的任何真子集与前因后果）的信度大小。
命题本质上就是一组证据的集合。
命题表达了我们对待认识的目标对象（识别框架）的一种潜在推测，每一个命题都是识别框架的一个子集，对应一个对现实问题的抽象表征。
基本可信度分配是概率论中完备性的一个泛化推广。基本可信数累加和为1，代表着所有命题共同组合在一起，构成了完整的识别框架。
需要注意的是，和随机事件一样，命题本身是一个集合的概念（离散情况下），所以命题可以有子命题，对命题的可信度分配，同样也有子集的概念。
可以看到，信度函数是一系列可信度分配的累计合成结果，这和概率论中随机变量是单个离散随机事件（离散概率）的累计的概念是一致的。
Dempster-Shafer证据合成规则是一种处理多个证据的联合法则，简称Ｄ－Ｓ证据合成规则。在一个给定的识别框架下，我们可以基于不同的证据获得对应的信任函数。此时我们需要一个方法来融合这些结果。假设这些证据不是完全相悖，那么就可以利用Ｄ－Ｓ证据合成规则加计算得到一个新的信任函数。这一新的信任函数称为原来多个信任函数的正交和
设Θ为识别框架，mi是在这一识别框架下的某一证据的BPA，Aj表示证据的焦元，记作Aj?Θ，D-S证据合成规则表示为：
其中，K表示证据间的冲突程度，K值越大，表明证据间的冲突程度越大。而系数1/1-K称为归一化因子。其实真的只看公式的话，比较难理解到底怎么合成证据，为了让大家更好更快的理解这个公式，下面以两个证据合成情况为例，通过空间图示的方式加以介绍。设Θ为识别框架，m1和m2分别是这一识别框架下的两个证据的BPA，用Ai, bj分别表示两个证据的焦元。下面两张图中，分别用线段[0,1]中用某一段长度表示信任分配函数m1(Ai)和m2Bj的值。而总的线段长度为1表示所有命题的BPA的和为1。
|
Figure 1证据m2的基本概率分配值图 |
 |
Figure 2证据m1的基本概率分配图
Figure 3? D-S证据合成公式效果图
在图3中将图2和图1结合起来，可以算出证据合成后的结果。整个大的矩形可以看成总的基本任务分配。其中，竖轴表示m1分配到其对应焦元Ai上的基本信任分配值。而横轴表示m2分配到对应焦元Bj上的基本信任分配值。图中阴影部分表示同时分配到Ai，Bj上的基本信任分配值，用m1(Ai)* m2(Bj)表示。当Ai∩Bj=A时，m1和m2的联合作用就是将m1(Ai)* m2(Bj)确切分配到A上，同时为了使Ai∩Bj=?时分配到空集上的信任分配值为0，需要把
这一部分值丢弃。当丢弃这部分值后，总的信任值会小于1，因此需要在每个信任分配上乘于系数11-K，总而使总信任值为1。
对于多个证据也可采用相同的做法，将基本信任分配函数合成一个。
还记得偷苹果的例子吗，如果现在父母对于谁会吃苹果有自己的感觉判断，父母认为E3：
m1（{张一}）=0.2，m2（{张二，张三}）=0.2，m3（{王四}）=0.3，m4（Θ）=0.3。我们要知道每一个不确定的可能都包含所有的可能也就是为何我们用m4（Θ）来表示不确定的概率。
那么我们就可以整理出：
E1：m1（{张一}）=0.5，m2({张二，张三})=0.2，m3（{王四}）=0.2，m1（Θ）=0.1。
E2: m1（{张一}）=0.3，m2（{张二，张三}）=0.1，m3（{王四}）=0.5，m4（Θ）=0.1。
E3：m1（{张一}）=0.2，m2（{张二，张三}）=0.2，m3（{王四}）=0.3，m4（Θ）=0.3。
那么下面就是激动人心的时刻了，我们该怎么算出张一偷吃苹果这个命题的整体可信度呢？
m({张一}) =[ m1({张一})+m1( Θ )] * [m2({张一}) + m2( Θ )]*[ m3({张一}) + m3( Θ )] - [m1( Θ ) * m2(Θ) * m3(Θ)]=0.120，
同理m（{张二，张三}）=0.050，m（{王四}）=0.108。而对于m（Θ）我们就要将其舍去
因此k=0.278。
这些概率和就不是1了所以我们将其归一化
那么m({张一})=0.179，m（{张二，张三}）=0.388，m（{王四}）=0.503。（有一定误差，可能和不为1，在实际处理的时候浮点数精度会很高，从而减少此类误差）
在处理的过程中，初始D-S理论其实误差和悖论有很多，比如（1）全冲突惇论，（2）1信任惇论，（3）０信任惇论，（4）证据失效惇论，（5）信任偏移惇论，（6）焦元基模糊停论。对于这方面的改进分为三个方面，一是基于对证据源的修正的方法；二是基于对合成规则的修正的方法；三是同时对证据源及合成规则修正的方法。
第一种基于对证据源的修正方案普遍认为,Dempster-shafer证据合成规则本身是没有错误的。造成合成结果惇论的原因往往是因为通过传感器获得的证据受到了外部环境的干扰或某一传感器在检测过程中失效。基于此分析当证据源存在冲突时，只要对证据源进行预处理，淡化干扰因素，得到修正后的证据源，再使用Dempster-shafer合成规则完成合成即可
具体细节在此就不一一详述了，有兴趣的同学可以查阅资料。唉，word还不能直接复制，公式都是自己一点点扣的，排版都乱完了，可惜了。日后我研究到后会更新优化方案，关注我，我们一起学习数据融合。