? ? ? 在深度学习中,损失函数用来评估模型的预测值与真实值之间的差异程度,是模型对数据拟合程度的反映,拟合的越差,损失函数的值越大;反之,损失函数越小,说明模型的预测值就越接近真实值,模型的准确性也就越好。深度学习的模型训练的目标就是使损失函数的值尽可能小。因此损失函数又被称为目标函数。深度学习的模型训练的过程就是不断地最小化损失函数。选择适合的损失函数不仅影响最终预测的准确性,而且影响训练的效率。
? ? ? 常用的损失函数包括:最小均方差损失函数、L1范数损失函数、L2范数损失函数、交叉熵损失函数等。
? ? ? 1948年,香农提出了信息熵的概念,并且发展为一门独立的学科,即信息论。香农将平均自信息量定义为信息熵,简称为熵。在信息论中,信息熵是为了消除不确定性所需的度量,为了验证概率低的事件,需要大量的信息,此时的信息熵很大;相反,为了验证概率高的事件,则需要少量的信息,此时的信息熵很小。
? ? ? 交叉熵用于度量分布之间的信息差异。交叉熵是信息论中的重要概念,熵是对不确定问题的度量准则,而交叉熵是信息论领域的一种度量,建立在熵的基础上,通常是用来度量两个概率分布之间信息的差异。
? ? ? 最小化交叉熵的过程也就是极大似然估计,深度学习训练的目的,就是最小化交叉熵,使预测的数据分布与真实的数据分布尽量相同。
? ? ? 交叉熵损失函数(Cross-Entropy Loss Function)通常被用来解决深度学习中的分类问题。
? ? ? 对于多分类,每个样本都有一个已知的类标签(class label),概率为1.0,所有其它标签的概率为0.0。模型(model)可以估计样本属于每个类别标签的概率。然后可以使用交叉熵来计算两个概率分布之间的差异。
? ? ? 如果一个分类问题具有三个类别,并且一个样本具有第一类的标签,则概率分布将为[1,0,0];如果一个样本具有第二类的标签,则它概率分布为[0,1,0]。
? ? ? PyTorch中的交叉熵损失函数的计算还包含了Softmax。Softmax能将原网络输出转变为概率形式。
? ? ? Softmax交叉熵损失函数是最常用的分类损失函数。若要将样本分为C个类别,在使用Softmax交叉熵损失时,需要将神经网络的最后一层输出设置为C,得到C个分数后输入Softmax交叉熵损失函数。
? ? ? Softmax交叉损失函数实际上分为两步:求Softmax和求交叉熵损失,其中第一步操作可以得到当前样本属于某类别的概率,然后将这些概率与实际值One-Hot向量求交叉熵,因为实际值是仅在第y个位置为1,其它部分为0,所以最终只保留了第y个位置的交叉熵。
? ? ? 在深度学习样本训练的过程中,采用One-Hot形式进行标签编码,再计算交叉熵损失。在使用交叉熵损失函数的网络训练之前,需要将样本的实际值也转化为概率值形式。为达到这个目的,常用的方法为独热编码即One-Hot编码,又称一位有效编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都有它独立的寄存器位,并且在任意时候,其中只有一位有效。
? ? ?Softmax的介绍参考:https://blog.csdn.net/fengbingchun/article/details/75220591
? ? ? 交叉熵损失函数公式如下:来自于:https://programmathically.com/an-introduction-to-neural-network-loss-functions/
? ? ?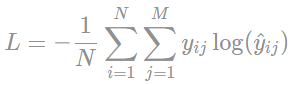
?? ? ? N:样本数;M:类别数;y:预期结果;y hat:模型产生的结果
? ? ? 交叉熵损失函数的C++实现如下:
template<typename _Tp> // y实际值; t预测值; m类别数
_Tp loss_function_cross_entropy(const _Tp* y, const _Tp* t, int m)
{
_Tp loss = 0.;
for (auto i = 0; i < m; ++i)
loss += -y[i] * std::log(t[i]);
return loss;
}? ? ? 测试代码如下:
int test_loss_function()
{
{ // only one sample
const int classes_number = 5;
std::vector<float> sample = { 0.0418, 0.0801, -1.3888, -1.9604, 1.0712 };
std::vector<float> target = { 0, 0, 1, 0, 0 }; // One-Hot
std::vector<float> input(classes_number);
assert(sample.size() == classes_number && target.size() == classes_number && input.size() == classes_number);
fbc::activation_function_softmax(sample.data(), input.data(), classes_number);
float output = fbc::loss_function_cross_entropy(target.data(), input.data(), classes_number);
fprintf(stdout, "output: %.4f\n", output);
}
{ // five samples
const int classes_number = 5, samples_number = 5;
std::vector<std::vector<float>> samples = {{0.0418, 0.0801, -1.3888, -1.9604, 1.0712 },
{0.3519, -0.6115, -0.0325, 0.4484, -0.1736},
{0.1530, 0.0670, -0.3894, -1.0830, -0.4757},
{-1.3519, 0.2115, 1.2325, -1.4484, 0.9736},
{1.1230, -0.5670, 1.0894, 1.9890, 0.03567}};
std::vector<std::vector<float>> targets = {{0, 0, 0, 0, 1},
{0, 0, 0, 1, 0},
{0, 0, 1, 0, 0},
{0, 1, 0, 0, 0},
{1, 0, 0, 0, 0}};
std::vector<std::vector<float>> inputs(samples_number);
assert(samples[0].size() == classes_number && targets[0].size() == classes_number && inputs.size() == samples_number);
float output = 0.;
for (int i = 0; i < samples_number; ++i) {
inputs[i].resize(classes_number);
fbc::activation_function_softmax(samples[i].data(), inputs[i].data(), classes_number);
output += fbc::loss_function_cross_entropy(targets[i].data(), inputs[i].data(), classes_number);
}
output /= samples_number;
fprintf(stdout, "output: %.4f\n", output);
}
return 0;
}? ? ? 执行结果如下:

?? ? ? 调用PyTorch接口测试代码如下:
import torch
import torch.nn as nn
loss = nn.CrossEntropyLoss()
input = torch.tensor([[0.0418, 0.0801, -1.3888, -1.9604, 1.0712]])
target = torch.tensor([2]).long() # target为2,one-hot表示为[0,0,1,0,0]
output = loss(input, target)
print("output:", output)
data1 = [[ 0.0418, 0.0801, -1.3888, -1.9604, 1.0712],
[ 0.3519, -0.6115, -0.0325, 0.4484, -0.1736],
[ 0.1530, 0.0670, -0.3894, -1.0830, -0.4757],
[ -1.3519, 0.2115, 1.2325, -1.4484, 0.9736],
[ 1.1230, -0.5670, 1.0894, 1.9890, 0.03567]]
data2 = [4, 3, 2, 1, 0]
input = torch.tensor(data1)
target = torch.tensor(data2)
output = loss(input, target)
print("output:", output)??? ? ? 执行结果如下:可见C++实现的代码与调用PyTorch接口两边产生的结果完全一致

??? ? ? ?GitHub:
??? ? ? ??? ? ? https://github.com/fengbingchun/NN_Test
??? ? ? ??? ? ? https://github.com/fengbingchun/PyTorch_Test