最近在看七月在线学习课程,学到SVM解读,记录下学习心得和体会,供有需者共勉。
正文:
- 概念定义
支持向量机,它是一种二分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
通俗讲,就是找到空间上能划分训练数据集,并且几何间隔最大的分离超平面。
- 线性分类器概念
给定一个数据集,假设它们分别属于两个类,现在要找到一个线性分类器,把这些数据分成两类。如果用 x 表示数据点, 用 y 表示类别(假设1或者-1,代表两个不同类),一个线性分类器的学习目标,便是要在 n 维的数据空间中找到一个超平面,方程表达式:
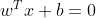 ?
?
?对于线性可分的数据集来说,这样的超平面有无穷多个(即感知机),但是几何间隔最大的分离超平面却是唯一的。

?
- 思路递进
- 哪个超平面对二分类最优?
从直观上而言,这个最优的超平面应该是最适合分开两类数据的直线(假设看成二维)。而判定“最适合”的标准,就是这条直线离直线两边的最近训练集数据都很远(也就是模型的泛化能力最强,不会因验证集稍微超出边界训练集数据,就会作出误判)。所以,得寻找有着最大间隔的超平面,即最中间的那条线,使得距离两边的训练集数据“最宽”。
- 如何判断正负样本?
根据上述公式:w·x + b = 0(W:模型分类函数的法向量),对于任意训练数据x,求x 与W的点乘:
1)当为正样本数据时,根据点乘定义,结果肯定超出截面直线的距离,即X+·W大于某个值,W·Ux ≥?C;
2)当为负样本数据时,数据X- 与法向量的点乘,则小于某个值,W·Ux ≤?C;
此时结论:要找到最优解,就是找到最优W和C(b)的过程。
- 常数值判断,变形为 -1~1判断?
这个 1 和-1 的分类标准来源于logistic回归。Logistic回归目的是从特征学习出一个 0/1 分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷,因此,使用 logistic 函数(或称 sigmoid 函数)将自变量映射到(0,1)上,映射后的值被认为是属于 y=1 的概率。
把 logistic 回归做变形,将使用的结果标签 y = 0 和 y = 1的概率值替换为 y = -1和y = 1的分类值,于是上述得到的分类判断不等式转变为:
W·Ux+ + b ≥?1
W·Ux- + b ≤?-1
即超平面一边的数据点所对应的y全是-1,另一边所对应的y全是1。再变形公式整合为单一形式:
y (W·Ux + b) - 1 ≥ 0,其中y=1或-1 (x为X+时,y=1; x为X-时,y=-1)
- 如何找到最宽距离的超平面
假设X+和X-分别是正负样本在最靠近超平面边界的两个值,要计算超平面的宽度,即计算X+和X-之间距离,用向量相减计算:X+ - X-
进一步等同于求差向量在w法线上的投影距离:(X+ - X-)*(W/|W|)。
再进一步,将X+和X-代入y (W·Ux + b) - 1 =0公式(边界上的测试值,取等号,即最近),得到X+ = 1-b,X- = -1-b,(X+ - X-)*(W/|W|)= 2*(W/|W|)
此时结论:最优超平面求解,只与超平面本身法向量有关,与样本无关。
- 求解极值的方程变形
经过上述步骤,求解最优值(正负样本距离最大化) == 求(2/||W||)最大值 == 求(1/||W||)最大值 == 求||W||最小值 == 求1/2*||W||*||W||最小值(为了后续拉格朗日计算便利的变换)。
至此,求解问题可表示如下:
![]()
- 最终支持向量机公式的得出
因为现在的目标函数是二次的,约束条件是线性的,所以上述求解问题实际是一个凸二次规划问题。
此时,引入了拉格朗日对偶性(Lagrange Duality)的计算。
即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。表达式如下:
![]()
通过求L对W和b的偏导数,当导数为0时,得到最优极值。
此处放上求导过程:
![]()
![]()
将结果代入之前的 L方程:
![]()
此时,得到的拉格朗日函数式已经没有了变量 w,b,只有 α。最终,问题转变为求 α的极值过程。
所谓 Supporting Vector 也在这里显示出来:事实上,所有非 Supporting Vector 所对应的系数都等于零,因此对于新点的内积计算实际上只要针对少量的所谓“支持向量”,而不用顾虑所有的训练数据。