[人工智能]机器学习笔记(第六章支持向量机)

机器学习（周志华著） Datawhale打卡第四天

第六章 支持向量机

基本

• 为什么使用支持向量

对于给定训练集 D = { ( x 1 , y 1 ) , . . . , ( x m , y m ) } , y ∈ { ? 1 , + 1 } D=\{(x_1,y_1),...,(x_m,y_m)\},y\in\{-1,+1\} D={(x1?,y1?),...,(xm?,ym?)},y∈{?1,+1}二分类问题，之前的线性回归的思想是在样本空间找到一个划分超平面，但如下图所示，将样本划分的超平面可能有很多，我们如何得知哪个超平面是最佳的呢。

直观上看，两堆样本的“正中间”的划分超平面，对样本局部扰动的“容忍”性最好。例如，当训练集由于局限性或者噪声的因素而产生一些接近分隔平面的样本点时，其他划分平面会更容易出现错误，而最中间的超平面受影响最小，即“鲁棒”性最好，如何找到这个超平面，就是支持向量机的任务。

• 支持向量

样本空间中，划分超平面用如下方程描述：
w T x + b = 0 其 中 w = { w 1 , w 2 , . . . , w d } 为 法 向 量 , b 为 位 移 项 w^Tx+b=0\\ 其中w=\{w_1,w_2,...,w_d\}为法向量,b为位移项 wTx+b=0其中w={w1?,w2?,...,wd?}为法向量,b为位移项
样本中任意点到超平面的距离$r=\frac{|w^{T}x+b|}{||w||}$,由于这个公式比较重要，下面来证明
$$\begin{gathered} 证：设任意一点为x_0=(x_1^0,x_2^0,...,x_n^0{)}^T \\ 其在超平面上的投影点为x_1=(x_1^1,x_2^1,...,x_n^1{)}^T \\ 有w^T{x}_1+b=0,且有x_1{x}_0与法向量w平行 \\ 因此|w.x_1{x}_0|=||w||.||x_1{x}_0||=||w||.r \\ \begin{array}{rl}w.x_1{x}_0& =w_1(x_1^0?x_1^1)+...w_n(x_n^0?x_n^1)\\ & =w^T{x}_0?w^T{x}_1\\ & =w^T{x}_0+b\end{array} \\ 即r_{x_0}=\frac{|w^T{x}_0+b|}{||w||} \end{gathered}$$

假设超平面$(w,b)$能将样本正确分类，对于二分类的正样本$y_i=+1$,与负样本$y_i=?1$,其应该满足：
$$\{\begin{array}{ll}& w^T{x}_i+b\ge +1,y_i=+1\\ & w^T{x}_i+b\le ?1,y_i=+1\end{array}$$
其中，存在缩放变换$?w?w^{\prime }\text{和}?b?b^{\prime }$，使得距离超平面最近的几个样本点，可使上式等号成立，如图所示，

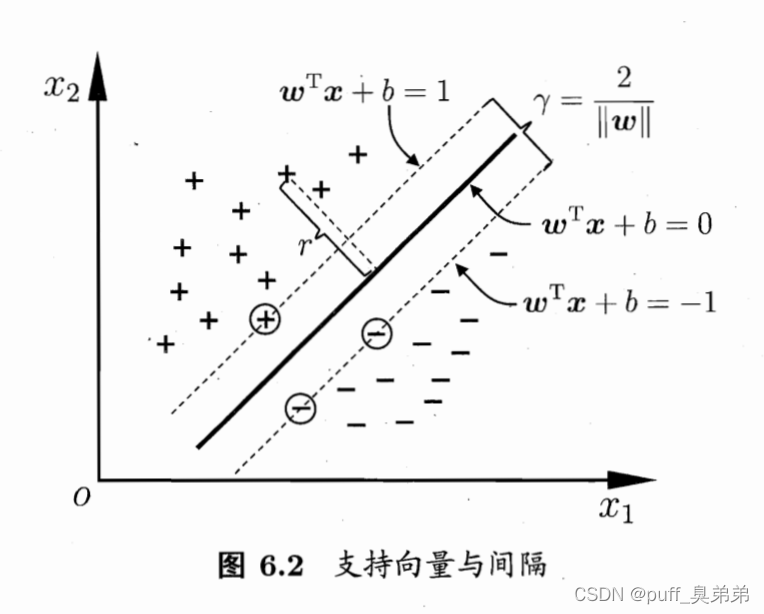
这些使等号成立的向量被称为“支持向量”。

它们到超平面的距离之和为$\gamma =\frac{2}{||w||}$，称为“间隔”。

支持向量的任务便转化为寻找“最大间隔”的划分超平面，即找到合适的$w,b$，使得
$$\begin{gathered} \underset{w,b}{\max }\frac{2}{||w||} \\ s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2...,m \end{gathered}$$
而最大化$||w|{|}^{?1}$等价于最小化$||w|{|}^2$，于是上式可重写为
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||w|{|}^2 \\ s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2...,m \end{gathered}$$
这就是支持向量机(Support Vector Machine,SVM)的基本型。

• 对偶问题

基本型可以直接用现成的优化方法求解，但是求解其对偶问题更为高效。

对基本型使用拉格朗日乘子法可得到其“对偶问题”

$$\begin{gathered} L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1?y_i(w^T{x}_i+b)) \\ 令\frac{?L}{?w}=0,\frac{?L}{?b}=0 \\ 得w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i \\ 0=\sum _{i=1}^m{\alpha }_i{y}_i \end{gathered}$$
代入得对偶问题
$$\begin{gathered} \underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i?\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j \\ s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0, \\ {\alpha }_i\ge 0,i=1,2,...,m \end{gathered}$$
以及KKT条件
$$?\begin{array}{ll}& {\alpha }_i\ge 0\\ & y_{i}f(x_i)?1\ge 0\\ & {\alpha }_i(y_{i}f(x_i)?1)=0\end{array}$$

算法的求解比较复杂，后面再写。。。

• 未完待续。。。