一、特征值和特征向量(只能是方阵)
对于n阶方阵A,如果存在数a和非零n维列向量x,使得Ax=ax,则称a是矩阵A的一个特征值,x是矩阵A属于特征值a的特征向量
#已知n阶方阵A, 求特征值与特征数组
# eigvals: 特征值数组
# eigvecs: 特征向量数组
eigvals, eigvecs = np.linalg.eig(A)
#已知特征值与特征向量,求方阵
S = np.mat(eigvecs) * np.mat(np.diag(eigvals)) * np.mat(eigvecs逆)
案例:
import numpy as np
A = np.mat('3 -2; 1 0')
print(A)
eigvals, eigvecs = np.linalg.eig(A)
print(eigvals)
print(eigvecs)
print(A * eigvecs[:, 0]) # 方阵*特征向量
print(eigvals[0] * eigvecs[:, 0]) #特征值*特征向量
S = np.mat(eigvecs) * np.mat(np.diag(eigvals)) * np.mat(eigvecs.I)
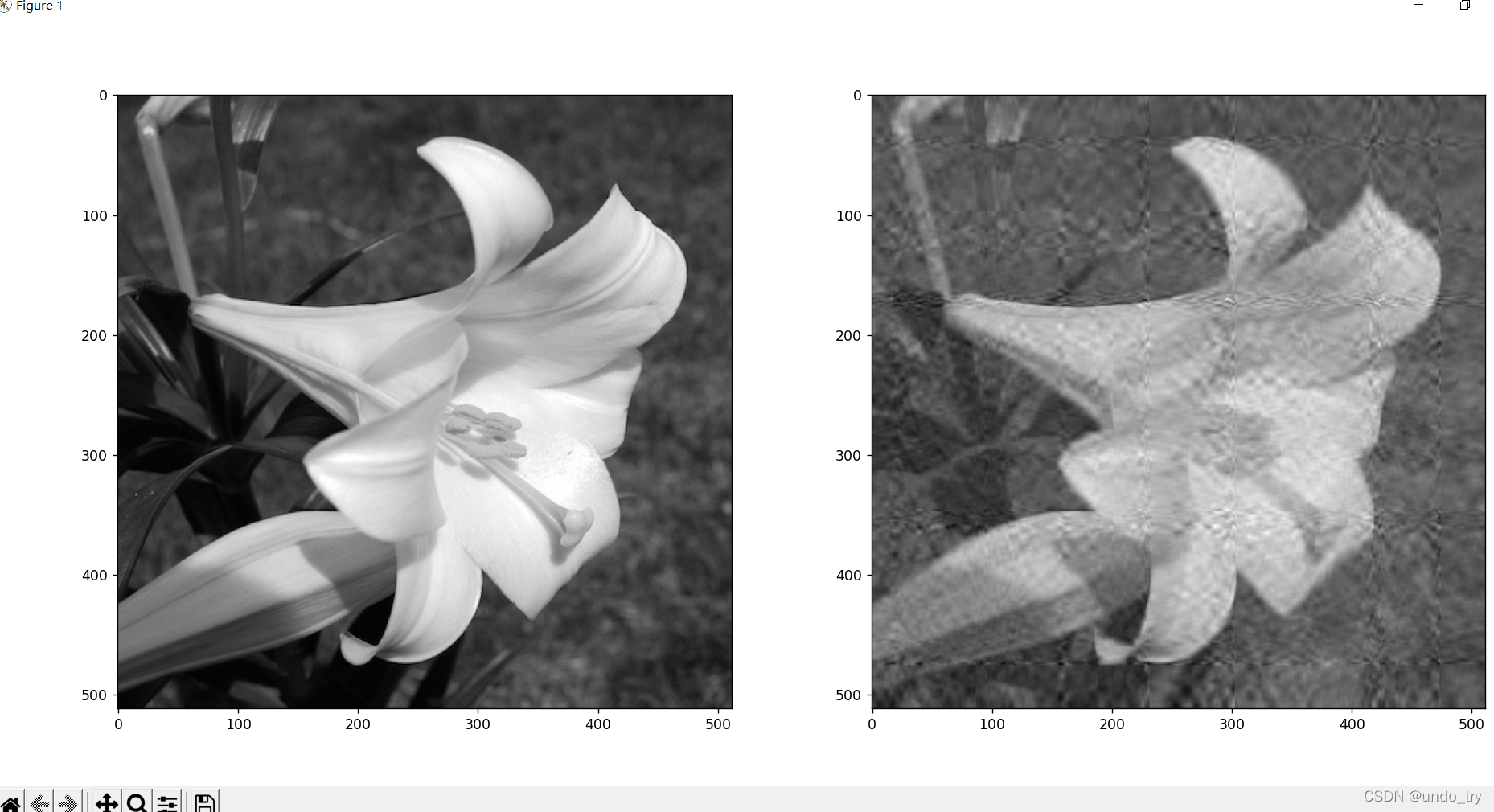
案例:读取图片的亮度矩阵,提取特征值与特征向量,保留部分特征值,重新生成新的亮度矩阵,绘制图片。
"""
特征值和特征向量 提取图片
"""
# import scipy.misc as sm
import imageio
import numpy as np
import matplotlib.pyplot as mp
original = imageio.imread('D:\\python\\...\\lily.jpg',as_gray = True)
print(original.shape)
original = np.mat(original)
# 提取特征值和特征向量
eigvals, eigvecs = np.linalg.eig(original)
print(eigvals,'特征值')
print(eigvecs,'特征向量')
# 抹掉一部分呢特征值 生成新图片
eigvals[50:] = 0
dst = eigvecs * np.diag(eigvals) * eigvecs.I
mp.subplot(121)
mp.imshow(original,cmap='gray') # 灰度映射 越小越偏黑 越大越偏白
mp.xticks()
mp.yticks()
mp.tight_layout()
# 抹掉一部分呢特征值 生成新图片
mp.subplot(122)
mp.imshow(dst.real,cmap='gray') # 灰度映射 越小越偏黑 越大越偏白
mp.xticks()
mp.yticks()
mp.tight_layout()
mp.show()
二、奇异值分解(既可以方阵,又可以非方阵)
有一个矩阵M,可以分解为3个矩阵U、S、V,使得U x S x V等于M。U与V都是正交矩阵(乘以自身的转置矩阵结果为单位矩阵)。那么S矩阵主对角线上的元素称为矩阵M的奇异值,其它元素均为0。
import numpy as np
M = np.mat('4 11 14; 8 7 -2')
print(M)
U, sv, V = np.linalg.svd(M, full_matrices=False)
print(U * U.T)
print(V * V.T)
print(sv)
S = np.diag(sv)
print(S)
print(U * S * V)
案例:读取图片的亮度矩阵,提取奇异值与两个正交矩阵,保留部分奇异值,重新生成新的亮度矩阵,绘制图片。
"""
特征值和特征向量 提取图片
"""
# import scipy.misc as sm
import imageio
import numpy as np
import matplotlib.pyplot as mp
original = imageio.imread('D:\\python\\...\\lily.jpg',as_gray = True)
print(original.shape)
original = np.mat(original)
# 提取特征值和特征向量
eigvals, eigvecs = np.linalg.eig(original)
print(eigvals,'特征值')
print(eigvecs,'特征向量')
# 抹掉一部分呢特征值 生成新图片
eigvals[50:] = 0
dst = eigvecs * np.diag(eigvals) * eigvecs.I
# 奇异值
U , sv, V = np.linalg.svd(original,full_matrices=False)
sv[50:] = 0
dst2 = U * np.diag(sv) * V
mp.subplot(221)
mp.imshow(original,cmap='gray') # 灰度映射 越小越偏黑 越大越偏白
mp.xticks()
mp.yticks()
mp.tight_layout()
# 抹掉一部分呢特征值 生成新图片
mp.subplot(222)
mp.imshow(dst.real,cmap='gray') # 灰度映射 越小越偏黑 越大越偏白
mp.xticks()
mp.yticks()
mp.tight_layout()
# 抹掉一部分呢奇异值 生成新图片
mp.subplot(224)
mp.imshow(dst2.real,cmap='gray') # 灰度映射 越小越偏黑 越大越偏白
mp.xticks()
mp.yticks()
mp.tight_layout()
mp.show()

三、快速傅里叶变换(fft)
什么是傅里叶变换?
法国科学家傅里叶提出傅里叶定理,**任何一条周期曲线,无论多么跳跃或不规则,都能表示成一组光滑正弦曲线叠加之和。**傅里叶变换即是将不规则曲线拆解为一组光滑正弦曲线的过程。
傅里叶变换的目的是可将时域(即时间域)上的信号转变为频域(即频率域)上的信号,随着域的不同,对同一个事物的了解角度也就随之改变,因此在时域中某些不好处理的地方,在频域就可以较为简单的处理。这就可以大量减少处理信号存储量。
例如:弹钢琴
假设有一时间域函数:y = f(x),根据傅里叶的理论它可以被分解为一系列正弦函数的叠加,他们的振幅A,频率ω或初相位φ不同:
y
=
A
1
s
i
n
(
ω
1
x
+
?
1
)
+
A
2
s
i
n
(
ω
2
x
+
?
2
)
+
A
2
s
i
n
(
ω
2
x
+
?
2
)
+
R
y = A_1sin(\omega_1x+\phi_1) + A_2sin(\omega_2x+\phi_2) + A_2sin(\omega_2x+\phi_2) + R
y=A1?sin(ω1?x+?1?)+A2?sin(ω2?x+?2?)+A2?sin(ω2?x+?2?)+R
所以傅里叶变换可以把一个比较复杂的函数转换为多个简单函数的叠加,看问题的角度也从时间域转到了频率域,有些的问题处理起来就会比较简单。
傅里叶变换相关函数
导入快速傅里叶变换所需模块
import numpy.fft as nf
(1) 通过采样数与采样周期求得傅里叶变换分解所得曲线的频率序列
freqs = np.fftfreq(采样数量, 采样周期)
(2) 通过原函数值的序列j经过快速傅里叶变换得到一个复数数组,复数的模代表的是振幅,复数的辐角代表初相位
np.fft(原函数数组) -> 复数数组(表示一组正弦函数)
(3) 通过 复数数组 经过逆向傅里叶变换得到合成的函数值数组
np.ifft(复数数组)->原函数值数组
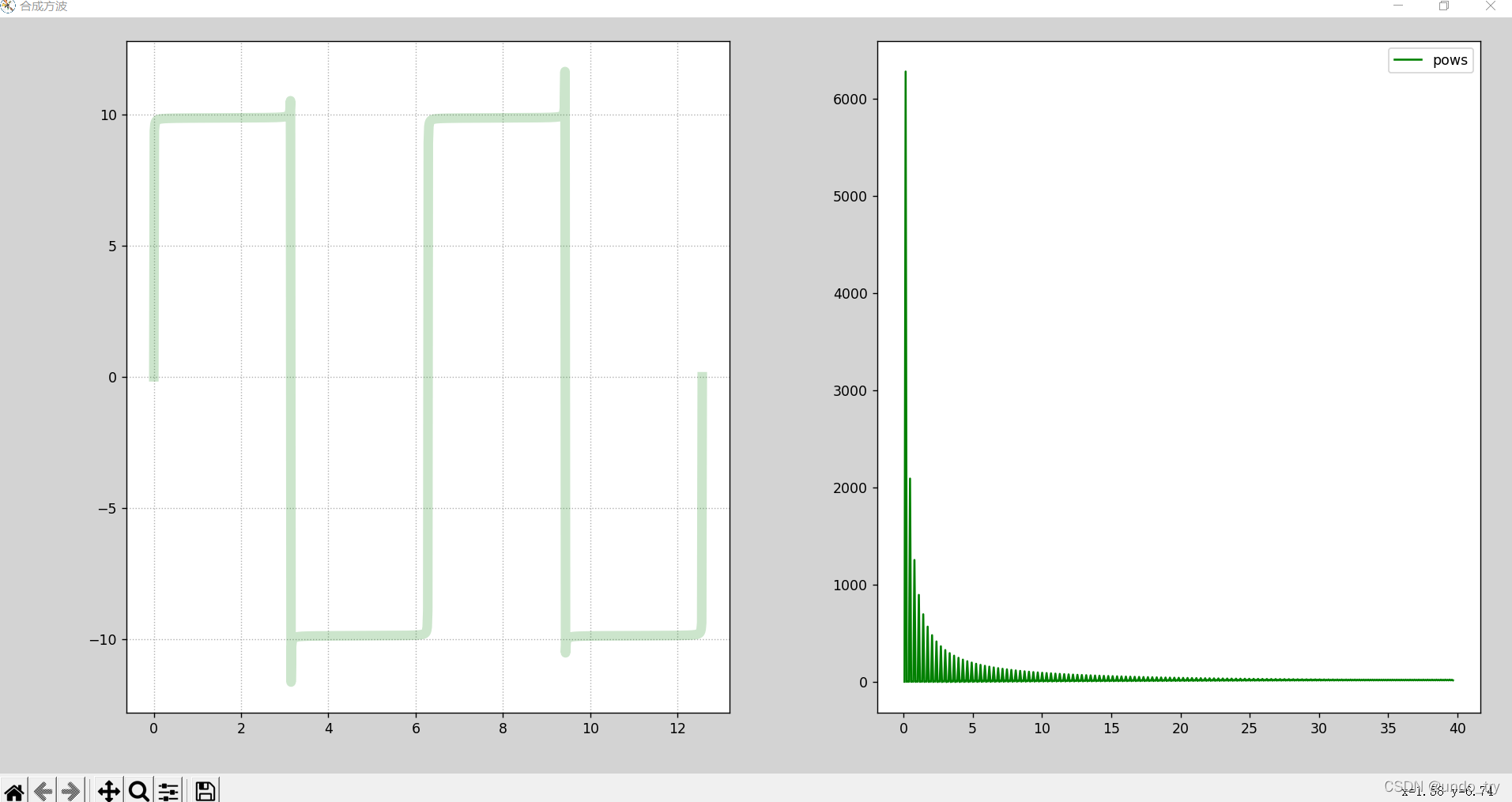
案例:针对方波,绘制时域图与频域图。
import numpy as np
import matplotlib.pyplot as mp
x = np.linspace(0,4 * np.pi,1000)
y = np.zeros(1000)
for i in range(1, 1001, 2):
y += 4 / i * np.pi * np.sin(i * x)
mp.figure('合成方波',facecolor='lightgray')
# 设置该图的题目
mp.title('Chart',fontsize = 18)
# 设置网格线
mp.grid(linestyle=':')
mp.plot(x,y,color = 'purple',label = 'y')
mp.tight_layout()
# 针对合成的方波,做傅里叶变换
import numpy.fft as nf
complex_ary = nf.fft(y)
print(complex_ary.shape,complex_ary.dtype,complex_ary.size)
# 合成波, 逆傅里叶变换
y_ = nf.ifft(complex_ary)
mp.subplot(121)
mp.grid(linestyle=':')
mp.plot(x,y_,color = 'green',label = 'y_',linewidth = 7,alpha = 0.2)
# 绘制频域图像 频率/能量图像
# 通过采样数量和采样周期获取fft的频率数组
freqs = nf.fftfreq(y.size, x[1] - x[0])
pows = np.abs(complex_ary)
print(freqs)
mp.subplot(122)
mp.plot(freqs[freqs > 0],pows[freqs > 0],color = 'green',label = 'pows')
mp.tight_layout()
mp.legend()
mp.show()
基于傅里叶变换的频域滤波
含噪信号是高能信号与低能噪声叠加的信号,可以通过傅里叶变换的频域滤波实现降噪。
通过FFT使含噪信号转换为含噪频谱,去除低能噪声,留下高能频谱后再通过IFFT留下高能信号。
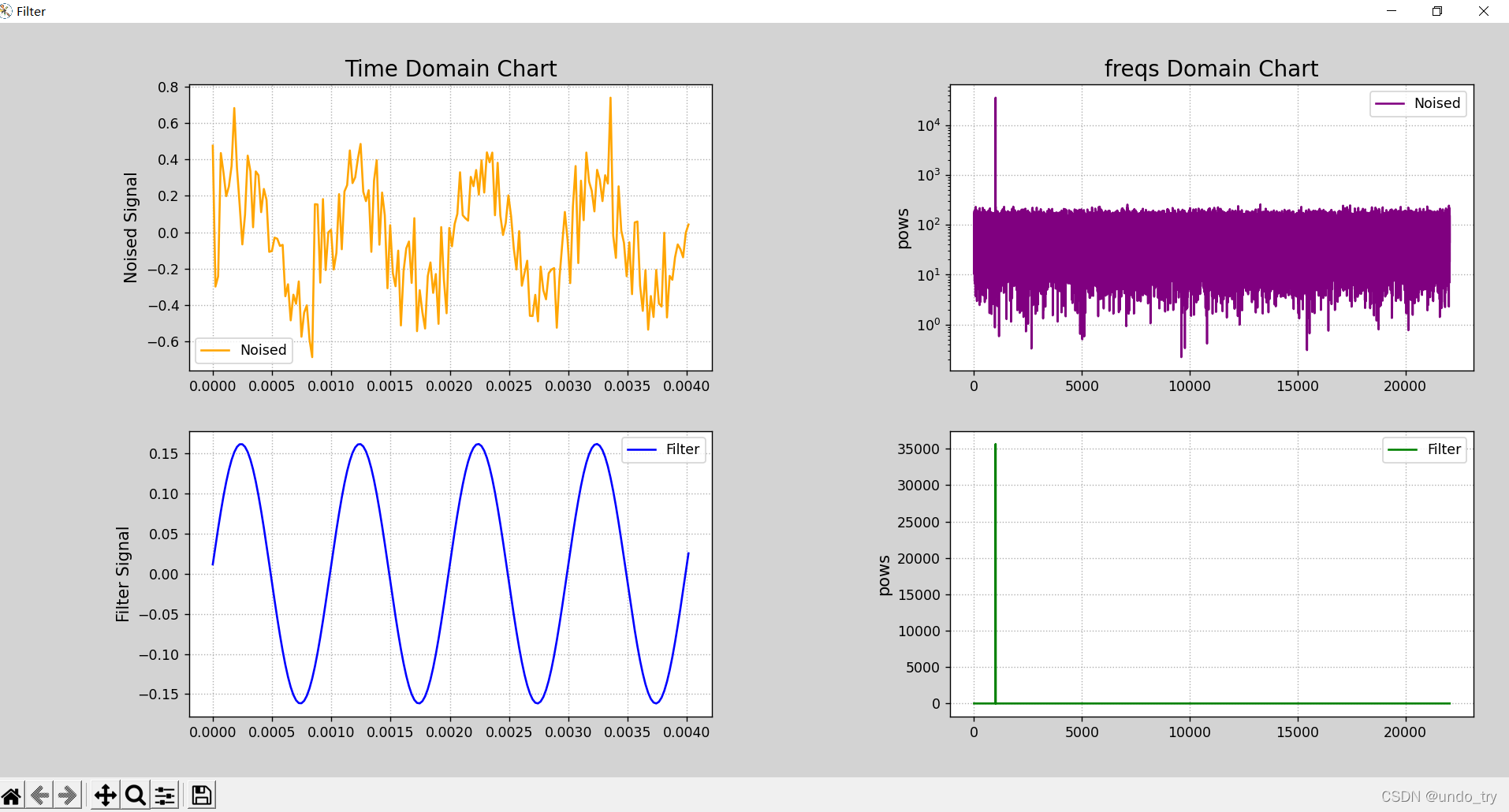
案例:基于傅里叶变换的频域滤波为音频文件去除噪声。
"""
频率滤波降噪
"""
import numpy as np
import numpy.fft as nf
import scipy.io.wavfile as wf
import matplotlib.pyplot as mp
# 采样率(每秒采样点的个数) 以及 采样位移
sample_rate, noised_sigs = wf.read("D:\\python\\...\\noised.wav")
print(sample_rate, noised_sigs.shape)
noised_sigs = noised_sigs / 2 ** 15
# 1、绘制音频时域的:时间/位移图像。
times = np.arange(noised_sigs.size) / sample_rate
print(times)
mp.figure('Filter',facecolor='lightgray')
mp.subplot(221)
# 设置该图的题目
mp.title('Time Domain Chart',fontsize = 16)
mp.ylabel('Noised Signal',fontsize = 12)
mp.grid(linestyle=':')
mp.plot(times[:178],noised_sigs[:178],color='orange',label='Noised')
mp.legend()
mp.tight_layout()
# 2、基于傅里叶变换,获取音频频域信息,绘制音频频域的:频率/能量图像。
freqs = nf.fftfreq(times.size, times[1] - times[0])
complex_ary = nf.fft(noised_sigs)
pows = np.abs(complex_ary)
mp.subplot(222)
# 设置该图的题目
mp.title('freqs Domain Chart',fontsize = 16)
mp.ylabel('pows',fontsize = 12)
mp.grid(linestyle=':')
mp.semilogy((freqs[freqs > 0]),(pows[freqs > 0]),color='purple',label='Noised')
mp.legend()
mp.tight_layout()
# 3、将低频噪声去除后绘制音频频域的:频率/能量图像。
# 先找到能量最大的正弦函数的频率
found_freq = freqs[pows.argmax()]
# 然后找出噪声的下标
noised_index = np.where(freqs != found_freq)
# 把噪声位置的复数数据设置为0
complex_ary[noised_index] = 0
pows = np.abs(complex_ary)
mp.subplot(224)
# 设置该图的题目
mp.ylabel('pows',fontsize = 12)
mp.grid(linestyle=':')
mp.plot((freqs[freqs > 0]),(pows[freqs > 0]),color='green',label='Filter')
mp.legend()
# 4、基于逆向傅里叶变换,生成新的音频信号,绘制音频时域的:时间/位移图像。
filter_sigs = nf.ifft(complex_ary).real
mp.subplot(223)
# 设置该图的题目
mp.ylabel('Filter Signal',fontsize = 12)
mp.grid(linestyle=':')
mp.plot(times[:178],filter_sigs[:178],color='blue',label='Filter')
mp.legend()
mp.tight_layout()
# 重新生成音频文件。
wf.write("D:\\python\\video\\笔记\\第五阶段\\AI\\data_note\\素材\\da_data\\filter_noised.wav", sample_rate,
(filter_sigs * 2 ** 15).astype(np.int16) )
mp.show()