开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 机器学习（十）偏差和方差问题 -> 正文阅读

[人工智能]机器学习（十）偏差和方差问题

文章目录

- Log
一、决定下一步做什么（Deciding what to try next）
- 1. 关注的问题
- 2. 改进算法性能的方法
二、评估假设（Evaluating a hypothesis）
三、模型选择和训练、验证、测试集（Model selection and training/validation/test sets）
四、诊断偏差与方差（Diagnosing bias vs. variance）
- 1. 偏差与方差
- 2. 判断方法
五、正则化和偏差方差（Regularization and bias/variance）
六、学习曲线（Learning curves）
七、决定接下来做什么（Deciding what to try next【revisited】）
- 1. 如何判断哪些方法有效
- 2. 以上内容与神经网络的联系
总结

应用机器学习时的建议——advice for applying machine learning

Log

2022.01.25开始学习第十章
2022.01.26继续学习
2022.01.27明天弄完
2022.01.28结束第十章

一、决定下一步做什么（Deciding what to try next）

本篇文章将要介绍一些实用的建议和指导，帮助我们明白怎样进行选择。

1. 关注的问题

将要重点关注的问题是：在开发一个机器学习系统（或者试着改进一个机器学习系统的性能）时，应该如何决定接下来应该选择哪条道路。
为了解释这一问题，仍然使用预测房价的学习例子，假设已经完成了正则化线性回归（也就是最小化代价函数 J 的值）
$\begin{aligned} J(θ)=\frac{1}{2m}[\sum_{i=1}^m(h_θ(x^{(i)})-y^{(i)})^2+λ\sum_{j=1}^nθ_j^2] \end{aligned}$

2. 改进算法性能的方法

假如在得到学习参数以后，如果将假设函数放到一组新的房屋样本上进行测试。如果发现在预测房价时产生了巨大的误差，现在的问题就是要改进这个算法，接下来应该怎么办。实际上可以想出很多种方法来改进这个算法的性能：
$\begin{aligned} &-Get\ \ more\ \ training\ \ examples\\ &-Try\ \ smaller\ \ sets\ \ of\ \ features\\ &-Try\ \ getting\ \ additional\ \ features\\ &-Try\ \ adding\ \ polynomial\ \ features(x_1^2,x_2^2,x_1x_2,etc.)\\ &-Try\ \ decreasing\ \ \lambda\\ &-Try\ \ increasing\ \ \lambda\\ \end{aligned}$
1. 使用更多的训练样本：
  可以通过电话调查或上门调查来获取更多的不同的房屋出售数据，但有时候获得更多的训练数据，实际上并没有作用，有时应该避免把时间浪费在收集更多的训练数据上。
2. 尝试选用更少的特征：
  从所有特征中仔细挑选一小部分，来防止过拟合。
3. 尝试选用更多的特征：
  在确定选用的特征之前需要先明确这样做是否有效，因为接下来将会花费大量的时间来收集相关的数据。
4. 尝试增加多项式特征
5. 减小或增大正则化参数 λ 的值
有许多人在进行下一步时随意地选择上述方法中的一种，但是在实现了所选方法之后却发现这个方法的效果并不好。
实际上，有一系列简单的方法可以使我们快速地排除掉上面的单子上至少一半不太有效的方法，从而节省大量不必要花费的时间。
下面的几个部分中，首先介绍怎样评估机器学习算法的性能，然后在后面的几小节中开始讨论这些方法，被称为机器学习诊断法（machine learning diagnostics）。
诊断法：通过执行测试来了解算法在哪里出了问题的一种测试法。
（通常也能告诉我们，要想改进一种算法的效果，什么样的尝试才是有意义的）

二、评估假设（Evaluating a hypothesis）

本节将要介绍怎样评价算法学习得到的假设，基于本节的内容，后续还会展开讨论如何防止过拟合和欠拟合的问题。

1. 过拟合问题

当我们确定学习算法的参数时，考虑的是选择参数来使训练误差最小化，但是并不能因为假设具有很小的训练误差来断定他是一个好的假设，比如过拟合假设的例子，此时推广到新的训练样本上就不好使了。
对于下面简单的例子，可以画出假设函数，然后观察图像，判断是否发生过拟合。
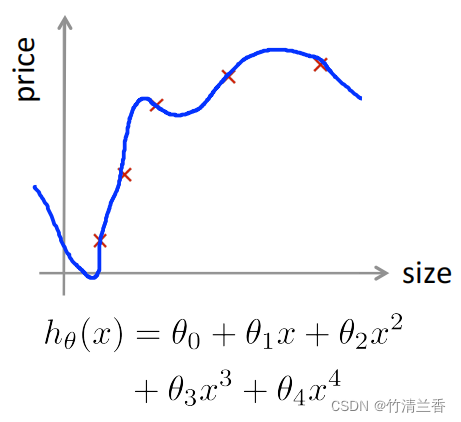
但对于一般的情况，特征不止一个的例子，想要通过画出假设函数的图像来观察就变得很难甚至不可能了，因此，需要另一种评价假设函数的方法。

2. 数据分割

假设有这样一组的数据，下面只展示十组训练样本，为了确保可以评价假设函数，需要将这些数据分为两部分，一部分作为训练集，另一部分作为测试集。
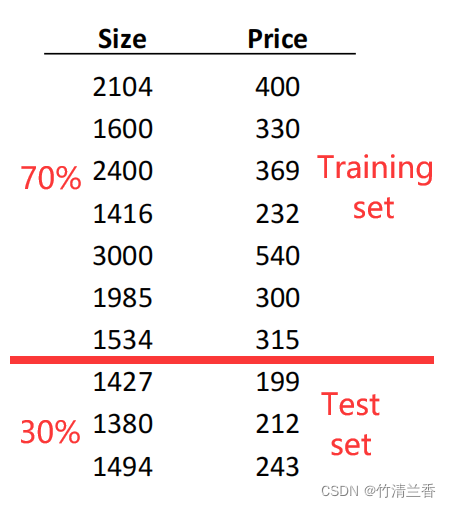
将所有数据分成训练集和测试集的一种典型的分割方法，是按照 7:3 的比例进行分割，70%的数据作为训练集，30%的数据作为测试集。
定义如下符号：
$\begin{aligned} &\textbf{Training\ \ set:}\\ &\qquad (x^{(1)},y^{(1)})\\ &\qquad(x^{(2)},y^{(2)})\\ &\qquad\quad\ \ \ ...\\ &\qquad(x^{(m)},y^{(m)})\\\ \\ &\qquad(m\ 依然表示\textbf{训练}样本的总数 )\\ &\textbf{Test\ \ set:}\\ &\qquad (x^{(1)}_{tset},y^{(1)}_{tset})\\ &\qquad(x^{(2)}_{tset},y^{(2)}_{tset})\\ &\qquad\qquad...\\ &\qquad(x^{(m_{tset})}_{tset},y^{(m_{tset})}_{tset})\\\ \\ &\qquad(m_{tset}\ 表示\textbf{测试}样本的总数)\\ &\qquad(样本的下标\ test\ 表示这些样本来自测试集)\\ \end{aligned}$
注意： 如果数据不是随机排列的，需要先将其打乱顺序，再进行数据的分割（或者使用一种随机的顺序来构建数据）。

3. 训练和测试的步骤

下面展示了一种典型的方法来训练和测试学习算法：

①线性回归

训练和测试线性回归的步骤：
1. 最小化训练误差（对训练集进行学习得到参数 θ）。这里的 J(θ) 是使用70%的数据来定义得到的训练数据
2. 计算测试误差。用 J_test 来表示测试误差，把从训练集中学习得到的参数代到下面的表达式（实际上是测试集平方误差的平均值）中来计算测试误差

$\begin{aligned} &-Learn\ \ parameter\ \ \theta\ \ from\ \ training\ \ data\ \ (minimizing\\\ \ &\quad \ training\ \ error\ \ J(\theta))\ \ \\ &-Compute\ \ test\ \ set\ \ error:\\ &\qquad\large J_{test}(\theta)=\frac{1}{2m_{test}}\sum^{m_{test}}_{i=1}(h_\theta(x^{(i)}_{test})-y^{(i)}_{test})^2 \end{aligned}$

②逻辑回归

训练和测试逻辑回归的步骤：
- 首先要从训练数据学习得到参数
- 然后用如下的方式计算测试误差，目标函数和平常做逻辑回归的一样，唯一的区别是现在使用的是测试样本，这里的测试误差的定义非常合理，还有另一种形式的测试度量，可能更易于理解，叫做错误分类（misclassification error），也被称为 0/1 分类错误，0/1 表示了预测的分类是正确或错误的情况。
- 下一个式子就是使用 0/1 错误分类度量来定义的测试误差（misclassification metric）。

$\begin{aligned} &-Learn\ \ parameter\ \ \theta\ \ from\ \ training\ \ data\\ &-Compute\ \ test\ \ set\ \ error:\\ &\qquad\large J_{test}(\theta)=-\frac{1}{m_{test}}\left[\sum^{m_{test}}_{i=1}(y^{(i)}_{test}logh_\theta(x^{(i)}_{test})+(1-y^{(i)}_{test})log(1-h_\theta(x^{(i)}_{test})))\right]\\\ \\ &-Misclassification\ \ error\ \ (0/1\ \ misclassification\ \ error):\\ &\qquad err(h_\theta(x),y)= \begin{cases} 1 &\text{if } \ \ h_\theta(x)\ge0.5\ \ \ \ \ \ \ \ \ \ y=0 \\ &\text{or\ \ if } \ \ \ h_\theta(x)<0.5\ \ \ \ y=1\\ 0 &\text{otherwise } \end{cases}\\\ \\ &\qquad Test\ \ error=\frac{1}{m_{test}}\sum^{m_{test}}_{i=1}err(h_\theta(x^{(i)}_{test}),y^{(i)}_{test}) \end{aligned}$

下面的一部分将要应用这些方法来帮助我们进行诸如特征选择一类的问题，比如学习算法，多项式次数的选择或者学习算法正则化参数的选择。

三、模型选择和训练、验证、测试集（Model selection and training/validation/test sets）

模型选择问题（model selection problems）： 怎样选用正确的特征来构造学习算法，来确定对于一个数据集最合适的多项式次数；或者如何选择学习算法中的正则化参数 λ。
在这一问题的讨论中，所说的不仅仅是如何把数据分为训练集和测试集，而是如何将数据分为三个数据组，也就是训练集（training set）、验证集（validation set） 和 测试集（test set）。
下面的部分中将会介绍上面这些内容的含义以及如何使用它们进行模型选择。

1. 过拟合问题

在过拟合的情况中，学习算法即便对训练集拟合的很好，也并不代表它是一个好的假设，一般来说，这就是为什么训练集误差不能用来判断该假设对新样本的拟合好坏。
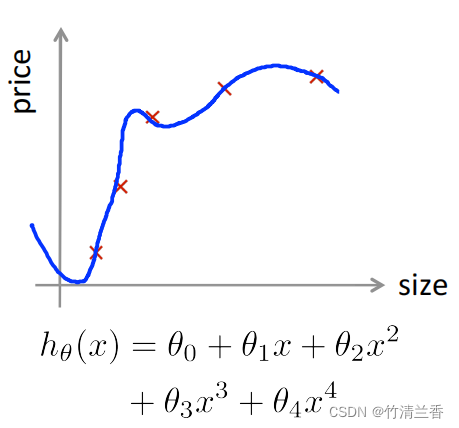
具体来讲，如果用这些参数（如 θ₀、θ₁、θ₂）来拟合训练集，即便假设在训练集上表现的很好，也并不意味着该假设对训练集中没有的新样本有多好的泛化能力。
更为普遍的规律是，如果你的参数对某个数据集拟合的很好（比如训练机或者其他数据集），那么用同一数据集计算得到的误差（比如训练误差），并不能很好地估计出实际的泛化误差，即该假设对新样本的泛化能力。

2. 模型选择问题

如何才能选择能最好的拟合数据的多项式次数（应该选择一次函数，二次函数，三次函数等等，一直到十次函数中的哪一个）？
这类似于在这个算法里加入一个参数，用 d 来表示应该选择的多项式次数。所以除了参数 θ，还有一个参数 d，需要用数据集来确定。
下面第一个选择是 d=1 表示线性函数，也可以选择 d=2、 d=3 等等，一直到 d=10。
$\begin{aligned} &(d=1)\ \ \ \ \ \ 1.\ \ h_\theta(x)=\theta_0+\theta_1x\\ &(d=2)\ \ \ \ \ \ 2.\ \ h_\theta(x)=\theta_0+\theta_1x+\theta_2x^2\\ &(d=3)\ \ \ \ \ \ 3.\ \ h_\theta(x)=\theta_0+\theta_1x+...+\theta_3x^3\\ &\qquad ...\\ &(d=10)\ \ 10.\ \ h_\theta(x)=\theta_0+\theta_1x+...+\theta_{10}x^{10}\\ \end{aligned}$

①确定模型

接下来想要确定这个多出来的参数 d，具体来说就是想要选择一个多项式的次数（从十个模型中选择一个），拟合这个模型，并且估计这个拟合好的模型假设对新样本的泛化能力。
$\begin{aligned} \theta^{(i)} \Rightarrow用 i 次函数拟合数据集得到的参数 \end{aligned}$
具体做法： 选择每一个模型，最小化训练误差，得到对应的参数向量，再对所有的模型求出测试集误差（就是取每一个假设和它相应的参数，然后计算出它在测试集的性能），选择具有最小的测试误差的一个作为最终的模型。
$\begin{aligned} &Model\ \ h_\theta(x)\ \ (d=i)(use\ \ training\ \ set)\\ \Rightarrow \ \ &\min\limits_\theta J(\theta)\\ \Rightarrow \ \ &\theta^{(i)}\Rightarrow (use\ \ test\ \ set)\\ \Rightarrow \ \ &J_{test}(\theta^{(i)})\\ \Rightarrow \ \ &Pick\ \ d=4\\ \end{aligned}$

②测定泛化能力（数据分割）

在测试选定的模型对新样本的泛化能力时，用测试集中的样本对测试集数据得到的模型（用测试集拟合了参数 d。计算 J_test 的时候已经使用了测试集，再检验泛化时已经无新数据可用了，即测试集不能既确定模型又评估模型的泛化能力）来验证是存在问题的，为了解决这一问题，通常采用如下的方法来评估一个假设：
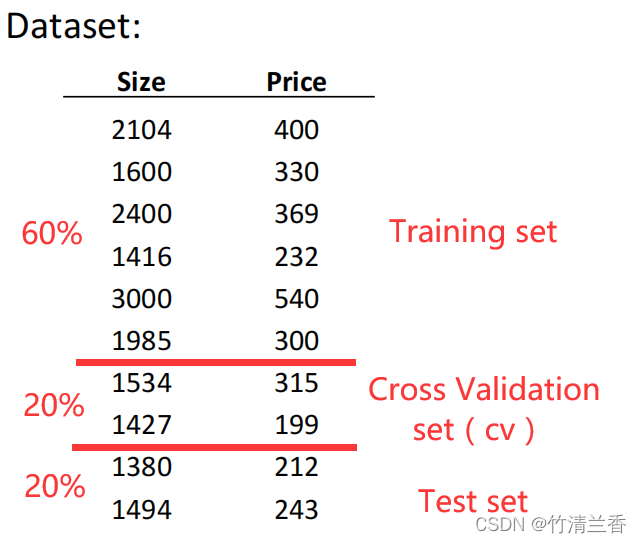
给定一个数据集，将其分为三个部分，分别是训练集（training set
）、交叉验证集（cross validation set）、测试集（test set
）。这些数据的典型分配比例是 6:2:2。
$\begin{aligned} &\textbf{Training\ \ set:}\\ &\qquad 样本：(x^{(m)},y^{(m)})\\ &\qquad 训练样本总数：m\\ &\textbf{Training\ \ set:}\\ &\qquad 样本：(x^{(m_{cv})}_{cv},y^{(m_{cv})}_{cv})\\ &\qquad 验证样本总数：m_{cv}\\ &\textbf{Test\ \ set:}\\ &\qquad 样本：(x^{(m_{tset})}_{tset},y^{(m_{tset})}_{tset})\\ &\qquad 测试样本总数：m_{tset}\\ \end{aligned}$
同样的也可以定义训练误差、交叉验证误差和测试误差：
$\begin{aligned} &\textbf{Training\ \ error: }\\ &\qquad\large J_{train}(\theta)=\frac{1}{2m}\sum^{m}_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2\\ &\textbf{Cross\ \ Validation\ \ error: }\\ &\qquad\large J_{cv}(\theta)=\frac{1}{2m_{cv}}\sum^{m_{cv}}_{i=1}(h_\theta(x^{(i)}_{cv})-y^{(i)}_{cv})^2\\ &\textbf{Test\ \ error:}\\ &\qquad\large J_{test}(\theta)=\frac{1}{2m_{test}}\sum^{m_{test}}_{i=1}(h_\theta(x^{(i)}_{test})-y^{(i)}_{test})^2\\ \end{aligned}$
用验证集来选择模型（而不是用原来的测试集）

$\begin{aligned} &Model\ \ h_\theta(x)\ \ (d=i)(use\ \ training\ \ set)\\ \Rightarrow \ \ &\min\limits_\theta J(\theta)\\ \Rightarrow \ \ &\theta^{(i)}\qquad\Rightarrow (use\ \ validation\ \ set)\\ \Rightarrow \ \ &J_{cv}(\theta^{(i)})\Rightarrow (use\ \ test\ \ set)\\ \Rightarrow \ \ &Pick\ \ d=4\\ \Rightarrow \ \ &Estimate\ \ generalizati\ \ on\ \ error\ \ for\ \ test\ \ set\ \ J_{test}(\theta^{(4)}) \end{aligned}$

具体做法： 首先选取一个假设模型（用训练集作为初始样本进行拟合），然后最小化代价函数，得到对应的参数向量 θ；然后再用交叉验证集来测试这些假设，计算出 J_cv 来观察这些假设模型在交叉验证集上的效果如何，选择交叉验证误差最小的那个假设作为选定的模型；最后用测试集来衡量（或者估计）算法选出的模型的泛化误差

四、诊断偏差与方差（Diagnosing bias vs. variance）

引言：当运行一个学习算法时，如果这个算法表现不理想，那么多半是出现两种情况：偏差较大或方差较大，即欠拟合问题或过拟合问题。这种情况下搞清楚是偏差问题还是方差问题，或者两者都有关十分重要，因为确定下来是哪种情况，就能很快找到有效的方法和途径来改进算法。
主要内容： 如何观察算法，然后判断是偏差问题（bias problem）还是方差问题（variance problem）（对于改进实际的学习算法的效果非常重要）。

1. 偏差与方差

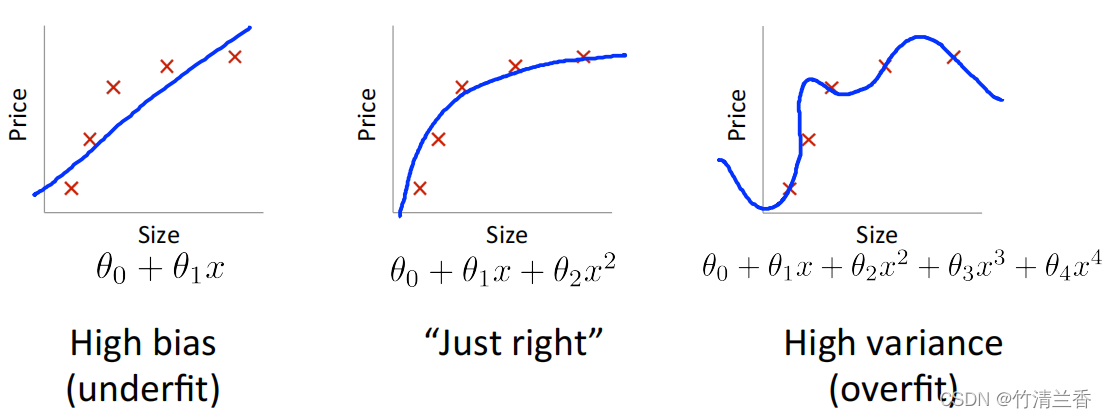
在这里插入图片描述

如果用简单的假设来拟合数据（比如说用一条直线）就会欠拟合（高偏差）；
如果用很复杂的假设来拟合时，可能会完美拟合训练集，但是会过拟合（高方差）；
中等复杂的假设（比如二次多项式的假设，次数既不高也不低）对数据拟合的刚刚好，此时对应的泛化误差也是三种情况中最小的。

2. 判断方法

沿用之前所使用的训练误差和验证误差的定义，分别是用训练集和交叉验证集计算的均方误差（average square error）。
$\begin{aligned} &\textbf{Training\ \ error: }\\ &\qquad\large J_{train}(\theta)=\frac{1}{2m}\sum^{m}_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2\\ &\textbf{Cross\ \ Validation\ \ error: }\\ &\qquad\large J_{cv}(\theta)=\frac{1}{2m_{cv}}\sum^{m_{cv}}_{i=1}(h_\theta(x^{(i)}_{cv})-y^{(i)}_{cv})^2\\ \end{aligned}$
横坐标表示多项式的次数，越往右多项式的次数越大。随着多项式次数的增大，我们对于训练集的拟合效果也越来越好，训练误差明显下降；通过前面的内容我们可以知道，中等复杂的假设对数据拟合的刚刚好，因此交叉训练误差先减小后增大。

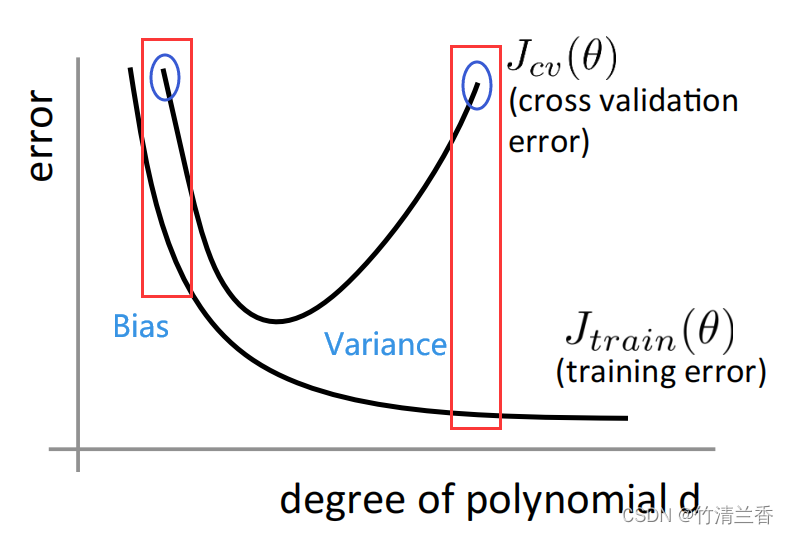
在这里插入图片描述

如果交叉验证误差或者测试集误差都很大，如何判断此时的学习算法出现了高偏差的问题，还是高方差的问题？
交叉验证误差比较大的情况对应着曲线中的左边和右边。
靠左的一端对应的是高偏差问题（使用了过小的多项式次数），
右边的一端对应的是高方差问题（多项式的次数对数据来说过大）。
具体的区分方法：
- 对于高偏差的情况（欠拟合），交叉验证误差和训练误差都很大；
- 对于高方差问题，训练误差会很小（代表对训练级数据拟合的很好），交叉验证误差会远大于训练集误差。
  $\begin{aligned} &\textbf{Bias(underfit):}\\ &\qquad J_{train}(\theta)\ \ will\ \ be\ \ high\\ &\qquad J_{cv}(\theta)\approx J_{train}(\theta)\\\ \\ &\textbf{Variance(overfit):}\\ &\qquad J_{train}(\theta)\ \ will\ \ be\ \ low\\ &\qquad J_{cv}(\theta)\gg J_{train}(\theta)\\ \end{aligned}$

五、正则化和偏差方差（Regularization and bias/variance）

主要内容： 之前学到算法正则化可以有效的防止过拟合，下面将介绍正则化和算法的偏差与方差的关系，以及正则化是如何影响偏差和方差的。

1. 不同程度大小正则化参数对应的情况

假如要对下面的这个高阶多项式进行拟合，为了防止过拟合，将要使用正则化，通过一个正则化项来让参数的值尽量的小：

$\begin{aligned} &\textbf{Model:}\\ &\qquad h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3+\theta_4x_4^4\\ &\textbf{Learning\ \ algorithm\ \ objective :}\\ &\qquad J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_θ(x^{(i)})-y^{(i)})^2+\red{\frac{λ}{2m}\sum_{j=1}^nθ_j^2} \end{aligned}$

然后分析下面三种情形：

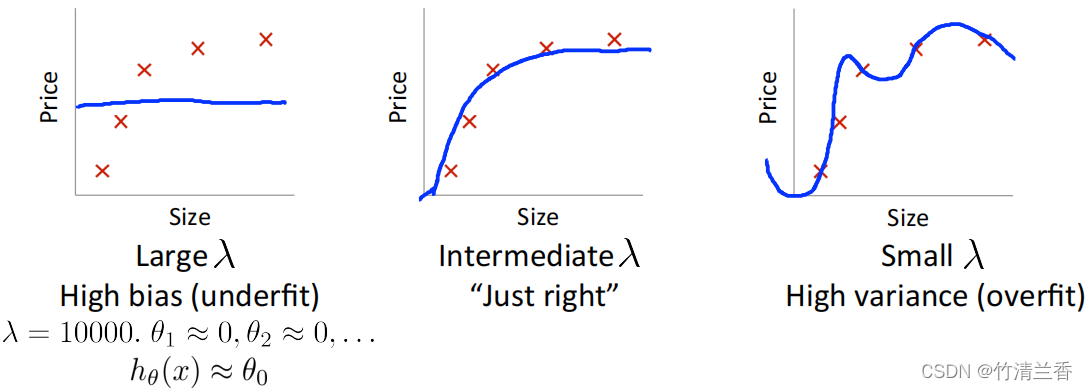
第一种情形（上图左）是非常大的正则化参数 λ（比如 λ 取 10000 或者其他比较大的值），在这种情况下，所有这些参数包括 θ₁、θ₂、θ₃ 等等将被惩罚很重。其结果是这些参数大部分都接近于零，并且这个假设 h(x) 将等于或近似等于 θ₀。因此，最终得到的假设函数大致近似是一条水平的直线。
另一种极端的情况（上图右）是，如果有非常小的 λ，比如说等于 0，在这种情况下，如果要拟合一个高阶多项式的话，通常会出现过拟合的情况；如果没有进行正则化或者正则化程度很小的话，通常会得到高方差（过拟合）的结果，因为通常来说的值等于零，相当于没有正则化，因此会对假设过拟合。
只有当我们取一个大小适中、既不大也不小的值时（上图中），才能得到一组对数据拟合比较合理的参数值

2. 如何自动选择出一个最适合的正则化参数

①定义：训练集、交叉验证集以及测试集误差

假设在使用正则化的情形中，定义 J_train(θ) 为另一种不同的形式，即把它定义为最优化目标（the optimization objective），去掉正则化项：
$\begin{aligned} &J_{train}(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_θ(x^{(i)})-y^{(i)})^2 \end{aligned}$
注：
在前面没有使用正则化时定义的 J_train(θ) 就是代价函数 J(θ)；
当使用了正则化（添加了 λ 项）时，就将训练集误差 J_train(θ) 定义为训练集的平方误差之和（训练集上平均的平方误差），不考虑正则化项。
类似地也定义交叉验证集误差，以及测试集误差：
$\begin{aligned} &J_{cv}(\theta)=\frac{1}{2m_{cv}}\sum_{i=1}^{m_{cv}}(h_θ(x^{(i)}_{cv})-y^{(i)}_{cv})^2\\ &J_{test}(\theta)=\frac{1}{2m_{test}}\sum_{i=1}^{m_{test}}(h_θ(x^{(i)}_{test})-y^{(i)}_{test})^2\\ \end{aligned}$
这三者的定义都是平均的误差平方和，或是不使用正则化项式的训练集、验证集和测试集的平均的误差平方和的一半。

②自动选择正则化参数 λ 的方法（模型选择在选取正则化参数时的应用）

选取一系列想要尝试的值，通常将步长设为二倍速度增长直到一个比较大的值，对于本例选取 12 个不同的备选模型，对应了 12 个不同的正则化参数 λ：
$\begin{aligned} 1.& \quad Try\ \ \lambda = 0\\ 2.& \quad Try\ \ \lambda = 0.01\\ 3.& \quad Try\ \ \lambda = 0.02\\ 4.& \quad Try\ \ \lambda = 0.04\\ 5.& \quad Try\ \ \lambda = 0.08\\ &\qquad ...\\ 12.& \quad Try\ \ \lambda = 10\ \ (10.24)\\ \end{aligned}$
实现步骤：
- 选用每一个模型，然后最小化代价函数 J(θ)，得到某个参数向量 θ
- 接下来用所有这些假设、参数、交叉验证集来评价他们，然后选取 12 个模型中交叉验证集误差最小的那个模型作为最终选择（例如最终选择第 5 个模型）；
- 最后，如果想知道该模型的测试误差，可以用选出来的 θ⁽⁵⁾，然后观察他在测试集上的表现。

$\begin{aligned} Model\Longrightarrow \min\limits_\theta J(\theta)\Longrightarrow \theta^{(i)}\Longrightarrow J_{cv}(\theta^{(i)})\Longrightarrow J_{test}(\theta^{(5)}) \end{aligned}$

③交叉验证误差和训练误差随正则化参数 λ 的变化图像

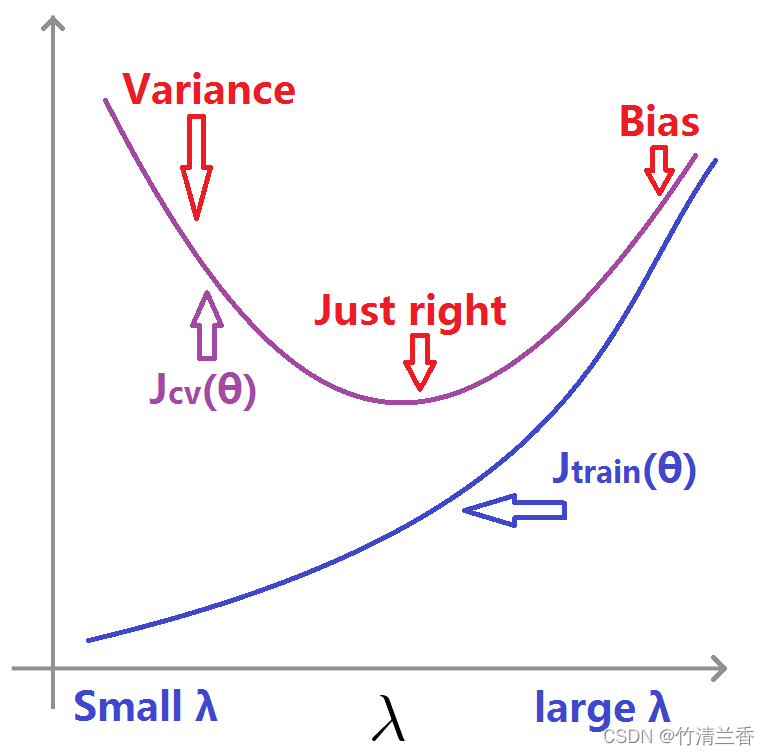
在这里插入图片描述

当 λ 较小时，相当于没有使用正则化，容易发生过拟合，此时，对于训练集拟合相对较好，得到比较小的 J_train(θ) ，交叉验证集的误差也会很大；
当 λ 过大时，容易产生高偏差问题，不能对训练集很好地拟合，对应的 J_train(θ) 比较大，交叉验证集的误差也会很大。
因此 J_train(θ) 的曲线呈上升趋势， J_cv(θ) 的曲线两端高中间低，先下降后上升。
总会有中间的某个值，表现的刚好合适，此时的交叉验证误差和测试误差都很小。
说明： 上图的曲线，偏向于简单和理想化，对于真实的数据得到的曲线可能更凌乱，会有更多的噪声，但是趋势都是类似的。

$\begin{aligned} &J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_θ(x^{(i)})-y^{(i)})^2+\red{\frac{λ}{2m}\sum_{j=1}^nθ_j^2}\\ &J_{train}(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_θ(x^{(i)})-y^{(i)})^2\\ &J_{cv}(\theta)=\frac{1}{2m_{cv}}\sum_{i=1}^{m_{cv}}(h_θ(x^{(i)}_{cv})-y^{(i)}_{cv})^2\\ \end{aligned}$

补充理解： 用 J(θ)（包含正则化项）来求 θ，然后为了比较 λ 对 θ 的影响，用 J_train(θ) 和 J_cv(θ) 绘制曲线（不包含正则化项）。实际上训练时用的是 J(θ)，而 J_train(θ) 和 J_cv(θ) 只是用来画线说明问题。

六、学习曲线（Learning curves）

学习曲线可以用来检查算法运行是否一切正常或者改进算法的表现，是否处于偏差方差问题或是二者皆有。

1. 绘制学习曲线

先绘制出训练集的平均误差平方和，或者交叉验证集的平均误差平方和关于参数 m 的函数，也就是一个关于训练集样本总数的函数。
比如有100组训练样本，首先人为地减小训练集，然后对于这些小的训练集画出训练集误差以及交叉验证集误差。
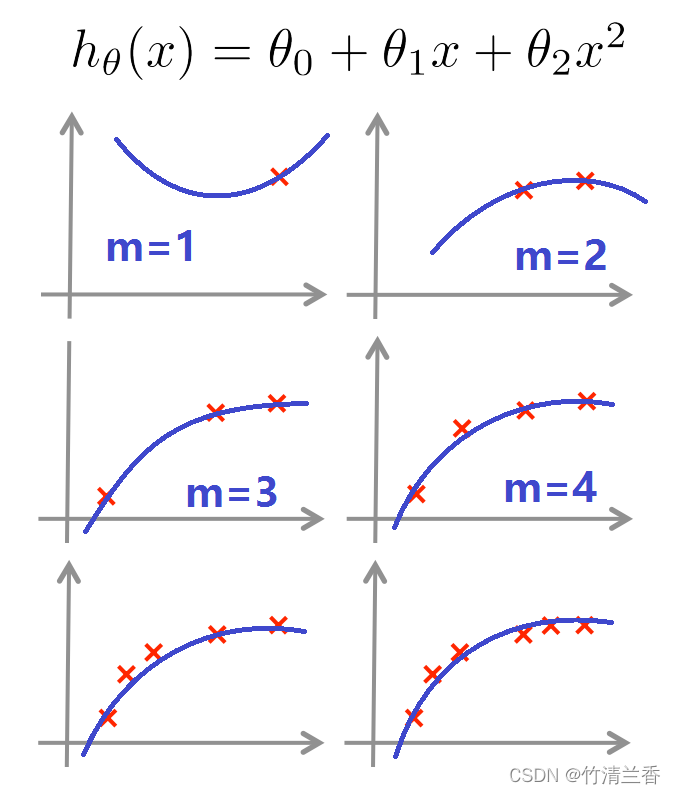
当训练样本容量 m 很小的时候，训练误差也会很小，此时能把训练集拟合的非常好，当训练集越来越大的时候，要保证使用二次函数对所有样本的拟合效果依然很好，就越来越困难了。
事实上随着训练机容量的增大，平均训练误差在增大，对应图像中训练集误差随 m 增大而增大。
交叉验证误差就是在没有见过的交叉验证集上的误差，当训练集很小的时候，泛化程度不会很好，不能很好的适应新样本，此时对应的假设并不是一个理想的假设，只有当时用一个更大的训练集时，才有可能得到一个能够更好拟合数据的假设。
因此，验证集误差和测试集误差都会随着训练集样本容量m的增加而减小，因为使用的数据越多，越能获得更好的泛化表现，所以数据越多越能拟合出合适的假设，对应的和图像如下：

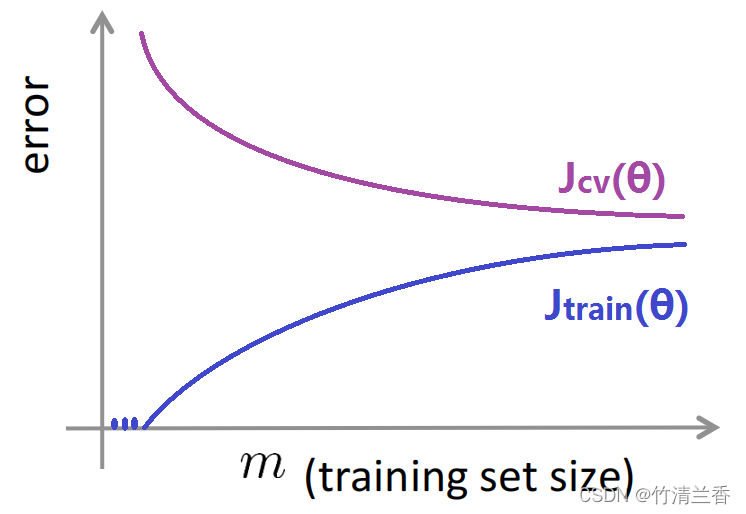
2. 不同情况下的学习曲线

①高偏差情况下的学习曲线

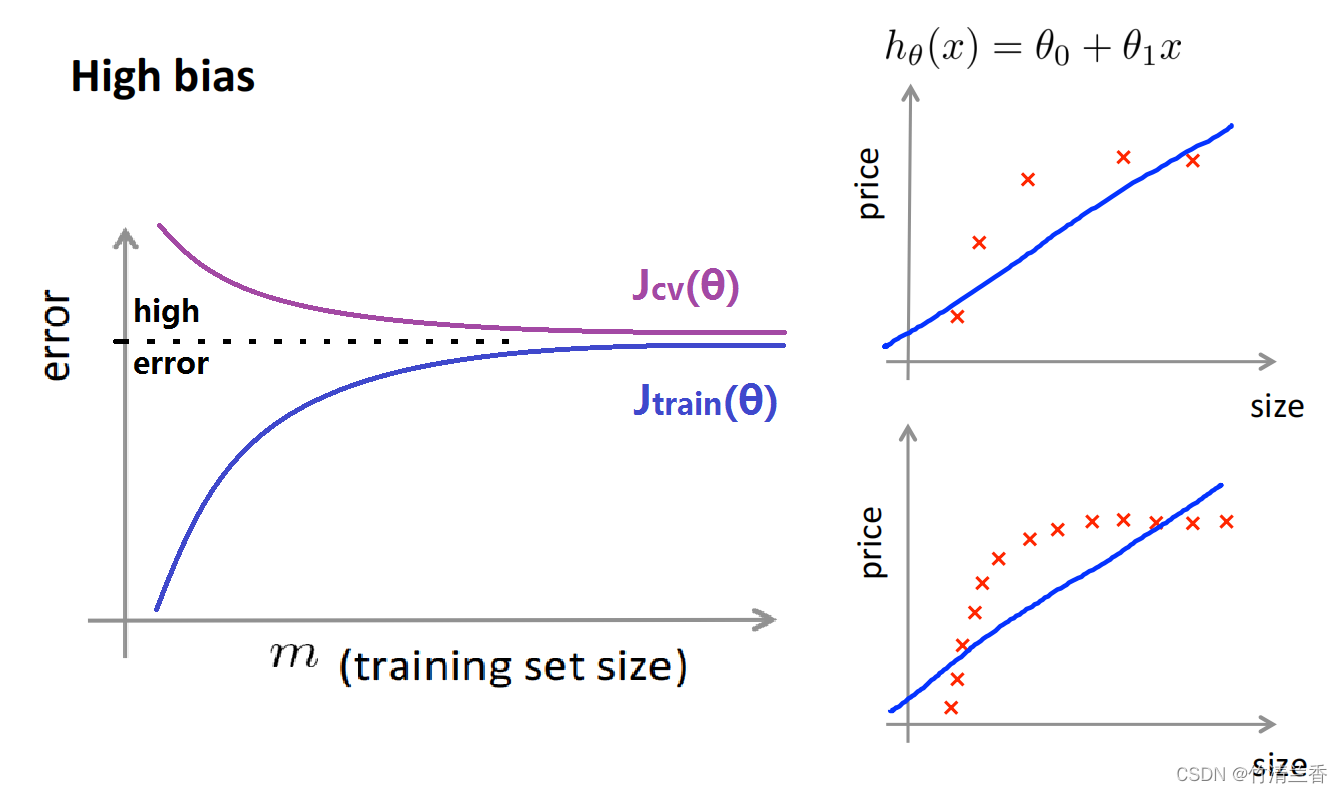
在这里插入图片描述

用一条直线拟合数据来说明问题
把样本容量扩大后，最后得到的仍然是类似的一条直线，因为一条直线并不能很好的拟合上面的情况，所以即使样本容量扩大，直线也不会发生太大变化。
交叉验证集误差在训练集样本容量很小时表现的很不好，当训练集样本数增大到到某个值的时候，就会找到最有可能拟合数据的那条直线，此时继续增大训练集的样本容量，还是会得到一条差不多的直线，因此，交叉验证误差将会很快变为水平而不再变化。
训练误差一开始是很小的，在高偏差的情况中，训练误差会逐渐增大，最后接近交叉验证误差，因为参数很少又有很多数据，当 m 很大的时候，训练集和交叉验证集的误差将会非常接近。
高偏差的问题可以由很高的交叉验证误差和训练误差反映出来，也就是说，最终会得到一个值比较大的 J_train(θ) 和 J_cv(θ) 。
进一步得出一个结论，如果一个学习算法有高偏差，随着增加训练样本，交叉验证误差不会明显下降，基本变成水平，所以如果学习算法正处于高偏差的情形，那么选用更多的训练集数据对于改善算法表现无益。因此，判断算法是否正处于高偏差，可以避免把时间浪费在收集更多的训练数据上。

②高方差情况下的学习曲线

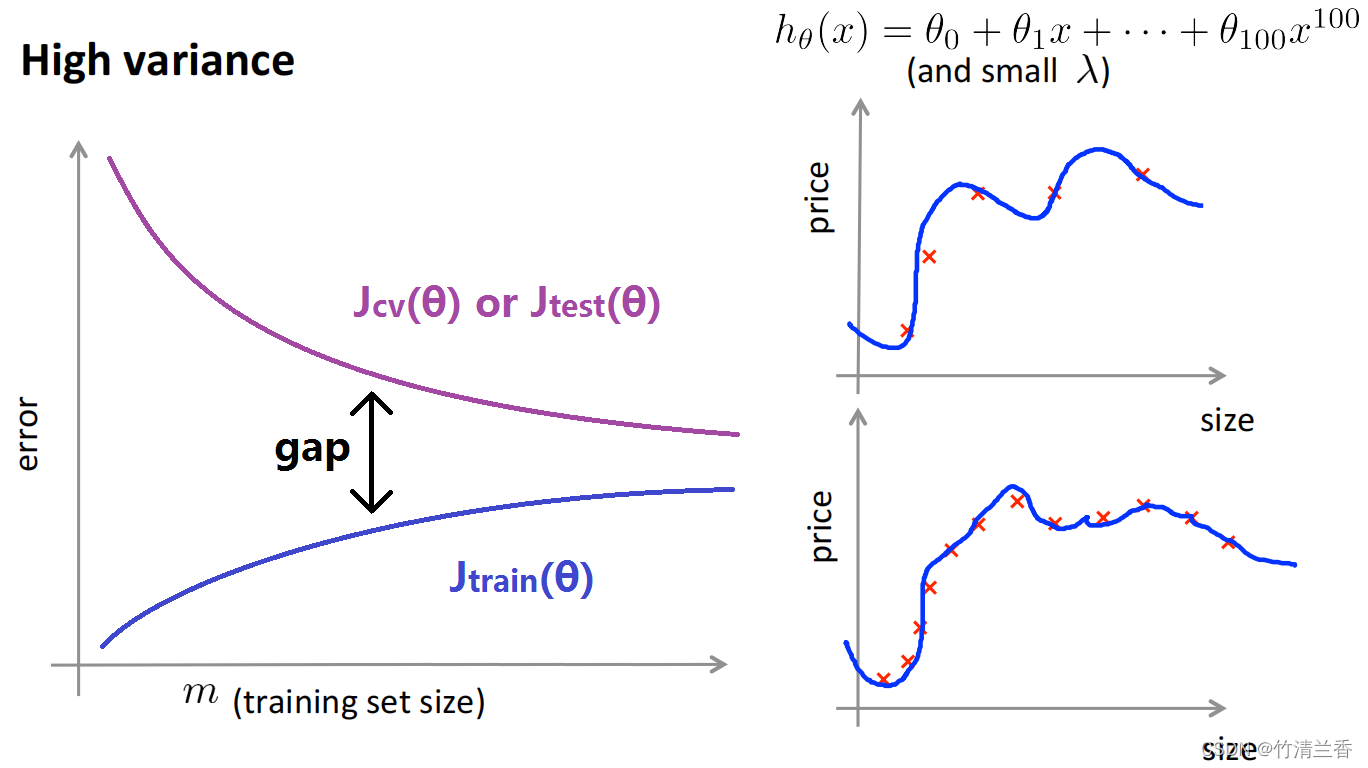
在这里插入图片描述

如果训练集很小（比如只有五个训练样本）同时用含高次的多项式来拟合（比如用100次的多项式函数），并且假设使用一个很小的 λ，最终会对这组数据拟合的很好，并且这个函数会对数据过拟合，此时的训练误差 J_train(θ) 会很小。随着训练样本容量的增加，可能仍然会有些过拟合，但是此时要对数据很好的拟合会变得更加困难。
J_train(θ) （训练误差）的值会随着训练集样本容量的增大而增大，因为当训练样本越多的时候就越难把训练集数据拟合的很好，但总的来说训练集误差还是很小的。
交叉验证误差将会一直都很大，即便是选择一个中等大小的训练样本数量。
所以算法处于高方差情形最明显的一个特点是在训练误差和交叉验证误差之间有一段很大的差距。
如果继续增大训练样本的数量（继续延伸曲线），交叉验证误差将会一直下降，所以在高方差的情形中使用更多的训练集数据，对于改进算法是有帮助的，可以告诉我们可能有必要花时间来增加更多的训练集数据。

七、决定接下来做什么（Deciding what to try next【revisited】）

主要内容： 学习曲线如何指引我们采取或者不采取某些方法来改进学习算法。
回到最开始试图用正则化的线性回归拟合模型，发现并没有达到我们预期的效果，提出了以下选择：
$\begin{aligned} &-Get\ \ more\ \ training\ \ examples\\ &-Try\ \ smaller\ \ sets\ \ of\ \ features\\ &-Try\ \ getting\ \ additional\ \ features\\ &-Try\ \ adding\ \ polynomial\ \ features(x_1^2,x_2^2,x_1x_2,etc.)\\ &-Try\ \ decreasing\ \ \lambda\\ &-Try\ \ increasing\ \ \lambda\\ \end{aligned}$

1. 如何判断哪些方法有效

使用更多的训练样本：
这种方法对于解决高方差问题是有帮助的。如果想要选择这种方法，应该先画出学习曲线，并且发现发现模型至少有那么一点方差问题（交叉验证误差应该比训练误差大一点）。
尝试选用更少的特征：
用更少的特征这种方法同样是对高方差时有效，换句话说，如果通过绘制学习曲线或者别的方法看出模型处于高偏差问题，就应该立即试图从已有的特征中挑出一小部分来使用，把时间用在刀刃上。
尝试选用更多的特征：
通常增加特征是解决高偏差问题的一个方法。对应情况产生的通常是因为当前的假设太简单，因此，想要更多的特征来使假设更好地拟合训练集。
尝试增加多项式特征
增加多项式特征实际上也是属于增加特征，因此这是另一种修正高偏差问题的方式。
减小正则化参数 λ 的值
解决高偏差问题
减小正则化参数 λ 的值
解决高方差问题

2. 以上内容与神经网络的联系

主要内容： 一些实用的经验，如何为神经网络模型选择结构或者连接形式。
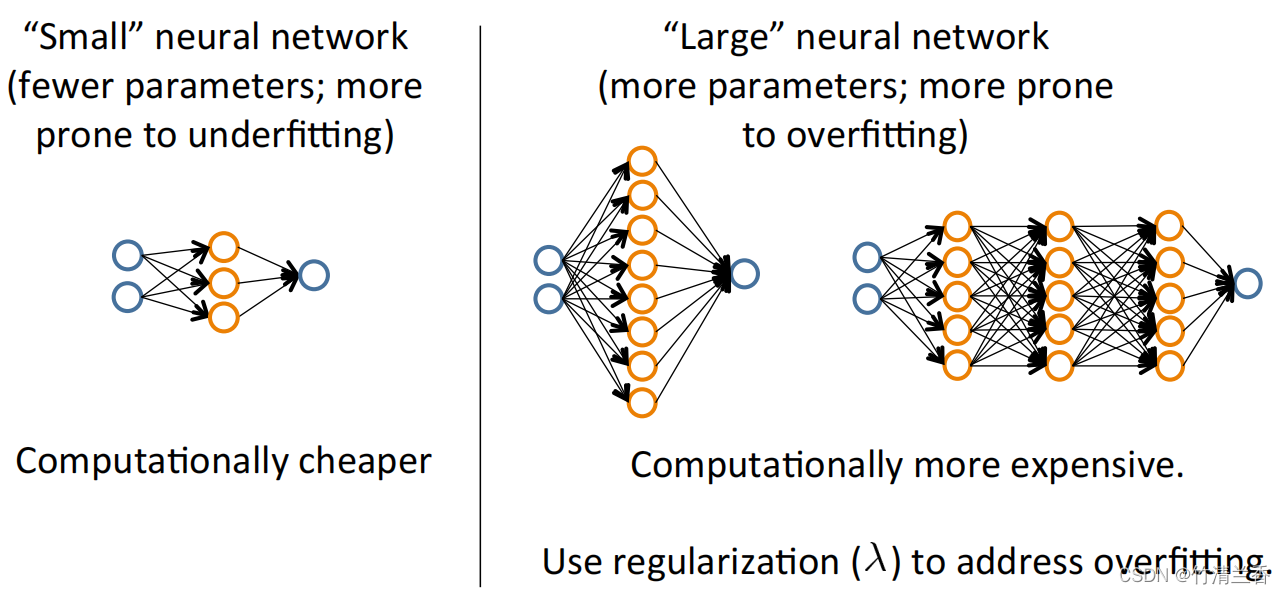
在进行神经网络拟合的时候，可以选择一个相对比较简单的神经网络模型，比如只有很少甚至只有一个隐含层，并且只有少量的隐含单元，像这样简单的神经网络参数不会很多，容易出现欠拟合。这种比较小型的神经网络最大的优势在于计算量较小。
与之相对的一种情况是，拟合较大型的神经网络结构，比如每一层的隐含单元数很多，或者有很多个隐含层，这种比较复杂的神经网络参数一般较多，更容易出现过拟合。这种结构的一大劣势就是当网络有大量神经元时这种结构会有很大的计算量，最主要的潜在问题还是更容易出现过拟合现象，实际上，越大型的网络性能越好，但如果发生了过拟合，可以使用正则化的方法来修正。
一般来说，使用一个大型的神经网络，并且使用正则化来修正过拟合问题，通常比使用一个小型的神经网络效果更好，但主要可能出现的一个问题就是计算量相对较大。
最后还需要选择需要的隐含层的层数，使用一个隐含层是比较合理的默认选项，但是如果想要选择一个最适合的隐含层层数，也可以尝试把数据分割为训练集、验证集和测试集，然后训练不同隐含层的神经网络，选出在交叉验证集上表现的最理想的神经网络模型（计算每一个模型的交叉验证误差 J_cv(θ) ）。

总结

本篇文章主要介绍一些了实用的建议和指导，帮助我们明白怎样进行选择。
主要介绍了偏差和方差问题以及判断这些问题用的方法（比如学习曲线）以及这些概念的含义，哪些方法对于改进学习算法是有帮助的，哪些是徒劳的。
首先提供了一些可以改进算法性能的方法。
随后在评估假设中通过将数据集分割成两部分来进行训练和测试（训练集，测试集【6:4】）。
在模型选择问题中通过将数据集分割成三部分来进行训练和测试（训练集，交叉验证集，测试集【6:2:2】）。
在诊断偏差与方差中，通过交叉验证误差和训练误差在不同多项式次数下的大小关系来区分高偏差和高方差。实际上偏差问题对应之前学过的欠拟合问题，方差问题则对应着过拟合问题。
在正则化和偏差方差中，为了进一步解决过拟合问题，选择对模型进行正则化处理，其中的关键就是确定合适的正则化参数大小，实现方法就是按照一定的步长选取一系列的参数，随后通过训练检测对应的模型从所有的模型中选出最合适的，进而确定正则化参数 λ 。
学习曲线可以用来检查算法运行是否一切正常或者改进算法的表现，是否处于偏差方差问题或是二者皆有。
最后回顾了开始提到的几种方法，进一步对其进行区分，介绍了每一种方法适用的情况，同时也简述了偏差和方差问题以及判断这些问题用的方法与神经网络的关系。