DQN介绍
DQN(Deep Q-Learning)是将深度学习与强化学习相结合,当Q-table他过于庞大无法建立的话,使用DQN是一种很好的选择。
DQN算法主要使用经历回放(experience replay)(经验池)来实现价值函数的收敛。
使用Deep Q-learning方法,从每一episode中得到的奖励来迭代更新Q(s,a). DQN算法中,(具体方法后续更出)继将每一个episode中使用的(s,a,r,a’)存储于M中,再从M中抽取mini-batch转换来最小化损失函数。
其具体做法是:
- 个体能够记住既往的状态转换经历,对于每一个完整状态序列里的每一次状态转换,依据当前状态的 S t \begin{array}{c} S_{t} \end{array} St??价值以贪婪策略选择一个行为 a t \begin{array}{c} a_{t} \end{array} at??,执行该行为得到奖励 R t + 1 \begin{array}{c} R_{t+1} \end{array} Rt+1??和下一个状态 S t + 1 \begin{array}{c} S_{t+1} \end{array} St+1??,将得到的状态存储至记忆中
- 当记忆中存储的容量足够大时,随机从记忆中提取一定数量的状态转换,用状态转换中下一个状态来计算当前状态的目标价值
- 使用下面公式来计算目标价值与网络输出价值之间的均方差代价,使用小块梯度下降算法更新网络的参数。
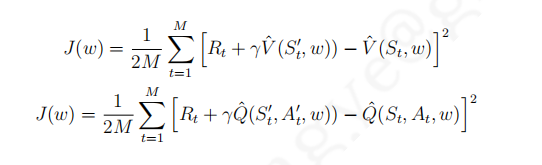 算法流程:
算法流程:
具体代码实现:
class DeepQNetwork:
def __init__(
self,
n_actions,
n_features,
learning_rate=0.01,
reward_decay=0.9,
e_greedy=0.9,
replace_target_iter=300,
memory_size=500,
batch_size=32,
e_greedy_increment=None,
output_graph=True,
):
self.n_actions = n_actions
self.n_features = n_features
self.lr = learning_rate
self.gamma = reward_decay
self.epsilon_max = e_greedy
self.replace_target_iter = replace_target_iter
self.memory_size = memory_size
self.batch_size = batch_size
self.epsilon_increment = e_greedy_increment
self.epsilon = 0 if e_greedy_increment is not None else self.epsilon_max
# 统计训练次数
self.learn_step_counter = 0
# 初始化记忆 memory [s, a, r, s_]
self.memory = np.zeros((self.memory_size, n_features * 2 + 2))
# 有两个网络组成 [target_net, evaluate_net]
self._build_net()
t_params = tf.get_collection('target_net_params')
e_params = tf.get_collection('eval_net_params')
self.replace_target_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)]
self.sess = tf.Session()
if output_graph:
# 开启tensorboard
# $ tensorboard --logdir=logs
# tf.train.SummaryWriter soon be deprecated, use following
tf.summary.FileWriter(r'D:\logs', self.sess.graph)
self.sess.run(tf.global_variables_initializer())
self.cost_his = []
def _build_net(self):
# -------------- 创建 eval 神经网络, 及时提升参数 --------------
self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s') # 用来接收 observation
self.q_target = tf.placeholder(tf.float32, [None, self.n_actions],
name='Q_target') # 用来接收 q_target 的值, 这个之后会通过计算得到
with tf.variable_scope('eval_net'):
# c_names(collections_names) 是在更新 target_net 参数时会用到
c_names, n_l1, w_initializer, b_initializer = \
['eval_net_params', tf.GraphKeys.GLOBAL_VARIABLES], 10, \
tf.random_normal_initializer(0., 0.3), tf.constant_initializer(0.1) # config of layers
# eval_net 的第一层. collections 是在更新 target_net 参数时会用到
with tf.variable_scope('l1'):
w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
l1 = tf.nn.relu(tf.matmul(self.s, w1) + b1)
# eval_net 的第二层. collections 是在更新 target_net 参数时会用到
with tf.variable_scope('l2'):
w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
self.q_eval = tf.matmul(l1, w2) + b2
with tf.variable_scope('loss'): # 求误差
self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval))
with tf.variable_scope('train'): # 梯度下降
self._train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)
# ---------------- 创建 target 神经网络, 提供 target Q ---------------------
self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_') # 接收下个 observation
with tf.variable_scope('target_net'):
# c_names(collections_names) 是在更新 target_net 参数时会用到
c_names = ['target_net_params', tf.GraphKeys.GLOBAL_VARIABLES]
# target_net 的第一层. collections 是在更新 target_net 参数时会用到
with tf.variable_scope('l1'):
w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
l1 = tf.nn.relu(tf.matmul(self.s_, w1) + b1)
# target_net 的第二层. collections 是在更新 target_net 参数时会用到
with tf.variable_scope('l2'):
w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
self.q_next = tf.matmul(l1, w2) + b2
def store_transition(self, s, a, r, s_):
# 判断是否包含对应属性 没有就赋予初值
if not hasattr(self, 'memory_counter'):
self.memory_counter = 0
# 纵向延伸
transition = np.hstack((s, [a, r], s_))
# 使用新的记忆替换掉旧网络的记忆
index = self.memory_counter % self.memory_size
self.memory[index, :] = transition
self.memory_counter += 1
def choose_action(self, observation):
# 给观测值加上batch_size维度
observation = observation[np.newaxis, :]
if np.random.uniform() < self.epsilon:
# forward feed the observation and get q value for every actions
actions_value = self.sess.run(self.q_eval, feed_dict={self.s: observation})
action = np.argmax(actions_value)
else:
action = np.random.randint(0, self.n_actions)
return action
def learn(self):
# 判断是否应该更新target-net网络了
if self.learn_step_counter % self.replace_target_iter == 0:
self.sess.run(self.replace_target_op)
print('\ntarget_params_replaced\n')
# 从以前的记忆中随机抽取一些记忆
if self.memory_counter > self.memory_size:
sample_index = np.random.choice(self.memory_size, size=self.batch_size)
else:
sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
batch_memory = self.memory[sample_index, :]
q_next, q_eval = self.sess.run(
[self.q_next, self.q_eval],
feed_dict={
self.s_: batch_memory[:, -self.n_features:], # fixed params
self.s: batch_memory[:, :self.n_features], # newest params
})
# change q_target w.r.t q_eval's action
q_target = q_eval.copy()
# 下面这几步十分重要. q_next, q_eval 包含所有 action 的值,
# 而我们需要的只是已经选择好的 action 的值, 其他的并不需要.
# 所以我们将其他的 action 值全变成 0, 将用到的 action 误差值 反向传递回去, 作为更新凭据.
# 这是我们最终要达到的样子, 比如 q_target - q_eval = [1, 0, 0] - [-1, 0, 0] = [2, 0, 0]
# q_eval = [-1, 0, 0] 表示这一个记忆中有我选用过 action 0, 而 action 0 带来的 Q(s, a0) = -1, 所以其他的 Q(s, a1) = Q(s, a2) = 0.
# q_target = [1, 0, 0] 表示这个记忆中的 r+gamma*maxQ(s_) = 1, 而且不管在 s_ 上我们取了哪个 action,
# 我们都需要对应上 q_eval 中的 action 位置, 所以就将 1 放在了 action 0 的位置.
# 下面也是为了达到上面说的目的, 不过为了更方面让程序运算, 达到目的的过程有点不同.
# 是将 q_eval 全部赋值给 q_target, 这时 q_target-q_eval 全为 0,
# 不过 我们再根据 batch_memory 当中的 action 这个 column 来给 q_target 中的对应的 memory-action 位置来修改赋值.
# 使新的赋值为 reward + gamma * maxQ(s_), 这样 q_target-q_eval 就可以变成我们所需的样子.
# 具体在下面还有一个举例说明.
batch_index = np.arange(self.batch_size, dtype=np.int32)
eval_act_index = batch_memory[:, self.n_features].astype(int)
reward = batch_memory[:, self.n_features + 1]
q_target[batch_index, eval_act_index] = reward + self.gamma * np.max(q_next, axis=1)
"""
假如在这个 batch 中, 我们有2个提取的记忆, 根据每个记忆可以生产3个 action 的值:
q_eval =
[[1, 2, 3],
[4, 5, 6]]
q_target = q_eval =
[[1, 2, 3],
[4, 5, 6]]
然后根据 memory 当中的具体 action 位置来修改 q_target 对应 action 上的值:
比如在:
记忆 0 的 q_target 计算值是 -1, 而且我用了 action 0;
记忆 1 的 q_target 计算值是 -2, 而且我用了 action 2:
q_target =
[[-1, 2, 3],
[4, 5, -2]]
所以 (q_target - q_eval) 就变成了:
[[(-1)-(1), 0, 0],
[0, 0, (-2)-(6)]]
最后我们将这个 (q_target - q_eval) 当成误差, 反向传递会神经网络.
所有为 0 的 action 值是当时没有选择的 action, 之前有选择的 action 才有不为0的值.
我们只反向传递之前选择的 action 的值,
"""
# 训练eval网络
_, self.cost = self.sess.run([self._train_op, self.loss],
feed_dict={self.s: batch_memory[:, :self.n_features],
self.q_target: q_target})
self.cost_his.append(self.cost)
# 因为在训练过程中会逐渐收敛所以此处动态设置增长epsilon
self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_max
self.learn_step_counter += 1
DDQN介绍
DQN算法在深度强化学习领域取得了不俗的成绩,不过其并不能保证一直收敛。
研究表明这种估计目标价值的算法过于乐观的高估了一些情况下的行为价值,导致算法会将次优行为价值一致认为最优行为价值,最终不能收敛到最佳价值函数。

编程-基于Pytorch实现DQN求解PuckWorld问题
PuckWorld环境介绍:
Puckworld(冰球世界),简单地说就是Agent去追逐世界中随机出现的目标物体。
- PuckWorld环境出现在《强化学习》第七讲中,它描述的是一个连续的二维空间中的个体追逐一个目标物体这样一个场景。
- 如下图所示:在矩形空间里,个体试图尽可能得靠近五角形的目标以获取更多的奖励;与此同时,目标物体(五角形)每隔一定的时间将重新出现的区域里随机的位置,个体需要对此做出反应,调整行为接近新位置下的目标物体。
-
- 该环境相比之前的格子世界环境最大的不同之处在于矩形区域是一个用二维连续变量描述的空间。此时要描述个体或目标物体的位置,必须要使用连续的值。
在经典的PuckWorld环境中,
个体的观测空间由6个变量组成,分别是:
- 2个变量描述个体的位置(水平和垂直方向上的坐标值)
- 2个变量描述目标物体的位置(水平和垂直方向上的坐标值)
- 个体运动的速度在水平和垂直方向上的分量。
个体的行为空间仍然是一维的离散空间,有5个可能的取值,分别为:
- 增加左、右、上、下四个方向的单位速率值
- 维持当前速度。环境的动力学体现在个体下一个时刻的位置由当前位置及其速度决定;目标物体以固定的周期随机刷新其位置;
实际实现效果:

绿色小球是我们的Agent,红色小球是我们的目标,他是会随机移动的。刚开始Agent并不理解这个陌生的环境,因此需要不断探索,在一次次完整序列之后,Agent逐渐理解,最后可以达到一看到目标,就会冲向他,并抓到目标获取最终胜利。
对Agent的颜色也进行了设置,离目标越远颜色越深,离目标越近颜色越浅。此外小球上的箭头表示当前Agent在状态上,执行动作的方向。
源码日后再上传