《面向快速图表示学习的自适应采样》2018-11-19
1.待解决的问题
??一种自适应分层采样方法来加速GCNs的训练。解决GNNs的不可扩展问题(计算卷积需要跨层递归扩展邻域,计算量大,占内存。传统的小批量训练无法提高卷积计算的速度,因为每批训练都会涉及大量的顶点,即使批处理的大小很小)
2.解决方法-采样
??大图训练是图神经网络应用的一大难点,因为“批量处理”的概念(batch)并不适用于图结构的数据,相互连接的节点和消息传递方式使得最终的计算图无法仅仅局限于想要预测的那部分节点。
??而采样是当前处理大图的主要方法:既然随机抽部分训练节点还不够,那就补上计算图所需要的其它节点,形成一个小的子图。对于对应的图卷积层来说,之后就在这个子图上做梯度下降。如果采样采得好,在小图学到的参数,在原来的大图上也适用。
采样的方式主要分为两类:Node-wise和Layer-wise。
??Node-wise是指从目标节点逐层地进行邻居采样,对每个节点都采固定数目的邻居节点。这种方式的好处是缓解了内存需求,但因为在计算同一层中各个节点的embedding时,大家用到的邻居相互之间是独立的,所以时间成本倾向于随着层数增加呈指数级别的上升,这样就不能采得很深。
??Layer-wise放弃从节点出发采样,而是在图卷积层的维度上,在每层采样固定数目的节点,这样对于采出来的子图,它的规模是可控的(不像邻居采样,采出来的子图可能很大)。
3.本文提出的快速训练方法
3.1模型
??采用自顶向下的方法逐层构造网络,以顶层为条件对底层进行采样。不同的父节点共享采样邻域。采用固定大小的采样,避免网络的过度扩展。
??该方法:层间信息共享,抽样节点的大小可控,分层抽样的采样器是自适应的。
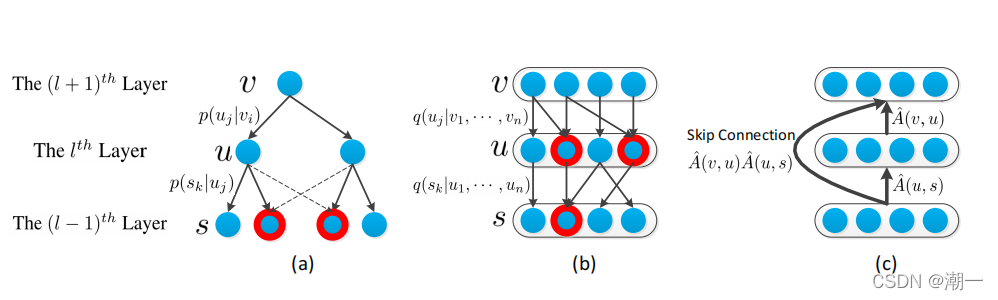
??不同的网络构建方法: the node-wise sampling approach; (b)
the layer-wise sampling method; ? the model considering the skip-connection.
??假设(a)和(b)中红色圆圈表示的节点在上层至少有两个父节点。
??因此,(a)中每个父节点的邻域不会被其他父节点扩展,邻域和其他父节点之间的连接是未使用的。相反,(b)中,所有的邻域都由父层中的节点共享,因此所有的层间连接都被利用。
??为了避免layer-wise sampling过度扩张问题,通过控制每一层采样邻域的大小来加速GCNs训练。自上而下逐层构建网络,根据上层的节点,对下层的节点进行有条件的抽样。
【有条件的采样的可实施性体现在以下两点:】
1.底层的节点是可见的,并且由上层的不同父节点共同使用(所有的层间连接都被利用)。因此可以重用采样的邻域信息。
2.由于下层节点是作为一个整体进行采样,因此很容易确定每一层的大小,避免邻域的过度扩张。
该方法的核心是为layer-wise sampling分层抽样定义一个适当的采样器。采样器的一个优化目标是使结果方差最小化。由于自顶向下采样和自底向上传播这两个过程,在网络中不一致。方差最小化是无法计算的。因此,使用一个自相关函数代替不可计算的部分来逼近最优采样器,然后在损失函数中加入方差。通过训练网络参数和采样器,可以显式地降低方差。
3.2与相关工作的对比
??最近,两种基于采样的方法,包括GraphSAGE[3]和FastGCN,被用于图的快速表示学习。
??GraphSAGE通过对每个节点的邻域进行采样计算节点表示,然后执行一个特定的聚合器进行信息融合。FastGCN模型将图的卷积解释为嵌入函数的积分变换,并独立地对每一层的节点进行采样。
??虽然我们的方法与这些方法密切相关,但我们在本文中开发了一种不同的抽样策略。
??与基于节点的GraphSAGE相比,我们的方法是基于分层抽样的,因为所有邻域都是一起抽样的,因此可以允许邻域共享。与FastGCN独立构建每一层不同的是,我们的模型能够捕获层间连接,因为下层的连接是在上层的连接上有条件地采样的。
3.3模型定义
??主要研究无向图。设G = (V, E)表示节点vi∈V,边(vi, vj)∈E的无向图,N表示节点个数。邻接矩阵A的每个元素Aij表示边(vi, vj)的权值。特征矩阵X的元素xi表示节点vi的d维特征。
??GCNs需要对每个节点前馈计算的邻域进行完全扩展。这使得在包含数十万个节点的大规模图上进行学习需要大量的计算和内存消耗。本文采用自适应采样的方法来加快前馈传播速度。该采样器适用于方差减小。
3.4模型步骤
??首先将GCN的前馈传播公式重新表述为“期望形式”。并相应引入de-wise抽样。然后,将节点抽样推广到layer-wise分层抽样。为了使产生的方差最小,通过显式地执行方差减少来学习出分层抽样器。最后,引入skip-connection跳跃连接的概念,并应用它来实现前馈传播的二阶近似【最接近原函数的抛物线,它比线性近似更为精确】。
3.4.1节点抽样 -> 分层抽样
优点:
1.采样只需要执行一次。
2. 所有抽样节点被当前层的所有节点共享,这个共享属性能够最大限度地增强消息传递。
3. 每一层的大小固定为n,采样节点总数仅随网络深度线性增长。
3.4.2显性方差减少构造抽样器
??通过减少采样过程引起的方差,因为高的方差可能会阻碍有效的训练。
??根据显性方差减的计算公式。是基于隐藏特征计算的,该特征在之前的层中被它的邻居聚合。
??然而,在自上而下采样框架下,除非网络完全由采样构建,否则底层的神经单元是未知的。
??为了这个问题,学习了每个节点的一个自依赖函数(基于节点特征)来确定其对采样的重要性。
为了实现方差减少,将方差加到损失函数中,并通过模型训练显式地最小化方差。通过考虑分类损失和方差,得到了混合损失L,为了最小化混合损耗,需要进行梯度计算。