原文链接:https://arxiv.org/pdf/2008.08294.pdf
Abstract
TNT分为3个stage:
- 预测agent未来的的target point
- 生成指向这些target point的trajectory
- 给这些trajectory打分,选出概率高的
这样遍可以做到一个多模态的预测(即直行,左转,右转,不同车道啥的)。
Introduction
TNT主要是为了解决agent的未来轨迹预测(支持多模态)。
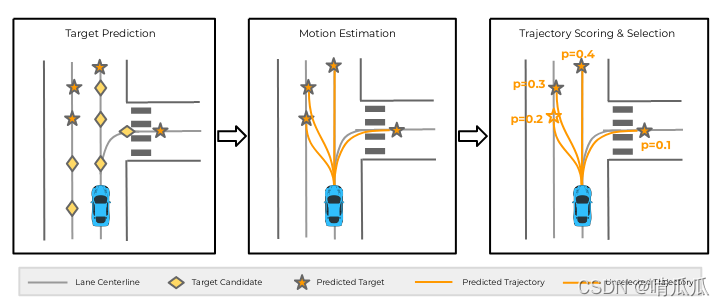
- target prediction:使用场景图预测了targets的分布
- target-conditioned motion estimation:预测了对于每一个target的时序序列
- scoring and selection:综合考虑所有轨迹后,评估了每一个轨迹的likelihood。选出概率高的轨迹输出。
Formulation
历史T帧的agent的states:
s
P
=
[
s
?
T
′
+
1
,
s
?
T
′
+
2
,
.
.
.
,
s
0
]
s_P=[s_{-T'+1}, s_{-T'+2},...,s_0]
sP?=[s?T′+1?,s?T′+2?,...,s0?]
未来T帧的agent的states:
s
F
=
[
s
1
,
s
2
,
.
.
.
,
s
T
]
s_F=[s_1,s_2,...,s_T]
sF?=[s1?,s2?,...,sT?]
历史T帧的环境变量(包括别的agents和场景元素):
c
P
=
[
c
?
T
′
+
1
,
c
?
T
′
+
2
,
.
.
.
,
c
0
]
c_P=[c_{-T'+1},c_{-T'+2},...,c_0]
cP?=[c?T′+1?,c?T′+2?,...,c0?]
我们用
x
=
(
s
P
,
c
P
)
x=(s_P,c_P)
x=(sP?,cP?)来表示历史的所有变量,那么给定历史后的未来预测的概率分布为
p
(
s
F
∣
x
)
p(s_F|x)
p(sF?∣x).
用
τ
(
c
P
)
\tau(c_P)
τ(cP?)表示根据
c
P
c_P
cP?获得的大概的target空间,则
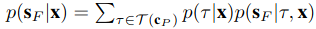
总的来看,第一步target prediction给出了
p
(
τ
∣
x
)
p(\tau|x)
p(τ∣x),即根据历史信息获得target。第二步target-conditioned motion estimation根据历史信息和target给出了未来的运动状态。整体符合条件概率的模型。最后一步scoring and selection就学习了打分的函数
?
(
s
F
)
\phi(s_F)
?(sF?),对预测的轨迹进行打分.
Target-driveN Trajectory Prediction
Overview:模型输入是encode过的场景,然后依次是,预测M个target,对每个target预测轨迹,打分后选取概率最高的K个轨迹。
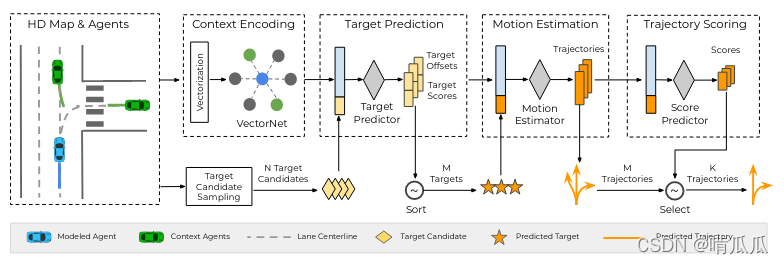
对于target和states,我们均使用二维物理坐标来表示
(
x
t
,
y
t
)
.
(x_t,y_t).
(xt?,yt?).
Scene context encoding
如果有高精地图的话,使用VectorNet来encode,其中使用polyline表示lanes,agent的trajectory,可作为
c
P
c_P
cP?和
s
P
s_P
sP?. 最后输出的是对于每个agent的feature
x
x
x.
如果没有高精地图,使用ConvNet来编码也可以。
Target prediction
假设有N个target。对于这N个target,我们都要预测一个offset。
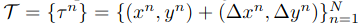
整个target的分布为:
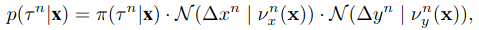
其中
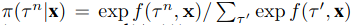
类似于softmax中的算法,f获得的是所有target中的任意一个的分数,为了获得每一个target在所有target中的概率,计算了
π
\pi
π.
N ( . ∣ v ( . ) ) N(.|v(.)) N(.∣v(.))是一个正态分布,v是平均值,unit variance。即给定平均值和单位方差,offset的一个正态分布。其中这个和mean的distance采用的是Huber(靠近0的二次函数,远的一次函数)。
这里面的f和v都是可学的,经过2层MLP的结果。输入都是大概的目标点 ( x k , y k ) (x^k,y^k) (xk,yk)和场景的feature x x x.
Loss计算如下
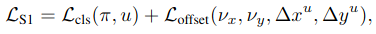
其中分为不同target的cross entropy loss和offset的Huber loss。
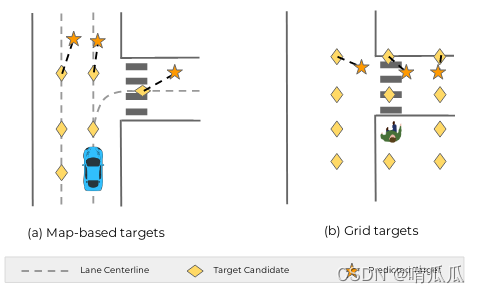
对于car来说,target candidate是从lane上等间隔地sample的。对于pedestrian,则是用网格取点。对应图中的菱形。
然后预测的是
(
π
,
Δ
x
,
Δ
y
)
(\pi, \Delta x,\Delta y)
(π,Δx,Δy),即每个target的概率和offset。对应图中的五角星。
实际中,本文采用了非常大的target candidate池子,N=1000,经过模型后从当中选择了M=50个最高概率的结果。
Target-conditioned motion estimation
这一步要预测未来的states。这个未来的states的likelihood可以表示为
p
(
s
F
∣
τ
,
x
)
=
Π
t
=
1
T
(
p
(
s
t
∣
τ
,
x
)
)
p(s_F|\tau,x)=\Pi_{t=1}^T(p(s_t|\tau,x))
p(sF?∣τ,x)=Πt=1T?(p(st?∣τ,x))
这个公式的成立依赖于两条假设
- 每一个time step都是独立的,这可以大幅提升运算的速度。有很多论文都这么做。
- 给定target后的预测是单模态的。这个是因为我们的预测在一个比较短的时间T内。
使用两层MLP,把场景feature
x
x
x和target
τ
\tau
τ作为输入,输出一个概率最高的未来轨迹
[
s
^
1
,
.
.
.
,
s
^
T
]
[\hat{s}_1,...,\hat{s}_T]
[s^1?,...,s^T?].此处采取了teacher forcing的技巧(在RNN中,一般训练方法是把上一步输出的state作为下一步的输入,以此类推。而teacher forcing则是每次输入的是ground truth)。训练的时候每一个输入的target采用的是ground truth而非上一步得出的结果。
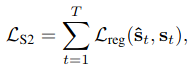
Loss是每一个时刻的ground truth和预测结果的距离(Huber loss)之和。
Trajectory scoring and selection
这一步是对于一整条预测的轨迹进行打分。当中
g
(
.
)
g(.)
g(.)是一个2层的MLP。
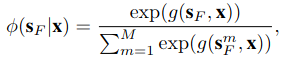
Loss的计算采取对预测分数和ground truth分数的交叉熵。
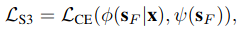
每一个预测的轨迹的ground truth的分数是它和ground truth的距离来计算的。
ψ
(
s
F
)
=
e
x
p
(
?
D
(
s
,
s
G
T
)
/
α
)
∑
s
′
e
x
p
(
?
D
(
s
′
,
S
G
T
)
/
α
)
\psi(s_F)=\frac{exp(-D(s,s_{GT})/\alpha)}{\sum_{s'}exp(-D(s',S_{GT})/\alpha)}
ψ(sF?)=∑s′?exp(?D(s′,SGT?)/α)exp(?D(s,sGT?)/α)?
直觉上的话就是对于多个模态的预测结果,分别计算每一条和gt(gt只有一个模态)的距离,用这些距离算概率(类似softmax的方法)。其中距离的计算是两条轨迹上同时刻点点间的最大距离。
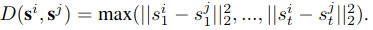
为了避免太过接近的输出,采用NMS类似的做法。先根据分数排序,从高到低放入选中的轨迹,如果太接近已经选出来的轨迹。
Training and inference details
这是一个端端训练的模型,loss就是上述loss的和。
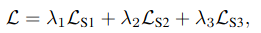
在inference中的步骤为:
- 场景encode
- 根据地图找出N个target candidate作为输入,从中用 π ( τ ∣ x ) \pi(\tau|x) π(τ∣x)选出概率最高的M个target
- 预测这M个target的轨迹,获得 p ( s F ∣ τ , x ) p(s_F|\tau,x) p(sF?∣τ,x)
- 对这M个轨迹打分 ? ( s F ∣ τ , x ) \phi(s_F|\tau,x) ?(sF?∣τ,x),选出概率高的K个轨迹
Metrics
Average Displacement Error (ADE):轨迹上每个点和gt的每个点的距离的平均
Final Displacement Error (FDE):target的距离
Miss rate (MR):所有target距离gt的target差2m以上的比例