[人工智能]吴恩达机器学习作业4：神经网络(反向传播)（Python实现）

机器学习练习 4 - 神经网路

Introduction

在本练习中，将实现神经网络的反向传播算法，并将其应用于手写数字识别任务。我们将通过反向传播算法实现神经网络成本函数和梯度计算的非正则化和正则化版本，还将实现随机权重初始化和使用网络进行预测的方法。

1 Neural Networks

在前面的练习中，实现了神经网络的前馈传播，并使用它以及我们提供的权重来预测手写数字。在本练习中，您将实现反向传播算法来学习神经网络的参数。

1.1 Visualizing the data

编写代码加载数据，并通过调用函数显示数据。

先导入相关的函数库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat

编写加载数据的代码，并且传入参数：数据文件的路径

def load_data(path):
    data=loadmat(path)
    X=data['X']
    y=data['y'].flatten()
    return X,y

随机绘制100个数字

def plot_images_100(X):
    ind=np.random.choice(range(5000),100)
    images=X[ind]
    fix,ax_array=plt.subplots(10,10,sharex=True,sharey=True,figsize=(8,8)) #绘制的图形为：10*10，并且公用x和y
    for r in range(10):
        for c in range(10):
            ax_array[r,c].matshow(images[r*10+c].reshape(20,20),cmap='gray_r')#每一个图形都是400个数字构成，所以要reshape为 20*20
    plt.xticks([])
    plt.yticks([])
    plt.show()

X,y=load_data('ex4data1.mat')

查看X和y的数据规模以及具体数据

X,y

(array([[0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.],
        ...,
        [0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.]]),
 array([10, 10, 10, ...,  9,  9,  9], dtype=uint8))

调用plot_images_100函数，查看绘制的图形

这与上一个练习中使用的数据集相同。在ex4data1.mat中有5000个训练示例，其中每个训练示例是一个 $20?20$ 像素的数字灰度图像。每个像素用一个浮点数表示，表示该位置的灰度强度。$20?20$ 的像素网格被"展开"成一个400维的向量。每个训练示例在数据矩阵X中都变成了一行。这就给了一个 $5000?400$ 的矩阵X，其中每一行都是一个手写数字图像的训练示例。

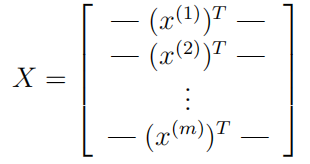
训练集的第二部分是一个5000维的向量y。将数字0映射到值10。因此，一个"0"数字被标记为"10"，而数字"1"到"9"按其自然顺序被标记为"1"到"9"。

plot_images_100(X)

?

?

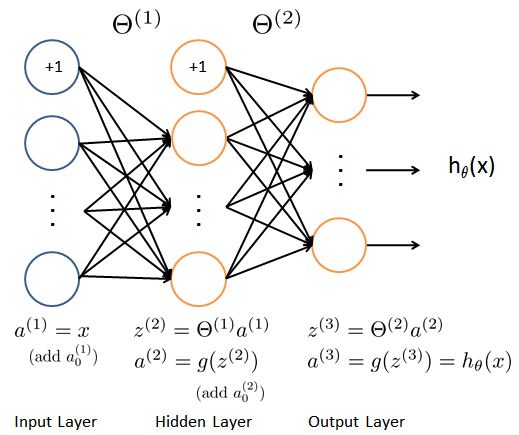
1.2 Model representation

神经网络如图所示:它有$3$个层，一个输入层，一个隐藏层和一个输出层。

1.2.1 读取数据

获取训练数据集,并且进行相应的处理

raw_X,raw_y=load_data('ex4data1.mat')
X=np.insert(raw_X,0,np.ones(raw_X.shape[0]),axis=1)#在第0列插入全1
X.shape

(5000, 401)

将标签值$(1,2,3,4,...,10)$转化成非线性相关的向量，即$y$向量对应位置为$1$，比如$y[5]=1$那么$y[5]=[0,0,0,0,1,0,0,0,0,0]$。

def expand_y(y):
    result=[]
    #将整数y[i]修改为向量，对应下标位置置为1，其余为0
    for it in y:
        y_array=np.zeros(10)
        y_array[it-1]=1
        result.append(y_array)
    return np.array(result)

y=expand_y(raw_y)
y.shape

(5000, 10)

1.2.2 读取权重

由于图像的大小是$20\times 20$，即400个输入层单位（不包括总是输出+1的额外偏置单位）。您已经得到了一组已经训练过的网络参数(${\theta }^{(1)},{\theta }^{(2)}$)。这些存储在$ex4weights.mat$中，编写代码得到$\theta 1$和$\theta 2$。$\theta 1$的规模为$25?401$，$\theta 2$的规模为$10?26$。

def load_weight(path):
    data=loadmat(path)
    return data['Theta1'],data['Theta2']

t1,t2=load_weight('ex4weights.mat')
t1.shape,t2.shape

((25, 401), (10, 26))

1.2.3 参数展开

def serialize(t1,t2):
    #参数展开
    return np.r_[t1.flatten(),t2.flatten()]

theta=serialize(t1, t2) #扁平化参数
theta.shape

(10285,)

1.2.4 提取参数

def deserialize(seq):
    #提取参数
    return seq[:25*401].reshape(25,401),seq[25*401:].reshape(10,26)

1.3 Feedforward and cost function

现在将实现神经网络的成本函数和梯度。神经网络的代价函数（没有正则化）是：

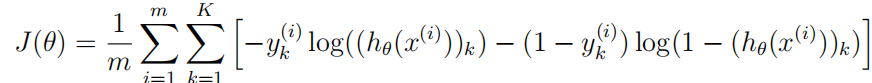
$k=10$是可能的标签的总数。