本篇文章是根据视频(?link.)所作的学习笔记,旨在对机器学习的相关知识更好的理解和巩固。本人基础较弱,推导中看不懂的公式可能会细究,如果有理解不当之处也欢迎指出。
本篇主要介绍线性分类中的软分类模型(硬分类模型见上篇),用概率的方法进行分类。包括概率判别模型中的逻辑回归,概率生成模型中的GDA和朴素贝叶斯。
概率判别模型:根据样本数据学习出一个模型,然后对待分类数据进行概率计算,结果与0.5进行比较即可分类。
概率生成模型:根据两类样本数据学习出两个模型,然后将待分类数据带入到两个模型中,比较结果的大小进行分类。
·?数据介绍
,且y=1时记为C1类,对应样本数量为N1;y=0时记为C2类,对应样本数量为N2。
概率判别模型之逻辑回归(Logistic Regression)
逻辑回归模型主要是通过一个sigmoid激活函数来实现线性分类的。
sigmoid函数:
分析该函数:,图像如下:

软分类得到的是一个[0,1]的概率值p(y|x)。得到该表达式之前,先介绍一下数据属于C1,C2类的概率表达:
构造,这个构造还是很巧妙的,Y=1时,刚好是P1;Y=0时,刚好是P0;P0+P1=1,由于sigmoid函数以1/2为划分,所以当P(Y|X)结果大于0.5时则为C1类,否则为C2类。
求参数:
记
则??
末尾的红色部分加上负号也叫做二分类问题中的交叉熵损失函数(cross entropy):
逻辑回归的推导到这里就戛然而止啦!精彩在后面~
概率生成模型之GDA
由之前的学习我们知道:
先假设先验数据服从伯努利分布,
则先验概率
并假设,同方差,不同均值
则似然概率
有了先验概率和似然概率,可得出目标函数表达式:
为了方便下面的推导,把[]内部的三项分分别记为J1,J2,J3,即:
,
,
其中,,
,一个一个来求:
1)求参数
,只与J3有关。
对应的是Y=1 时的概率,所以分子为N1;Y=0时的先验概率对应1-
=N2/N
2)求参数
,与J1,J2项有关,形式相同,求出一个,另一个同理。
两边同时乘以
,得??
,同理,
3)求参数
,与J1+J2有关,先看?
的化简结果,再带入J1,J2
其中,
为一实数,实数与自身的迹tr()相同
引入一个迹的性质:tr(AB)=tr(BA),里面的元素满足交换律
注意了,里面?
这一项跟方差S有点像,等于NS
此时,就可以得出J1+J2的表达式了
这里加入一些求导的性质:行列式求导
,迹的求导
终于推导完啦!撒花!!!这个也太长了。。。
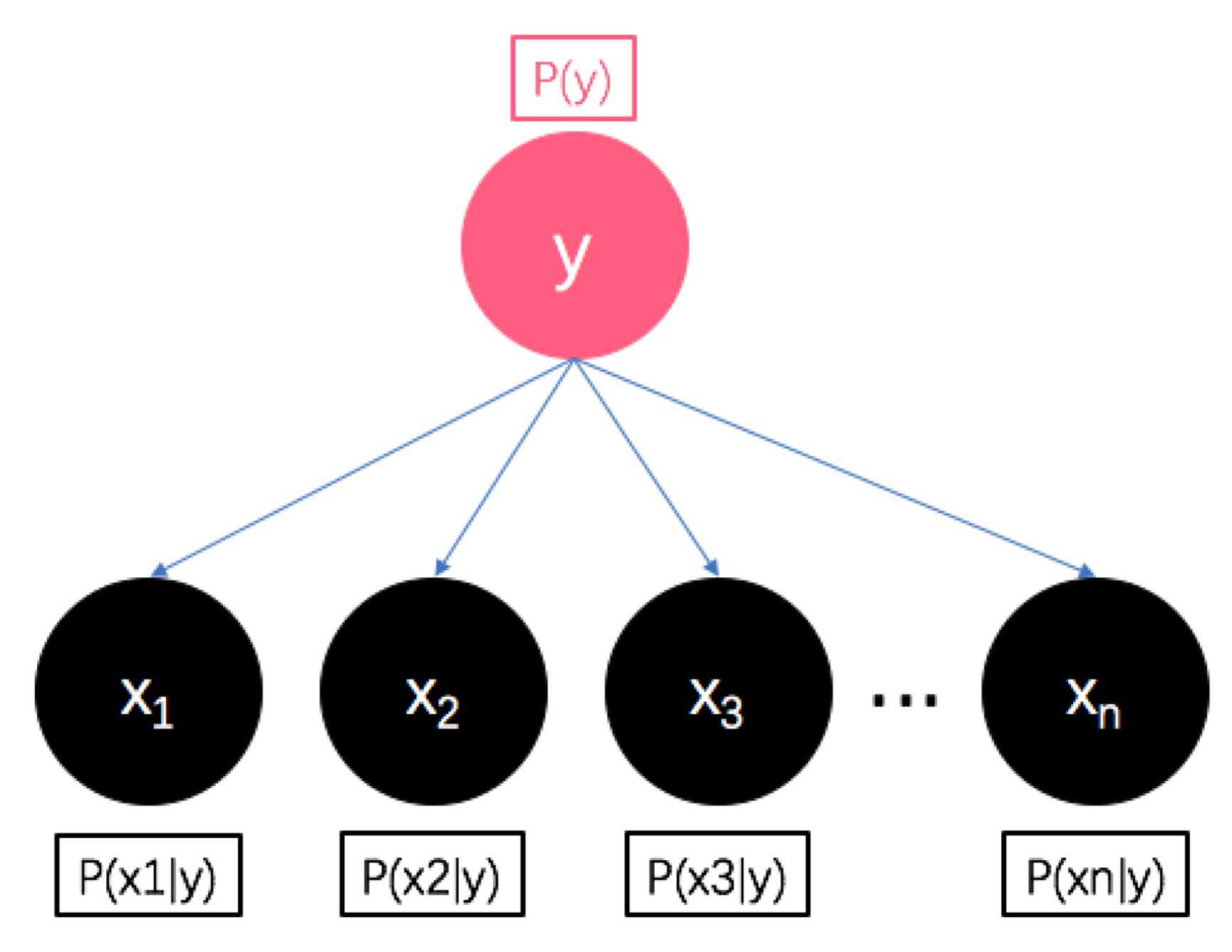
概率生成模型之朴素贝叶斯
up主说这个是最简单的,“朴素”可不就约等于简单嘛
之所以朴素是因为作了一个条件独立性假设,即每个数据的特征(属性)之间都是相互独立的,直接连乘就可以啦。?
咱就是说今天下班啦!吃年夜饭去啦!各位新年快乐,虎年如虎~