[人工智能]星形线再回顾--切线（点）构成曲线

在之前的星形线探索中，

【深度学习导数回顾】滑竿问题--导数求极值--星形线

【深度学习导数回顾】滑竿问题--导数求极值--星形线_aaajj的专栏-CSDN博客

我们了解到，星形线的方程可以描述为参数方程，

?y=(cost)^3

?x=(sint)^3

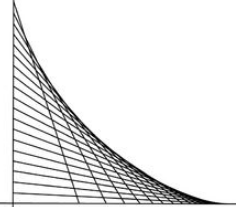
这里，星形线可以看成是滑竿滑过面积的边界，滑竿（直线）是星形线的切线么？

我们从曲线方程来进行反推。

星形线上一点p，其切线为 y = ax + b

其中 a为斜率，

即a = dy/dx = (dy/dt) / (dx/dt)

= (3(cost)^2 * -sint) / (3(sint)^2 * cost) = -cost / sint

再带入

y=(cost)^3

?x=(sint)^3

得到 b= cost

切线y = ax + b 和 y轴的交点Y0 = b = cost

切线y = ax + b 和 x轴的交点 X0 = -b/a = sint

X0 ^ 2 + Y0^2 = 1

可以看出，切线就是滑竿，切线和坐标轴的相交线段长度不变。

这个很有意思。

公交车对开的门，滑出了星形线轨迹