[人工智能]文本表达：从BERT-flow到BERT-whitening、SimCSE

文本表达：从BERT-flow到BERT-whitening、SimCSE

Sentence Embeddings：即能表征句子语义的特征向量，获取这种特征向量的方法有无监督和有监督两种，在无监督学习中，我们首先会考虑利用预训练好的大型预训练模型获取[CLS]或对句子序列纬度做MeanPooling来得到一个输入句子的特征向量。在笔者之前的文章中就利用这一方法获取论文中所有句子的特征向量后传入DGCNN来抽取摘要。

但这种方法被证明了有一个致命的缺点即： Anisotropy(各向异性) ，通俗来说就是在我们熟悉的预训练模型训练过程中会导致word embeddings的各维度的特征表示不一致。导致我们获取的句子级别的特征向量也无法进行直接比较。

目前比较流行解决这一问题的方法有

• 1、线性变换(在本文的第一二点中会详细介绍）：bert-flow 或 bert-whitening，无论是在bert中增加flow层还是对得到句子向量矩阵进行白化其本质都是通过一个线性变换来缓解Anisotropy。
• 2、对比学习：先对句子进行传统的文本增广，如转译、删除、插入、调换顺序等等，再将一个句子通过两次增广得到的新句子作为正样本对，取其他句子的增广作为负样本，进行对比学习，模型的目标也很简单，即拉近正样本对的embeddings，同时增加与负样本的距离。
• 3、SimCSE: Simple Contrastive Learning of Sentence Embeddings，发现利用预训练模型中自带的Dropout mask作为“增广手段”得到的Sentence Embeddings，其质量远好于传统的增管方法，其无监督和有监督方法无监督语义上达到SOTA。

1、BERT-flow

BERT表示存在的问题

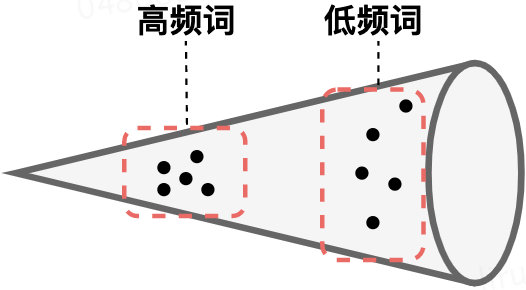
1. BERT的词向量在空间中不是均匀分布，而是呈锥形。作者发现高频词都靠近原点（所有的均值），而低频词远离原点，相当于这两种词处于了空间中不同的区域，那高频词和低频词之间的相似度就不再适用了
2. 低频词的分布很稀疏。低频词表示得到的训练不充分，分布稀疏，导致该区域存在语义定义不完整的地方（poorly defined），这样算出来的相似度也有问题。

BERT-flow

基于以上对相似度的深入探讨和问题研究，，作者采用一个变换，将 BERT encode 的句子表达转换到一个各向同性且分布较均匀的空间。而标准的高斯分布刚好是一个各向同性的空间，且是一个凸函数，语义分布也更平滑均匀。即BERT-flow基于流式生成模型，将BERT的表示可逆地映射到一个均匀的空间，上述的问题就迎刃而解了：

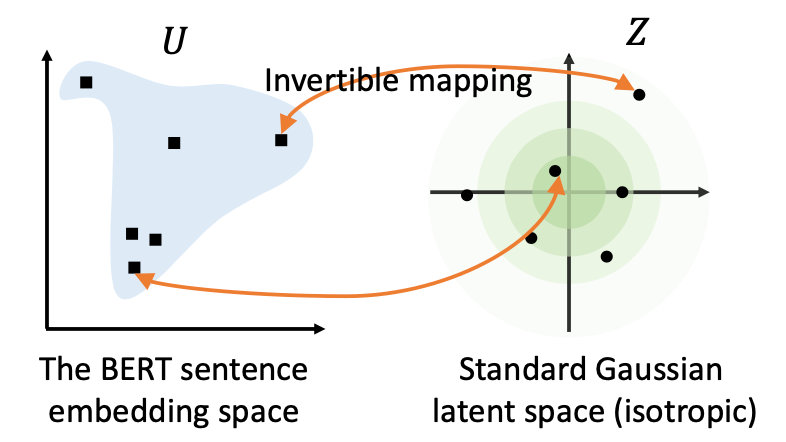
于是，变换就来了。BERT-flow 采用一种流式可逆变换，记为：

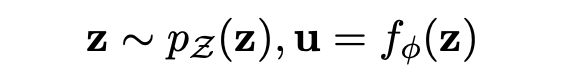
其中 u 就是 BERT 空间向量（observe space），z 即是高斯空间向量（latent space）， 则是一个可逆变换，这个变换也是模型需要学出来的。

根据变元定理，观测空间的 u 的概率密度函数为：

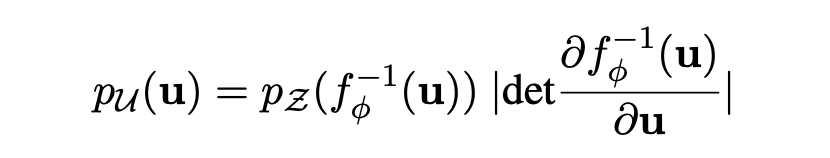
那模型优化目标的也就是最大化这个 u 的边际概率。

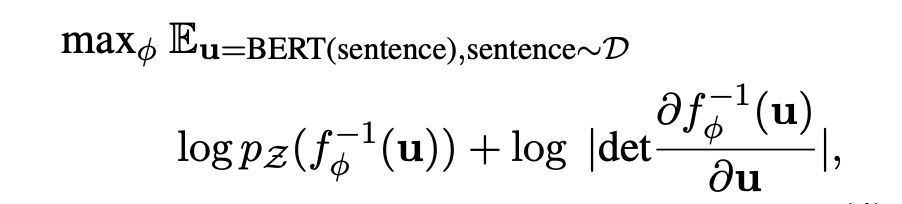
最后，通过无监督的方式 maximize 这个优化目标，得到可逆的映射变换 f，这其实就是在 Bert pre-train model 后接了一个 flow 变换的模型，让其继续 pre-train，学出 flow 变换，从而完成向量空间的 transform。

2、BERT-whitening

首先我们想一想文本相似度计算的方法，是不是先将文本表示为向量，然后计算两个句向量之间的余弦相似度，通过相似度的大小判断这两个文本是否相似。

那么这里就出现了一个问题：余弦相似度为什么就能够计算两个向量的相似性呢？想弄清楚这个问题，就需要我们对于向量的内积有一个充分的理解。

向量的内积

在线性代数中，我们知道，对于向量$A$和$B$来说，它们的内积形式是这样的

从上面的公式我们可以看出，向量内积的运算是将两个向量映射为实数。接下来，我们从几何的角度来进行分析，假设 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZJfmpIqb-1643617651125)(https://www.zhihu.com/equation?tex=A)] 和 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oRMHKR7c-1643617651126)(https://www.zhihu.com/equation?tex=B)] 为二维向量来进行分析，则：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TOQ3DnSY-1643617651126)(https://www.zhihu.com/equation?tex=A+%5Ccdot+B%3D%7CA%7C%7CB%7Ccos%28%5Calpha%29%5Ctag%7B2%7D)]

经过变换后我们就可以得到

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-I1pvIbCc-1643617651126)(https://www.zhihu.com/equation?tex=cos%28%5Calpha%29%3D+%5Cfrac+%7BA+%5Ccdot+B%7D+%7B%7CA%7C%7CB%7C%7D%5Ctag%7B3%7D)]

其几何图为：

可以看到，向量 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5bXl9p6w-1643617651127)(https://www.zhihu.com/equation?tex=A)] 与 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rzvKiM4U-1643617651127)(https://www.zhihu.com/equation?tex=B)] 的乘积为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ndn4XrDc-1643617651127)(https://www.zhihu.com/equation?tex=A)] 到 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AV9kUJqd-1643617651128)(https://www.zhihu.com/equation?tex=B)] 投影的长度乘以 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BF3Mjfub-1643617651128)(https://www.zhihu.com/equation?tex=B)] 的模。 假设 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uN55LOoM-1643617651128)(https://www.zhihu.com/equation?tex=%7CB%7C%3D1)] ，则公式变为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PBd8CoiB-1643617651128)(https://www.zhihu.com/equation?tex=A+%5Ccdot+B%3D%7CA%7Ccos%28%5Calpha%29+%5Ctag%7B4%7D)]

也就是说，*向量* [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JJPFehf5-1643617651129)(https://www.zhihu.com/equation?tex=A)] *与* [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0OMyDsKy-1643617651129)(https://www.zhihu.com/equation?tex=B)] *的乘积可以看作* [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1R4gPfvW-1643617651129)(https://www.zhihu.com/equation?tex=A)] *向* [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ndcSaE8z-1643617651129)(https://www.zhihu.com/equation?tex=B)] *所在直线投影的标量大小*。

我们把 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-le2qI05P-1643617651130)(https://www.zhihu.com/equation?tex=A)] 和 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DxNwHxAM-1643617651130)(https://www.zhihu.com/equation?tex=B)] 这两个向量扩展至 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XYUML71v-1643617651130)(https://www.zhihu.com/equation?tex=d)] 维，可以得到

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AYXvEGov-1643617651130)(https://www.zhihu.com/equation?tex=cos%28A%2CB%29%3D+%5Cfrac+%7B%5Csum_%7Bi%3D1%7D%5E%7Bd%7Da_%7Bi%7Db_%7Bi%7D%7D+%7B%5Csqrt+%7B%5Csum_%7Bi%3D1%7D%5E%7Bd%7Da_%7Bi%7D%5E2%7D+%5Csqrt+%7B%5Csum_%7Bi%3D1%7D%5E%7Bd%7Db_%7Bi%7D%5E2%7D%7D%5Ctag%7B4%7D+)]

向量的模的计算公式为： [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VvGL26CJ-1643617651131)(https://www.zhihu.com/equation?tex=%7CA%7C%3D%5Csqrt+%7Ba_%7B1%7D%5E2%2Ba_%7B2%7D%5E2%2B…%2Ba_%7Bn%7D%5E2%7D)]

公式(4)也被我们称为欧式距离。然而，别忘了一件事情，上述等号只在“标准正交基”下成立。换句话说，向量的“夹角余弦”本身是具有鲜明的几何意义的，但上式右端只是坐标的运算，坐标依赖于所选取的坐标基，基底不同，内积对应的坐标公式就不一样，从而余弦值的坐标公式也不一样。

标准正交基

我们知道，对于两个向量 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fV8nDraP-1643617651131)(https://www.zhihu.com/equation?tex=A)] 和 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JRRUZt1x-1643617651131)(https://www.zhihu.com/equation?tex=B)] 来说，如果

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vzmKoVep-1643617651131)(https://www.zhihu.com/equation?tex=A+%5Ccdot+B+%3D+0%5Ctag%7B5%7D)]

那么，我们称这两个向量正交(零向量与任何向量正交)。 我们知道，在n维的欧式空间中，由n个向量组成的正交向量组称为正交基；由单位向量组成的正交基称为标准正交基。

对于一个向量$A$来说，其中不同维度的值表示的就是在该维上的投影，是一个标量。所以，我们可以大致的得出一个结论：要准确描述向量，首先要确定一组基，然后给出在基所在的各个维度上的投影值，就可以了。

为了方便求坐标，我们希望这组基向量模长为 1。因为向量的内积运算，当模长为 1 时，内积可以直接表示投影。然后还需要这组基是线性无关的，我们一般用正交基，非正交的基也是可以的，不过正交基有较好的性质。

到这里是不是就明白了，Bert模型输出的 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qLipDcyn-1643617651132)(https://www.zhihu.com/equation?tex=%5BCLS%5D)] 向量为什么在文本语义计算任务中无法取得好的效果呢，那么原因可能就是此时的句向量所属的坐标系并非标准正交基。

而且如果基的数量少于向量本身的维数，则可以达到降维的效果。但是我们还没回答一个最关键的问题：如何选择基才是最优的。或者说，如果我们有一组 N 维向量，现在要将其降到 K 维（K 小于 N），那么我们应该如何选择 K 个基才能最大程度保留原有的信息？

一种直观的看法是：希望投影后的投影值尽可能分散，因为如果重叠就会有样本消失。当然这个也可以从熵的角度进行理解，熵越大所含信息越多。

所以，这里我们希望的是投影后的数值尽可能的分散，那么，该如何让投影值分散呢？而在数学中，可以用方差来表示数值的分散程度。

方差与协方差

我们知道在一维的情况下，方差的计算如下

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Kf6PhKlr-1643617651132)(https://www.zhihu.com/equation?tex=Var%28a%29%3D+%5Cfrac+1+%7Bm%7D+%5Csum_%7Bi%3D1%7D%5E%7Bm%7D%28a_%7Bi%7D-+%5Cmu%29%5E2%5Ctag%7B6%7D)]

在多维的情况下，我们使用的协方差，计算如下

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AKaPjpOP-1643617651132)(https://www.zhihu.com/equation?tex=Cov%28a%2Cb%29%3D+%5Cfrac+%7B1%7D+%7Bm-1%7D+%5Csum_%7Bi%3D1%7D%5E%7Bm%7D%28a_%7Bi%7D-+%5Cmu_%7Ba%7D%29%28b_%7Bi%7D-+%5Cmu_%7Bb%7D%29%5Ctag%7B7%7D+)]

这里为了方便计算，我们把均值 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KTEw8sC0-1643617651132)(https://www.zhihu.com/equation?tex=%5Cmu_%7Ba%7D)] 和 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aUzjZV4h-1643617651133)(https://www.zhihu.com/equation?tex=%5Cmu_%7Bb%7D)] 置为0，当样本数较大时，不必在意其是 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dJGrzmhk-1643617651133)(https://www.zhihu.com/equation?tex=m)] 还是 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OaRl2Up3-1643617651133)(https://www.zhihu.com/equation?tex=m-1)] ，这里为了方便统一取 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6loPa2Y3-1643617651133)(https://www.zhihu.com/equation?tex=m)] ，可得
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ypr4QYYn-1643617651134)(https://www.zhihu.com/equation?tex=Cov%28a%2Cb%29%3D+%5Cfrac+%7B1%7D+%7Bm%7D+%5Csum_%7Bi%3D1%7D%5E%7Bm%7Da_%7Bi%7Db_%7Bi%7D%5Ctag%7B8%7D)]

当协方差为 0 时，表示两个变量完全线性不相关。为了让协方差为 0，我们选择第二个基时只能在与第一个基正交的方向上进行选择，因此最终选择的两个方向一定是正交的。

到这里，我们就可以得到一个优化目标：*将一组 N 维向量降为 K 维，其目标是选择 K 个单位正交基，使得原始数据变换到这组基上后，各变量两两间协方差为 0，而变量方差则尽可能大（在正交的约束下，取最大的 K 个方差）。*

对于向量 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qFNYmYZp-1643617651134)(https://www.zhihu.com/equation?tex=A)] 和 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DYkn7wpo-1643617651134)(https://www.zhihu.com/equation?tex=B)] 来说，我们按照行组成一个向量矩阵 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jAHsyfzi-1643617651134)(https://www.zhihu.com/equation?tex=X)] 为

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RIFgzdci-1643617651135)(https://www.zhihu.com/equation?tex=X+%3D%5Cbegin%7Bpmatrix%7D++a_%7B1%7D%26+%26a_%7B2%7D+%26…%26a_%7Bn%7D+%5C%5C+++b_%7B1%7D%26+%26b_%7B2%7D+%26…%26b_%7Bn%7D++%5Cend%7Bpmatrix%7D%5Ctag%7B9%7D)]

然后根据协方差的计算公式，可得

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-T19lmKCc-1643617651135)(https://www.zhihu.com/equation?tex=%5Cfrac+%7B1%7D%7Bm%7D+XX%5ET%3D%5Cbegin%7Bpmatrix%7D+%5Cfrac+%7B1%7D%7Bm%7D+%5Csum_%7Bi%3D1%7D%5E%7Bm%7Da_%7Bi%7D%5E2+%26+%5Cfrac+%7B1%7D%7Bm%7D+%5Csum_%7Bi%3D1%7D%5E%7Bm%7Da_%7Bi%7Db_%7Bi%7D+%5C%5C++%5Cfrac+%7B1%7D%7Bm%7D+%5Csum_%7Bi%3D1%7D%5E%7Bm%7Da_%7Bi%7Db_%7Bi%7D+%26+%5Cfrac+%7B1%7D%7Bm%7D+%5Csum_%7Bi%3D1%7D%5E%7Bm%7Db_%7Bi%7D%5E2+%5Cend%7Bpmatrix%7D%3D%5Cbegin%7Bpmatrix%7DCov%28a%2Ca%29+%26+Cov%28a%2Cb%29+%5C%5C+Cov%28b%2Ca%29+%26+Cov%28b%2Cb%29+%5Cend%7Bpmatrix%7D%5Ctag%7B10%7D)]

我们可以看到这个矩阵对角线上的分别是两个变量的方差，而其它元素是 a 和 b 的协方差。两者被统一到了一个矩阵里。 我们很容易被推广到一般情况：

设我们有 m 个 n 维数据记录，将其排列成矩阵 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LDnqZWGr-1643617651135)(https://www.zhihu.com/equation?tex=X_%7Bn%2Cm%7D)] ，设 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OgqfLAKP-1643617651136)(https://www.zhihu.com/equation?tex=%5Cfrac+%7B1%7D%7Bm%7DXX%5ET)] ，则 C 是一个对称矩阵，其对角线分别对应各个变量的方差，而第 i 行 j 列和 j 行 i 列元素相同，表示 i 和 j 两个变量的协方差。

由此可知，我们需要将除对角线外的其它元素化为 0，并且在对角线上将元素按大小从上到下排列（变量方差尽可能大），这里就是将协方差转为一个单位矩阵，也就是矩阵的对角化。

设原始数据矩阵 X 对应的协方差矩阵为 C，而 P 是一组基按行组成的矩阵，设 Y=PX，则 Y 为 X 对 P 做基变换后的数据。设 Y 的协方差矩阵为 D，我们推导一下 D 与 C 的关系：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lajmzwIP-1643617651136)(https://www.zhihu.com/equation?tex=D%3D%5Cfrac+%7B1%7D%7Bm%7DYY%5ET%3D%5Cfrac+%7B1%7D%7Bm%7D%28PX%29%28PX%29%5ET%5C%5C%3D%5Cfrac+%7B1%7D%7Bm%7DPXP%5ETX%5ET%3DP%28%5Cfrac+%7B1%7D%7Bm%7DXX%5ET%29P%5ET%5C%5C%3DPCP%5ET%5Ctag%7B11%7D+)]

这样我们就看清楚了，我们要找的 P 是能让原始协方差矩阵对角化的 P。换句话说，优化目标变成了寻找一个矩阵 P，满足 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sbka1fPe-1643617651139)(https://www.zhihu.com/equation?tex=PCP%5ET)] 是一个对角矩阵，并且对角元素按从大到小依次排列，那么 P 的前 K 行就是要寻找的基，用 P 的前 K 行组成的矩阵乘以 X 就使得 X 从 N 维降到了 K 维并满足上述优化条件。

whitening

回到Bert本身的输出，根据上述的协方差矩阵，作者假设有一组句子向量，也可以写为行向量 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TV7EB9Qm-1643617651139)(https://www.zhihu.com/equation?tex=%5Cleft+%5C%7Bx%5Cright+%5C%7D_%7Bi%3D1%7D%5EN)] ，然后对 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QJlExzsR-1643617651140)(https://www.zhihu.com/equation?tex=%5Cleft+%5C%7Bx%5Cright+%5C%7D_%7Bi%3D1%7D%5EN)] 进行如下线性变换

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TY2FlZpf-1643617651140)(https://www.zhihu.com/equation?tex=%5Cwidetilde%7Bx%7D_%7Bi%7D%3D%28x_%7Bi%7D-%5Cmu%29W%5Ctag%7B12%7D+)]

使得 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hApNo0zB-1643617651140)(https://www.zhihu.com/equation?tex=%5Cleft+%5C%7B%5Cwidetilde%7Bx%7D_%7Bi%7D%5Cright+%5C%7D_%7Bi%3D1%7D%5EN)] 的均值为0、协方差矩阵为单位阵。为了让均值等于0，可以设置
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yRJU5zah-1643617651140)(https://www.zhihu.com/equation?tex=%5Cmu+%3D+%5Cfrac+%7B1%7D%7BN%7D+%5Csum_%7Bi%3D1%7D%5E%7BN%7Dx_%7Bi%7D%5Ctag%7B13%7D)]

下面求解 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aSD8Blal-1643617651141)(https://www.zhihu.com/equation?tex=W)] ，将原始数据的协方差记为

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DGBKXZuj-1643617651141)(https://www.zhihu.com/equation?tex=%5CSigma+%3D+%5Cfrac+%7B1%7D%7BN%7D+%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28x_%7Bi%7D-+%5Cmu%29%5ET%28x_%7Bi%7D-%5Cmu%29%5Ctag%7B14%7D)]

根据公式(10)可以得到 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QOvyGYXS-1643617651141)(https://www.zhihu.com/equation?tex=%5Cwidetilde%7B%5CSigma+%7D%3DW%5ET%5CSigma+W)] ，所以，我们的实际目标是 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-a6QIeTWF-1643617651141)(https://www.zhihu.com/equation?tex=W%5ET%5CSigma+W%3DI)] ，然后，可得

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DLDgvsyr-1643617651142)(https://www.zhihu.com/equation?tex=%5CSigma+%3D+%28W%5ET%29%5E%7B-1%7DW%5E%7B-1%7D%3D%28W%5E%7B-1%7D%29%5ETW%5E%7B-1%7D%5Ctag%7B15%7D)]

我们知道 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GcFueEgZ-1643617651142)(https://www.zhihu.com/equation?tex=%5CSigma)] 是一个正定对称矩阵，正定对称矩阵都具有如下形式的SVD分解

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hXnxYBr5-1643617651142)(https://www.zhihu.com/equation?tex=%5CSigma%3DU+%5CLambda+U%5ET%5Ctag%7B16%7D)]

其中 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-X5Prfybl-1643617651142)(https://www.zhihu.com/equation?tex=U)] 是一个正交矩阵， [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hOKsnjoM-1643617651143)(https://www.zhihu.com/equation?tex=%5CLambda)] 是一个正对角矩阵，则可以让 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NzpKmuj7-1643617651143)(https://www.zhihu.com/equation?tex=W%5E%7B-1%7D%3D%5Csqrt+%7B%5CLambda%7DU%5ET)] ，则可以得到

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Lp9RRJ9Q-1643617651143)(https://www.zhihu.com/equation?tex=W%3D%5Csqrt%7B%5CLambda%5E%7B-1%7D%7DU%5Ctag%7B17%7D)]

到这里关于Bert-whitening的介绍就结束了。

3、SimCSE

待补充…