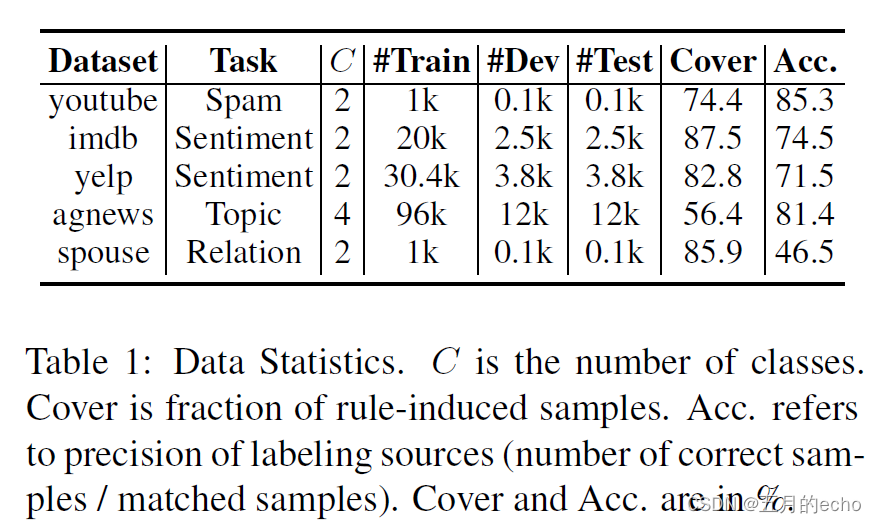
本文探究在没有标签情况下只使用易于提供的规则作为多个弱监督源的文本分类方法。使用诱导规则进行文本分类是具有挑战性的,因为,规则并不能覆盖一些长尾的样本,并且使用规则的学习往往是具有噪声的。为了解决这两个问题,本文设计了一种标签去噪器,利用条件软注意机制估计可靠性,然后通过聚合规则标注的弱标签来降低标签噪声。降噪后的伪标签监督神经分类器预测不匹配样本的软标签,解决了规则覆盖问题。
Preliminaries
假设存在多个弱监源,彼此提供互补的信息。下面提供了一个具体的例子:
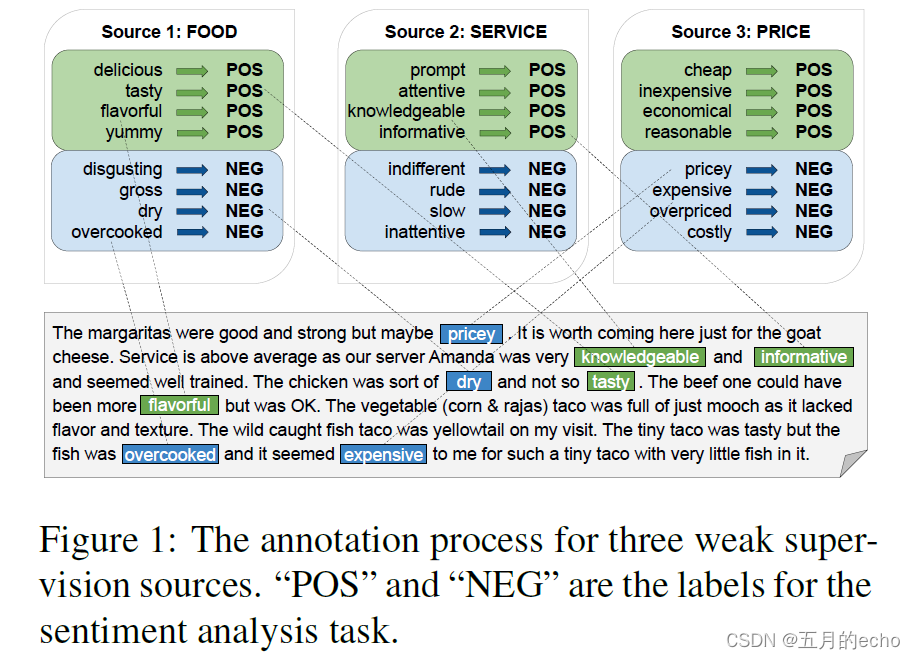
餐馆评价中涉及到的规则包含价格、服务、食物等多方面,这些源使用“if-else”标记函数从不同方面对领域知识进行编码。
Problem Formulation。形式上,方法需要一个待分类文档集合
D
=
{
d
1
,
d
2
.
.
.
d
n
}
D=\{d_1,d_2...d_n\}
D={d1?,d2?...dn?},目标类
C
=
{
C
1
,
C
2
.
.
.
C
m
}
C=\{C_1,C_2...C_m\}
C={C1?,C2?...Cm?},以及弱标记
S
=
{
R
1
,
R
2
.
.
.
R
k
}
S=\{R_1,R_2...R_k\}
S={R1?,R2?...Rk?},目标是从D学习一个只有多个弱监督源的分类器,以便对任何新到达的文档进行准确分类。
Method
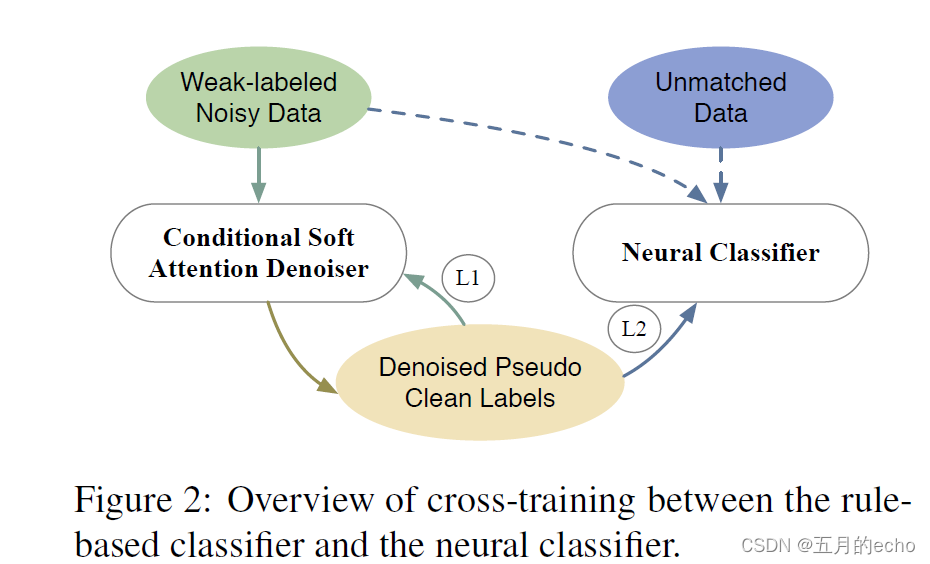
模型的总体框架如图所示。
首先,是一个标签去噪器来处理标签噪声问题,该去噪器迭代地去噪自己,以提高弱标签的质量。
其次是一个分类器,用于解决low coverage的问题。学习文本文档的分布式表示,并对每个文本文档进行分类,无论是否匹配规则。它既受到去噪后的弱标记数据的监督,也受到自己对不匹配数据的高自信预测的监督。更加细化的框架如下:
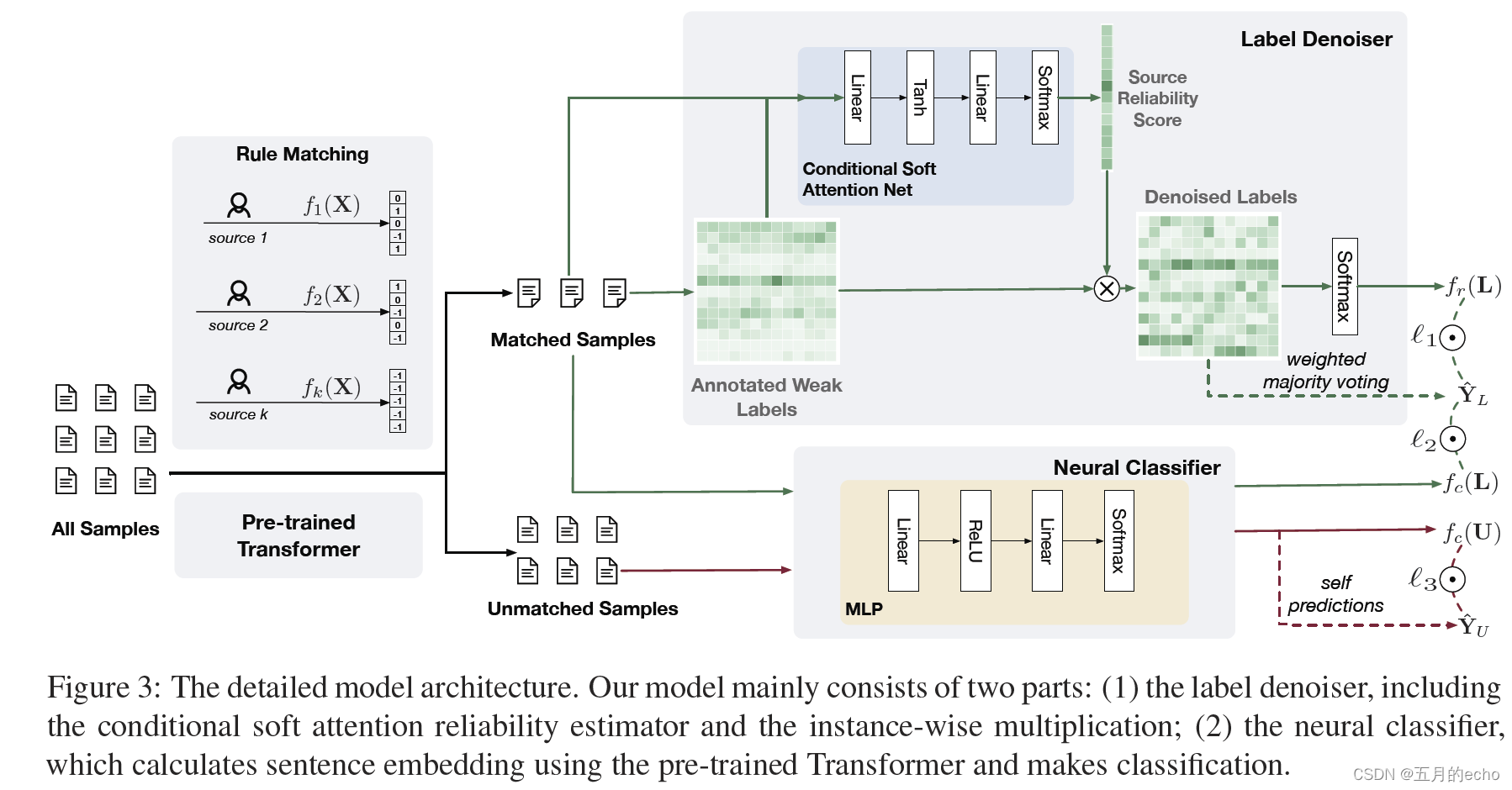
Label Denoiser
通过给定
k
k
k个labeling resources,可以通过规则匹配得到一个弱标签矩阵
Y
~
∈
R
n
?
k
?
\tilde Y\in R^{n*k*}
Y~∈Rn?k?。再以图一给出的例子举例,
k
=
3
k=3
k=3,并且由于是情感的二分类任务,
C
=
2
C=2
C=2。如果给定一句话“the food is tasty”,那么
k
1
k_1
k1?也就是food的标签为1,若是“gross”则为0。但是如果单词good并未出现在句子中,那么表示文档没有标签,也就是-1。以此类推,service以及price都会存在标签空间,最终得到一个三维的伪标签,比如[0,1,-1]。
为了进行标签去噪,降噪之后的标签表示为
Y
^
=
[
y
1
^
,
.
.
.
,
y
n
^
,
]
T
\hat Y=[\hat{y_1},..., \hat{y_n},]^T
Y^=[y1?^?,...,yn?^?,]T。
去噪网络本质上是一个两层的注意力网络,为每一个labeling source分配一个注意力得分
a
j
a_j
aj?:

其中
B
i
B_i
Bi?是通过encoder(Bert)学习到的特征向量。这里我觉得原文的公式有点问题,
y
~
i
,
j
\tilde y_{i,j}
y~?i,j?应该是一个数而非一个矩阵,因此要是写成"
y
~
i
+
B
i
\tilde y_{i}+B_i
y~?i?+Bi?"就合理一些了。有了注意力得分就可以计算注意力去噪之后的标签:
a
i
j
=
q
i
j
χ
C
(
y
~
i
,
j
≥
0
)
a_{ij}=q_{ij}\chi_C(\tilde y_{i,j} \geq 0)
aij?=qij?χC?(y~?i,j?≥0),这里
χ
C
\chi_C
χC?是一个指示函数。所有
n
n
n个样本的注意力可以组成一个矩阵
A
A
A,对每一个样本进行平均之后聚合得到reliability vector
A
=
{
a
1
,
a
2
,
.
.
.
,
a
k
}
A=\{a_1, a_2,..., a_k\}
A={a1?,a2?,...,ak?}。也就是说,最终每一个source对应一个评分。
得到了评分矩阵之后,就可以对样本进行降噪,其实就是与每一个样本对应的向量相乘:
Y
^
i
?
A
\hat Y_i \otimes A
Y^i??A。之后选择最大的概率得到预测的标签:
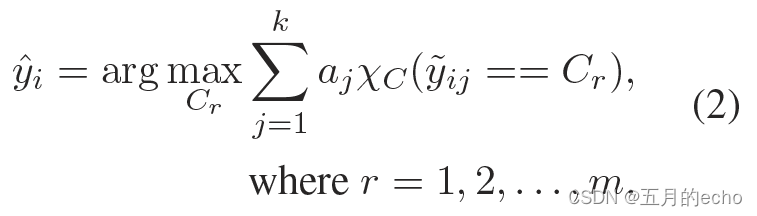
降噪之后的
Y
^
\hat Y
Y^进一步用于指导neural classifier,其对应的样本集合为
D
L
D_L
DL?。
此外,最终得到的
A
i
A_i
Ai?可以直接指导原
Y
~
i
\tilde Y_i
Y~i?进行特征学习:

此处的
?
\otimes
?定义如下:
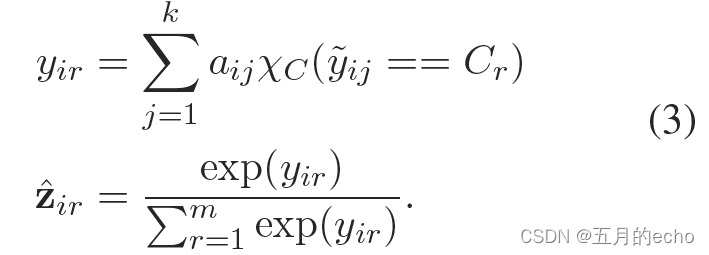
The Neural Classifier
神经分类器设计用于处理所有样本,包括匹配样本和不匹配样本(也就是规则不能涵盖的样本
D
U
D_U
DU?)。本文中分类器由Bert+2层MLP构成:

The Training Objective
l
1
l_1
l1?是由
D
L
D_L
DL?产出的去噪标签与
z
^
i
\hat z_i
z^i?共同优化的:

这是模型self-train的过程。而neural classifier在
D
L
D_L
DL?数据集上规定了另一个损失
l
2
l_2
l2?:

之后,在
D
U
D_U
DU?数据集上,neural classifier产出第三个self-train的损失
l
3
l_3
l3?。本文应用了时间集成策略,它将之前多个网络评估的预测聚合成一个集成预测,以缓解噪声传播:

Z
i
Z_i
Zi?是集成的结果,
α
\alpha
α用于控制集成的过程中考虑多少上一个step的特征。之后根据
Z
i
Z_i
Zi?构造
p
i
p_i
pi?:

之后最小化neural classifier的预测结果与
p
i
p_i
pi?的欧氏距离:

最终,总体的损失函数如下:

在预测的过程中,如果标签去噪器和神经分类器的两个预测发生冲突,选择可信度较高的预测,其中可信度得分为softmax输出。
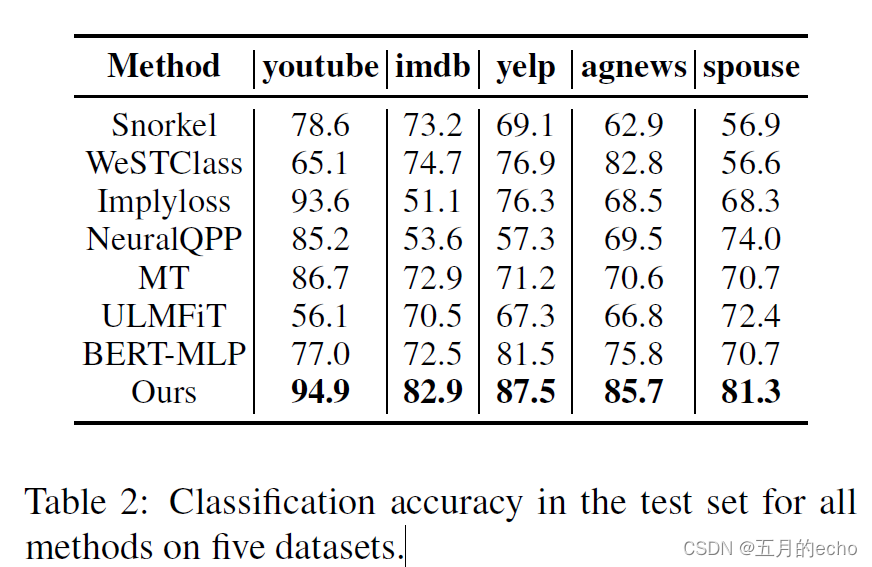
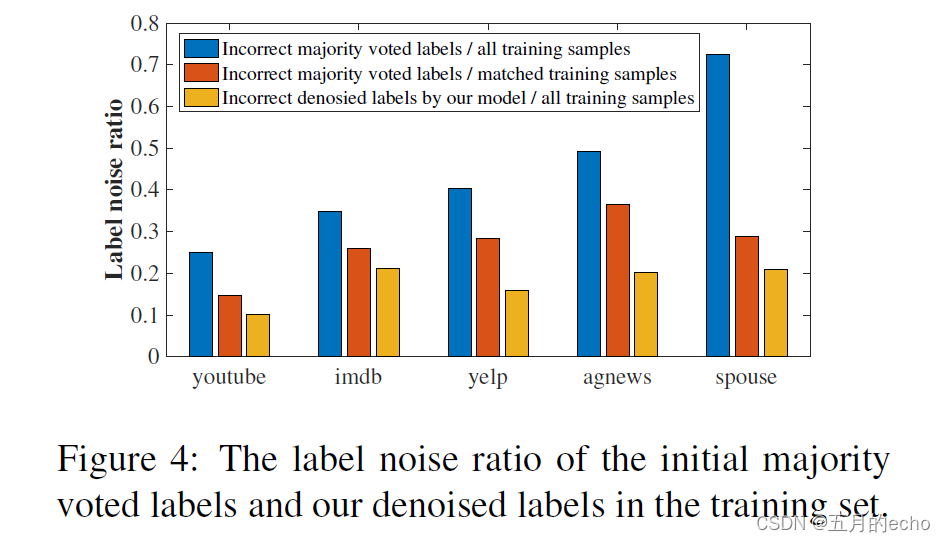
Experiments