[人工智能]XGBoost A Scalable Tree Boosting System

XGBoost: A Scalable Tree Boosting System 论文阅读笔记

作者：陈天奇 2016年发表

XGBoost 是大规模并行 boosting tree 的工具，它是目前最快最好的开源 boosting tree 工具包，比常见的工具包快 10 倍以上。xgboost 和 GBDT 两者都是 boosting 方法，除了工程实现、解决问题上的一些差异外，最大的不同就是目标函数的定义。

1.正则化目标函数

xgboost和GBDT等boosting算法一样，由$k$个基模型组成的加法运算式。$$\widehat{y_i}=?(x_i)=\sum _{k=1}^K{f}_k(x_i),f_k\in \mathcal{F}$$

其中$\mathcal{F}=\left\{f(x)=w_{q(x)}\right\}(q:R^m\to T,w\in R^T)$是回归树空间，其中$w_{q(x)}$代表样本$x$处在$q(x)$节点上，取值为权值$w_{q(x)}$，所以模型的目标函数为：

$$L(?)=\sum _{i=1}l(\widehat{y_i},y_i)+\sum _k\Omega (f_k)$$

其中$l$代表模型学习过程中设定的损失函数，可以为mae、mse等常见损失函数，第二项是正则项，为

$$\Omega (f)=\gamma T+\frac{1}{2}\lambda \Vert w{\Vert }^2$$, $w$为各个叶子节点的权重，类似与LR模型的权重。

因为模型是加法模型，我们可以二阶泰勒展开

$$L^t(?)=\sum _{i=1}l({\widehat{y_i}}^{(t)},y_i)+\sum _k\Omega (f_k)=\sum _{i=1}l({\widehat{y_i}}^{(t?1)}+f_t(x_i),y_i)+\sum _k\Omega (f_k)\approx \sum _{i=1}[(l({\widehat{y_i}}^{(t?1)},y_i)+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\sum _k\Omega (f_k)$$

其中$g_i={?}_{{\hat{y}}^{(t?1)}}l(y_i,{\hat{y}}^{(t?1)}){|}_{{\hat{y}}^{(t?1)}={\widehat{y_i}}^{(t?1)}}$， $h_i={?}_{{\hat{y}}^{(t?1)}}^{2}l(y_i,{\hat{y}}^{(t?1)}){|}_{{\hat{y}}^{(t?1)}={\widehat{y_i}}^{(t?1)}}$，因为此性质，xgb不仅可以用决策树当基分类器，也支持其他线性模型，只要满足一、二阶可导即可。

因为上式中$l({\widehat{y_i}}^{(t?1)},y_i)$是常数项， 我们的目标是最小化$L^t(?)$，所以可以舍去，就得到了我们需要最小化的目标函数，定义 I j = { i ∣ q ( x i ) = j } I_j=\left \{ i|q(x_i)=j\right\} Ij?={i∣q(xi?)=j}是叶子节点$j$的实例集合。

$$Ob{j}^{(t)}=\sum _{i=1}[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\sum _k\Omega (f_k)=\sum _{i=1}[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2=\sum _{j=1}^T[(\sum _{i\in I_j}{g}_i)w_j+\frac{1}{2}(\sum _{i\in I_j}{h}_i+\lambda )w_j^2]+\gamma T$$

所以在上式中只有$w_j$是未知数，对其求导等于0可得$w_j^{?}=\frac{{\sum }_{i\in I_j}{g}_i}{{\sum }_{i\in I_j}{h}_i+\lambda }$， 此时得到最优的$Ob{j}^{(t)}=?\frac{1}{2}{\sum }_{j=1}^T\frac{({\sum }_{i\in I_j}{g}_i{)}^2}{{\sum }_{i\in I_j}{h}_i+\lambda }+\lambda T$，利用该式来衡量树结构的好坏。数值越小，说明树越好。

计算$$Ob{j}_{split}=\frac{1}{2}[\frac{({\sum }_{i\in I_L}{g}_i{)}^2}{{\sum }_{i\in I_L}{h}_i+\lambda }+\frac{({\sum }_{i\in I_R}{g}_i{)}^2}{{\sum }_{i\in I_R}{h}_i+\lambda }?\frac{({\sum }_{i\in I}{g}_i{)}^2}{{\sum }_{i\in I}{h}_i+\lambda }]?\gamma$$，来找最优分割点。

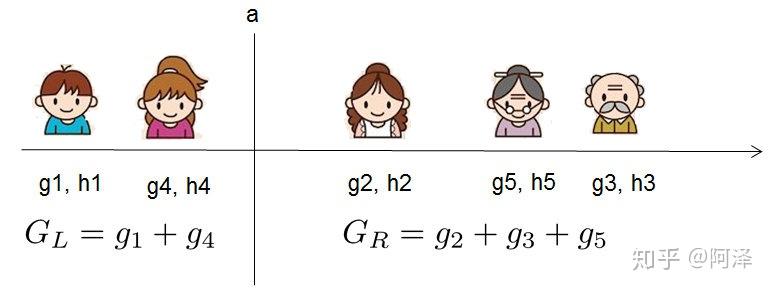
2.两种防止过拟合的方法

1. Shrinkage：类似学习率，对每个学习得到的树前乘一个权重$\eta$，以此增大后面的树学习空间。
2. Column Subsampling: 在随机森林使用的较多，这里也可以使用防止过拟合。

3.找分割点算法

1）贪心算法

遍历每个特征计算，找最优点即可

2）近似算法

对于海量数据而言，计算机没有足够的内存存储所有数据点，也就无法使用贪心算法。此时使用一种近似算法。

• 第一个 for 循环：对特征 k 根据该特征分布的分位数找到切割点的候选集合 S k = { s k 1 , s k 2 , ? ? , s k l } S_k=\{s_{k1}, s_{k2}, \cdots, s_{kl}\} Sk?={sk1?,sk2?,?,skl?}。XGBoost 支持 Global 策略和 Local 策略。
• 第二个 for 循环：针对每个特征的候选集合，将样本映射到由该特征对应的候选点集构成的分桶区间中，即 $s_{k,v}>=x_{jk}>=k,v?1$ ，对每个桶统计 $G,H$ 值，最后在这些统计量上寻找最佳分裂点。

对于每个特征，只考察分位点可以减少计算复杂度。

该算法会首先根据特征分布的分位数提出候选划分点，然后将连续型特征映射到由这些候选点划分的桶中，然后聚合统计信息找到所有区间的最佳分裂点。在提出候选切分点时有两种策略：

• Global：学习每棵树前就提出候选切分点，并在每次分裂时都采用这种分割；
• Local：每次分裂前将重新提出候选切分点。

直观上来看，Local 策略需要更多的计算步骤，而 Global 策略因为节点没有划分所以需要更多的候选点。

下图给出近似算法的具体例子，以三分位为例：

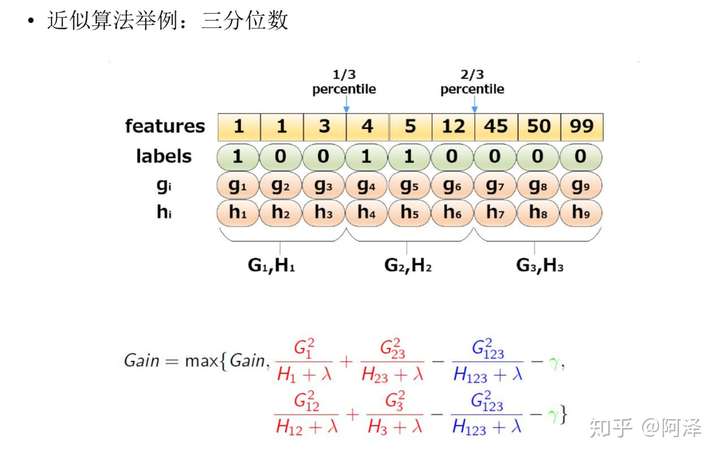
根据样本特征进行排序，然后基于分位数进行划分，并统计三个桶内的 $G,H$ 值，最终求解节点划分的增益。

加权分位数缩略图

事实上， XGBoost 不是简单地按照样本个数进行分位，而是以二阶导数值 [公式] 作为样本的权重进行划分，如下：

我们知道模型的目标函数为：
$$Ob{j}^{(t)}\approx \sum _{i=1}^n[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\sum _{i=1}^t\Omega (f_i)$$
我们稍作整理，便可以看出 $h_i$ 有对 loss 加权的作用。

$$\begin{array}{rl}Ob{j}^{(t)}& \approx \sum _{i=1}^n[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\sum _{i=1}^t\Omega (f_i)\\ & =\sum _{i=1}^n[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)+\frac{1}{2}\frac{g_i^2}{h_i}]+\Omega (f_t)+C\\ & =\sum _{i=1}^n\frac{1}{2}{h}_i[f_t(x_i)?(?\frac{g_i}{h_i}){]}^2+\Omega (f_t)+C\end{array}$$
其中 $\frac{1}{2}\frac{g_i^2}{h_i}$ 与 $C$ 皆为常数。我们可以看到 $h_i$ 就是平方损失函数中样本的权重。

对于样本权值相同的数据集来说，找到候选分位点已经有了解决方案（GK 算法），但是当样本权值不一样时，该如何找到候选分位点呢？（作者给出了一个 Weighted Quantile Sketch 算法，这里将不做介绍。）

4.稀疏感知算法

对于稀疏数据处理，xgb也提出了一种高效的处理算法，造成数据稀疏的三个原因：1）数据中缺失值较多，2）统计数据中0出现次数较多，3）人为编码造成0值很多，如one hot编码。

5.工程实现

参考https://zhuanlan.zhihu.com/p/87885678

6.优缺点

优点

1. 精度更高：GBDT 只用到一阶泰勒展开，而 XGBoost 对损失函数进行了二阶泰勒展开。XGBoost 引入二阶导一方面是为了增加精度，另一方面也是为了能够自定义损失函数，二阶泰勒展开可以近似大量损失函数；
2. 灵活性更强：GBDT 以 CART 作为基分类器，XGBoost 不仅支持 CART 还支持线性分类器，（使用线性分类器的 XGBoost 相当于带 L1 和 L2 正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题））。此外，XGBoost 工具支持自定义损失函数，只需函数支持一阶和二阶求导；
3. 正则化：XGBoost 在目标函数中加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、叶子节点权重的 L2 范式。正则项降低了模型的方差，使学习出来的模型更加简单，有助于防止过拟合；
4. Shrinkage（缩减）：相当于学习速率。XGBoost 在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间；
5. 列抽样：XGBoost 借鉴了随机森林的做法，支持列抽样，不仅能降低过拟合，还能减少计算；
6. 缺失值处理：XGBoost 采用的稀疏感知算法极大的加快了节点分裂的速度；
7. 可以并行化操作：块结构可以很好的支持并行计算。

缺点

1. 虽然利用预排序和近似算法可以降低寻找最佳分裂点的计算量，但在节点分裂过程中仍需要遍历数据集；

2. 预排序过程的空间复杂度过高，不仅需要存储特征值，还需要存储特征对应样本的梯度统计值的索引，相当于消耗了两倍的内存。

3. 虽然利用预排序和近似算法可以降低寻找最佳分裂点的计算量，但在节点分裂过程中仍需要遍历数据集；

4. 预排序过程的空间复杂度过高，不仅需要存储特征值，还需要存储特征对应样本的梯度统计值的索引，相当于消耗了两倍的内存。