系列文章目录
Python数据分析入门笔记1——学习前的准备
Python数据分析入门笔记2——pandas数据读取
Python数据分析入门笔记3——数据预处理之缺失值
Python数据分析入门笔记4——数据预处理之重复值
Python数据分析入门笔记
前言
异常值,指的是明显偏离它们所属样本的其余观测值的个别值。
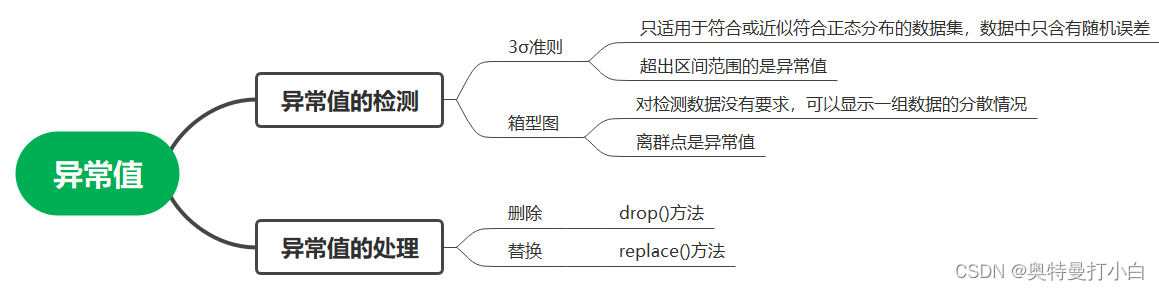
一、异常值的检测
1. 使用3σ准则检测异常值
(1)从数学概念开始,逐步理解:
1、标准差:所有数减去其平均值μ的平方和,所得结果除以该组数之个数(或个数减一,即变异数),再把所得值开根号,所得之数就是这组数据的标准差,记为σ。
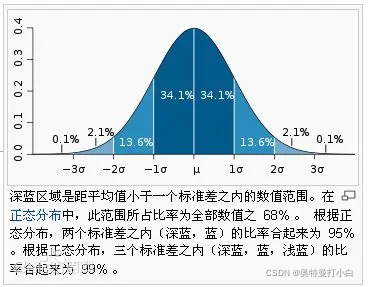
2、正态分布:正态分布是统计学中十分重要的概率分布。
简单来说,对于正态分布,数值接近平均值的概率最大,就像班级中一般90分以上和不及格的人数都比较少,中间分数的人数最多。
图上可以看到,正负三个标准差之内(深蓝,蓝,浅蓝)的比率合起来为99.6%。
也就是说,大部分数据都集中在(μ-3σ, μ+3σ)这个区间。
3、3σ原则,又叫拉依达原则,它是指假设一组检测数据中只含有随机误差,需要对其进行计算得到标准偏差,按一定概率确定一个区间,对于超过这个区间的误差,就不属于随机误差而是粗大误差,需要将含有该误差的数据进行剔除。
????所以我们初学者,就可以简单粗暴的认为,游离在大部队之外的,误差超过(μ-3σ, μ+3σ)区间的数值,都是异常值。
(2)代码实现如下:
假设有data.xlsx文件,记录了班级同学的成绩,部分数据如下:
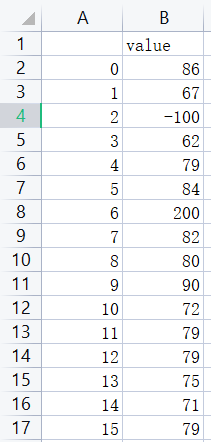
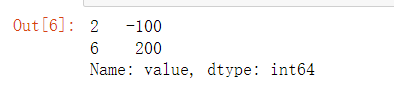
我们很明显看到行索引为2和行索引为6的分数值明显超出正常范围,所以我们希望通过3σ准则用代码把这两个“例外”找出来。
import numpy as np
import pandas as pd
def three_sigma(ser):
'''
ser参数:被检测的数据,接收DataFrame的一列数据
返回:异常值及其对应的行索引
'''
# 计算平均值
mean_data=ser.mean()
# 计算标准差
std_data=ser.std()
# 小于μ-3σ或大于μ+3σ的数据均为异常值
rule=(mean_data-3*std_data > ser) | (mean_data+3*std_data < ser)
# 然后np.arange方法生成一个从0开始,到ser长度-1结束的连续索引,再根据rule列表中的True值,直接保留所有为True的索引,也就是异常值的行索引
index=np.arange(ser.shape[0])[rule]
# 获取异常值
outliers=ser.iloc[index]
return outliers
# 读取data.xlsx文件
excel_data=pd.read_excel('D://Projects/data.xlsx')
# 对value列进行异常值检测,只要传入一个数据列
three_sigma(excel_data['value'])
输出结果:
(3)注意事项:只适用于正态分布的数据,并且数据量不能太少。
2. 使用箱型图检测异常值
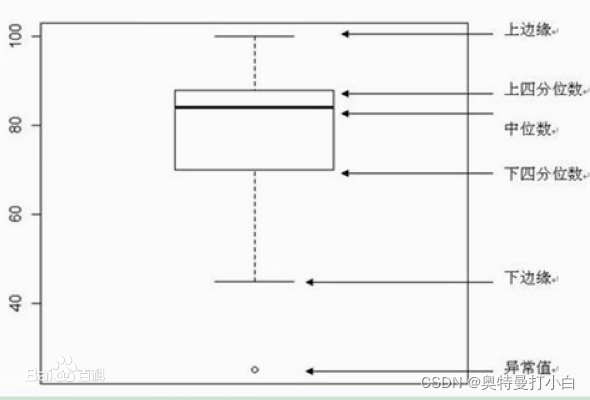
????箱型图是一种用于显示一组数据分散情况的统计图。基本结构如图所示:
主要包含六个数据节点,将一组数据从大到小排列,分别计算出他的上边缘,上四分位数Q3,中位数,下四分位数Q1,下边缘,还有一个异常值。
可以这样理解:
假设有一个数据集,有10万条数据,先将数据按从小到大的顺序排序
那么,前5万条数据的中位数就是Q3,后5万条数据的中位数就是Q1,四分位数间距IQR就是Q3-Q1。
异常值范围通常为小于Q1-1.5IQR,或者大于Q3+1.5IQR
为了能够直观地从箱型图中查看异常值,pandas中提供了两个用于绘制箱型图的函数——plot()和boxplot()。
plot()函数能够根据Series类对象和DataFrame类对象绘制箱型图,绘制的图表默认不显示网格线。
boxplot()函数只能根据DataFrame类对象绘制箱型图,默认显示网格线。
DataFrame.boxplot(column=None, by=None, ax=None, fontsize=None, rot=0, grid=True, figsize=None, layout=None, return_type=None, backend=None, **kwargs)
参数说明:
| 参数 | 说明 | 取值和解释 |
|---|---|---|
| column | 表示被检测的列名 | |
| fontsize | 表示箱型图坐标轴的字体大小。 | |
| rot | 表示箱型图坐标轴的旋转角度。 | |
| grid | 表示箱型图窗口的大小。 | |
| return_type | 表示返回的对象类型。 | ‘axes’,默认值,表示返回箱型图被绘制的绘图区域(matplotlib的Axes类对象)。 ‘dict’,返回一个字典,其值是箱型图的线条matplotlib的Line类对象。 ‘both’,表示返回一个包含Axes类对象和Line类对象的元组。 |
代码演示如下:
import pandas as pd
excel_data=pd.read_excel('D://Projects/data.xlsx')
# 根据data.xlsx文件中value列的数据,画一个箱型图
excel_data.boxplot(column='value')
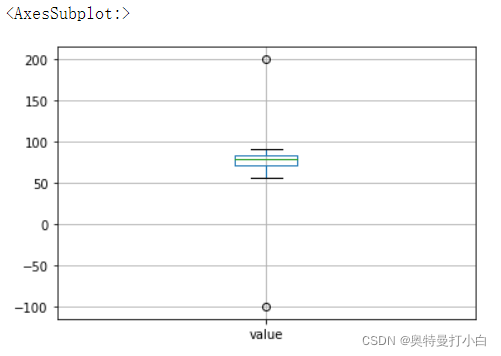
我们可以看到,两个圆圈表示的两个异常值。
代码实现:
1、定义一个从箱型图中获取异常值的函数box_outliners
2、返回文件中数据的异常值及其对应的索引
import pandas as pd
import numpy as py
def box_outliers(ser):
#对待检测的数据集进行排序
new_ser=ser.sort_values()
# 判断数据的总数量是奇数还是偶数
if new_ser.count()%2==0 :
#计算Q3,Q1,IQR
Q3=new_ser[int(len(new_ser)/2):].median()
Q1=new_ser[:int(len(new_ser)/2)].median()
elif new_ser.count()%2 !=0 :
Q3=new_ser[int(len(new_ser)/2-1):].median()
Q1=new_ser[:int(len(new_ser)/2-1)].median()
IQR=round(Q3-Q1,1)
rule=(round(Q3+1.5*IQR,1)<ser) | (round(Q1-1.5*IQR,1)>ser)
index=np.arange(ser.shape[0])[rule]
#获取异常值及其索引
outliers=ser.iloc[index]
return outliers
excel_data=pd.read_excel('D://Projects/data.xlsx')
box_outliers(excel_data['value'])
执行结果:
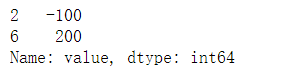
我们可以看到,用箱型图也能抓到这两个异常值。
与3σ准则不同的是,箱型图并不局限于正态分布,任何数据集都可以用箱型图来检测。
二、异常值的处理
异常值被检测出来之后,还需要进一步确认,确认是真正的异常值才会处理。
常用处理方式:
- 删除异常值——drop()方法
- 替换异常值——replace()方法
1. 删除异常值——drop()方法
pandas提供drop()方法,可按指定行索引或列索引来删除异常值。
DataFrame.drop(labels=None, axis=0, index=None, columns=None, level=None, inplace=False, errors=‘raise’)
| 参数 | 说明 | 取值和解释 |
|---|---|---|
| labels | 表示要删除的行索引或列索引,可以删除一个或多个。 | 例如删除第一行和第二行:df.drop([0,1]) |
| axis | 指定删除行或删除列 | 0或’index’,删除行。 1或’columns’,删除列。 |
| index | 指定要删除的行 | |
| columns | 指定要删除的列 |
删除异常值后,可以再次调用自定义的异常值检测函数,以确保数据中的异常值全部被删除,代码演示如下:
# 根据上面自定义函数得到的异常值行索引,来删除异常值
clean_data=excel_data.drop([2,6])
# 再次检测数据中是否还有异常值
three_sigma(clean_data['value'])
输出:Series([], Name: value, dtype: int64)
则说明异常值已经全部删除成功
2. 替换异常值——replace()方法
DataFrame.replace(to_replace=None, Value=None, inplace=False, limit=None, regex=False, method=‘pad’)
| 参数 | 说明 | 取值和解释 |
|---|---|---|
| to_place | 表示被替换的值。 | |
| value | 表示被替换后的值,默认为None。 | |
| inplace | 表示是否修改原数据。 | True,表示直接修改原数据; False,表示修改原数据的副本。 |
| method | 表示替换方式。 | ‘pad/ffill’,向前填充 ’bfill’,向后填充。 |
假设要对前面的成绩单异常值进行处理,负值处理为0分,超过100分的统一按100分计算。
代码演示如下:
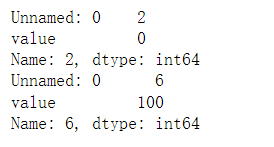
replace_data=excel_data.replace({-100:0,200:100})
# 根据行索引获取替换后的值
print(replace_data.loc[2])
print(replace_data.loc[6])
执行结果:
总结
需要掌握的:
-
3σ准则检测异常值的思路:
- 确认数据集是否为正态分布,正态分布的数据集才能继续。
- 计算需要检验的数据列的平均值mean_data和标准差std_data;
- 写一个3σ检测函数,传入一个DataFrame对象的一个列,
方法中,先看数据列的每个值,小于μ-3σ或大于μ+3σ的数据均为异常值,返回异常值系列。 - 如果是真实异常值,则剔除异常值,得到规范的数据。
-
箱型图检测异常值的思路:
- 编写一个箱型图检测函数,将数据从小到大排序,前一半数据的中位数,就是下四分位数Q1,后一半数据的中位数,就是上四分位数Q3,然后看数据列的每个值,小于Q1-1.5IQR或者大于Q3+1.5IQR的值均为异常值,返回异常值系列。
- 如果是真实异常值,则提出异常值,得到规范的数据。