变换2
第三讲的补充:旋转矩阵的逆矩阵与旋转矩阵的转置矩阵相同。
一、3D变换(3D Transformations)
(1)3D场景中放缩和平移对应的变换矩阵如下。
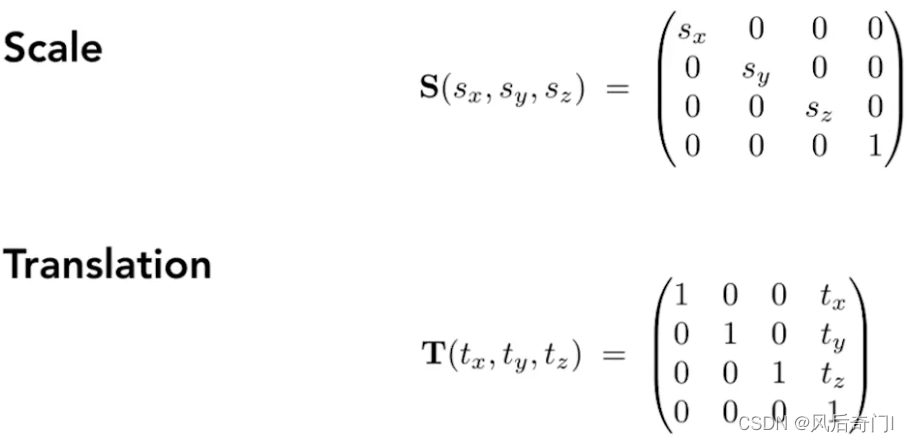
(2)3D场景中仅绕一个轴旋转对应的变换矩阵如下。
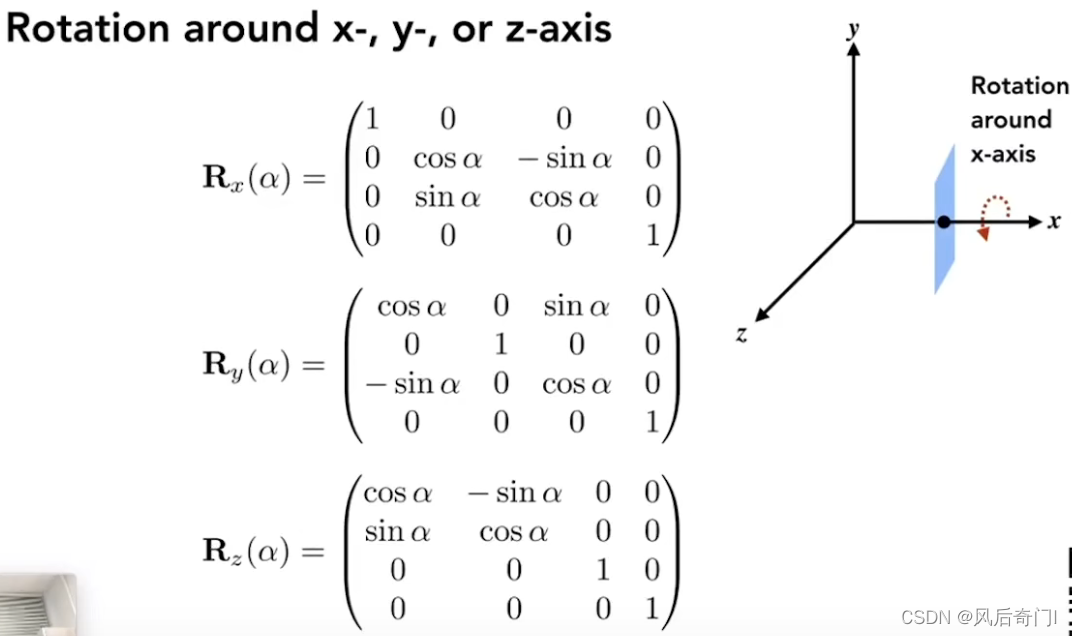
①可以发现绕y轴旋转有些不同,这是跟坐标系的方向有关。
②老师的解释:根据xyz的顺序,前两个的叉乘可以得到后一个,如xy叉乘可以得到z,yz叉乘可以得到x,而zx叉乘才可以得到y,而变换矩阵的顺序是xz,因此是相反的顺序。
(3)3D场景中任意旋转
①如下图,以飞机为例子可以直观地理解3D场景的旋转。绕任意轴的旋转通常是将其分解到xyz轴上依次进行旋转。
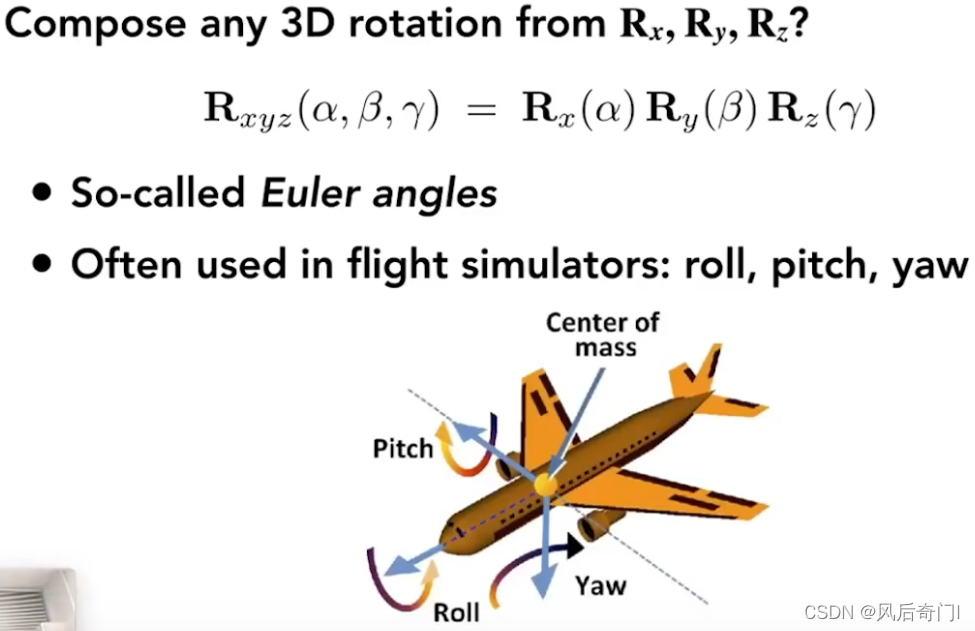
②绕任意轴n旋转α的变换矩阵计算公式如下:

二、观测变换(Viewing Transformation)
(1)观测变换由视图变换(View(视图)/Camera transformation)和投影变换(Projection Transformation)两类组成。
(2)思考如何拍一张照片?
①需要一个好的场景以及安排每个人/物的位置。(模型变换model transformation)
②需要一个好的角度放置相机。(视图变换view transformation)
③拍照。(投影变换projection transformation)
三、View(视图)/Camera transformation
(1)首先需要考虑相机的设置:
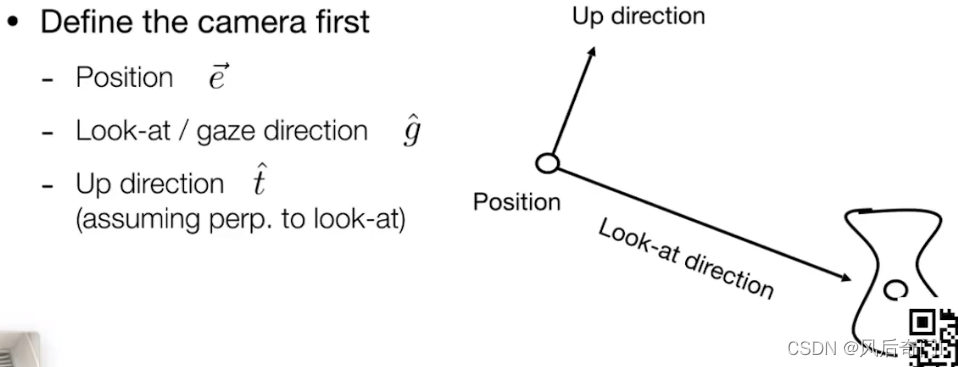
①主要涉及到三点:相机的位置、相机镜头的朝向、相机上方朝向(可以理解为头的左右旋转)。
②如果相机和物体同速率移动,获得的照片是相同的。
③相机的默认设置:位于(0,0,0),相机镜头朝向-Z轴,相机上方朝向方向为Y轴。
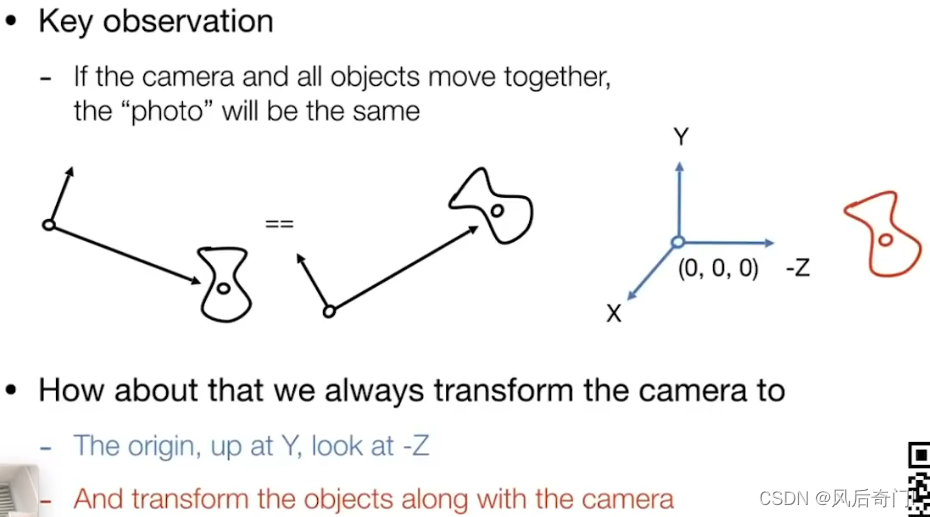
(2)如何将相机变为默认设置?
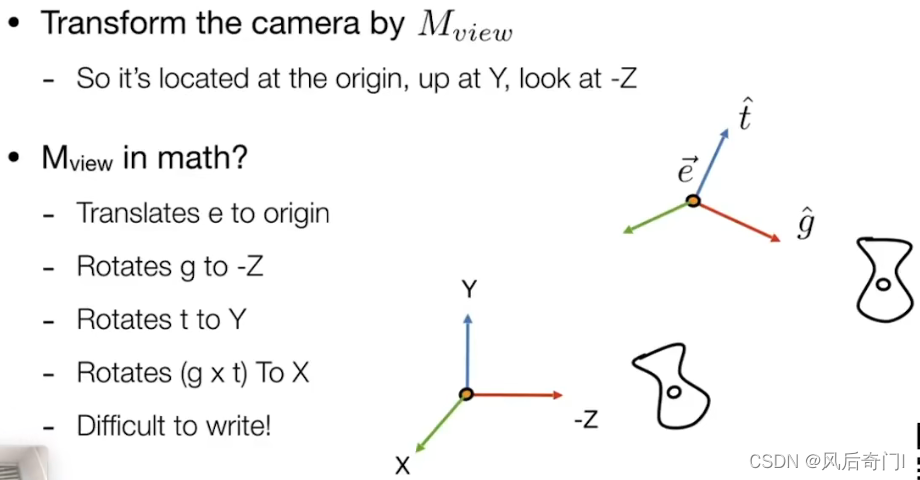
①使用Mview矩阵来进行变换。
②Mview矩阵的计算过程如下图。

③想将某个轴旋转到XYZ轴的旋转矩阵不容易写。但从XYZ轴旋转过去的旋转矩阵比较容易得到,因此可以先获得这个矩阵,在对其求逆矩阵即可得到需要的旋转矩阵。(旋转矩阵的逆矩阵与其转置矩阵相同)
(3)总结

四、投影变换(Projection Transformation)
(1)投影变换分为两种:正交投影和透视投影。


①透视投影有近大远小的现象。
五、正交投影(Orthographic projection)
(1)举个简单的例子理解。

①将相机移到默认位置。
②去掉Z轴的部分。
③将图形进行平移和放缩即可得到正交投影。
(2)举个通用的正规例子理解,目标是将一个长方体移到坐标系正中间并且变成一个标准的标准正方体。

①将长方体移到坐标系正中间。
②将长方体压缩成标准正方体。
(3)需要注意的是,X轴为左小右大,Y轴为下小上大,而Z轴为远小近大。
(4)正交投影的变换矩阵如下,先进行平移操作,后进行放缩操作。

六、透视投影(Perspective projection)
(1)透视投影的特点
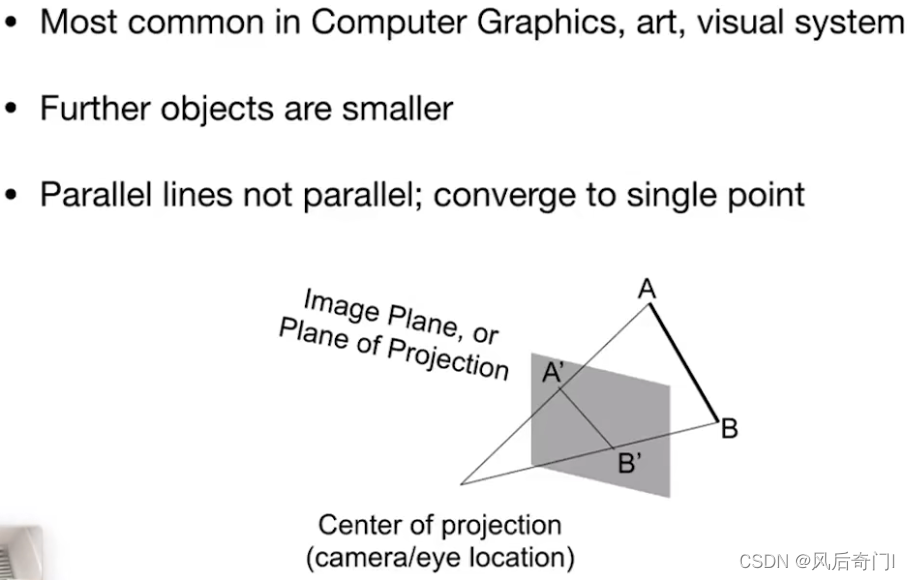
①近大远小。
②平行线相交于一点。
(2)如何获得透视投影?

①将上图左侧的截头锥体压成长方体。(n平面不变,f平面压缩到与n平面一样大,n平面与f平面的距离保持不变,即n平面和f平面上的点z轴坐标不发生变化,但两个平面间的点的z轴坐标会变化!)
②做正交投影。
(3)压缩操作的坐标变换矩阵推导
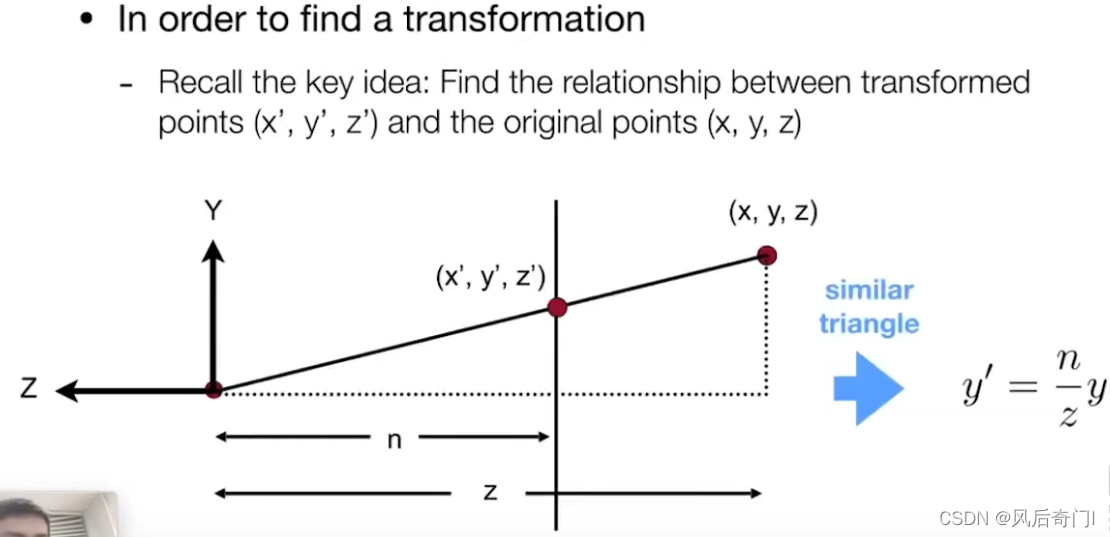
①n平面与f平面的x和y的坐标关系可以通过相似三角形得到。

②变化后的齐次坐标如图,其中z未知。

③接下来求原齐次坐标到压缩齐次坐标之间的变换矩阵,此时可以得到变换矩阵的大部分内容,还剩下第三行的数值。

④n平面的点的z轴坐标保持不变,因此可以得到上图。

⑤f平面的点的z轴坐标保持不变,因此可以得到上图。

⑥联立可解出A和B,综上可得变换矩阵。