6、线性回归
6.1 线性回归模型
6.1.1 线性回归模型简介
线性回归,就是能够用一个直线较为精确地描述数据之间的关系。这样当出现新的数据的时候,就能够预测出一个简单的值。线性回归中最常见的就是房价的问题。一直存在很多房屋面积和房价的数据,如下图所示:
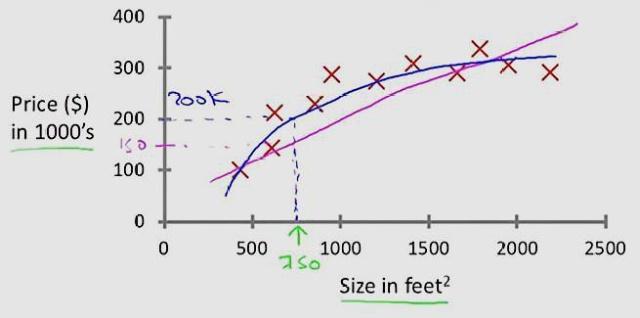
在这种情况下,就可以利用线性回归构造出一条直线来近似地描述放假与房屋面积之间的关系,从而就可以根据房屋面积推测出房价。
6.1.2线性回归的函数模型
事实上,限于机器学习的年轻(相比于数学,统计学,生物学等),机器学习很多的方法都是来自于其它领域,线性回归也不例外,它是来自于统计学的一个方法。
定义:给定数据集D={(x1, y1), (x2, y2), ... },我们试图从此数据集中学习得到一个线性模型,这个模型尽可能准确地反应x(i)和y(i)的对应关系。这里的线性模型,就是属性(x)的线性组合的函数,可表示为:
![]()
向量表示为:
![]()
其中,w=(w1; w2;w3; ..., wd) 表示列向量(; 为行分隔)
这里w表示weight,权重的意思,表示对应的属性在预测结果的权重,这个很好理解,权重越大,对于结果的影响越大;更一般化的表示是theta,是线性模型的参数,用于计算结果。
那么通常的线性回归,就变成了如何求得变量参数的问题,根据求得的参数,我们可以对新的输入来计算预测的值。(也可以用于对训练数据计算模型的准确度)
通俗的理解:x(i)就是一个个属性(例如西瓜书中的色泽,根蒂;Andrew ng示例中的房屋面积,卧室数量等),theta(或者w/b),就是对应属性的参数(或者权重),我们根据已有数据集来求得属性的参数(相当于求得函数的参数),然后根据模型来对于新的输入或者旧的输入来进行预测(或者评估)。
6.2 线性回归损失函数
以简单的一元线性回归(一元代表只有一个未知自变量)为例。
有n组数据,自变量x(x1,x2,…,xn),因变量y(y1,y2,…,yn),然后我们假设它们之间的关系是:f(x)=ax+b。那么线性回归的目标就是如何让f(x)和y之间的差异最小,换句话说就是a,b取什么值的时候f(x)和y最接近。
这里我们得先解决另一个问题,就是如何衡量f(x)和y之间的差异。在回归问题中,均方误差是回归任务中最常用的性能度量(自行百度一下均方误差)。记J(a,b)为f(x)和y之间的差异,即
i代表n组数据中的第i组。
这里称J(a,b)为损失函数,明显可以看出它是个二次函数,即凸函数(这里的凸函数对应中文教材的凹函数),所以有最小值。当J(a,b)取最小值的时候,f(x)和y的差异最小,然后我们可以通过J(a,b)取最小值来确定a和b的值。
到这里可以说线性回归就这些了,只不过我们还需要解决其中最关键的问题:确定a和b的值。
下面介绍三种方法来确定a和b的值:
6.2.1 最小二乘法
既然损失函数J(a,b)是凸函数,那么分别关于a和b对J(a,b)求偏导,并令其为零解出a和b。这里直接给出结果:
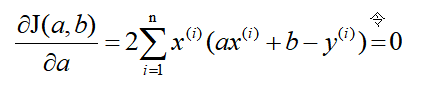
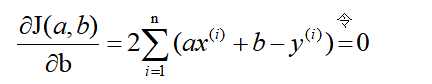
解得:
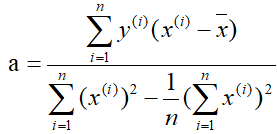
?
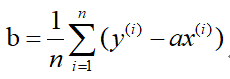
6.2.2梯度下降法
首先你得先了解一下梯度的概念:梯度的本意是一个向量(矢量),表示某一函数(该函数一般是二元及以上的)在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
当函数是一元函数时,梯度就是导数。这里我们用一个最简单的例子来讲解梯度下降法,然后推广理解更为复杂的函数。
还是用上面的例子,有n组数据,自变量x(x1,x2,…,xn),因变量y(y1,y2,…,yn),但这次我们假设它们之间的关系是:f(x)=ax。记J(a)为f(x)和y之间的差异,即:
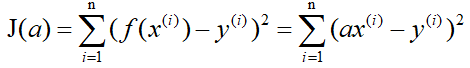
?在梯度下降法中,需要我们先给参数a赋一个预设值,然后再一点一点的修改a,直到J(a)取最小值时,确定a的值。下面直接给出梯度下降法的公式(其中α为正数):

?下面解释一下公式的意义,J(a)和a的关系如下图:
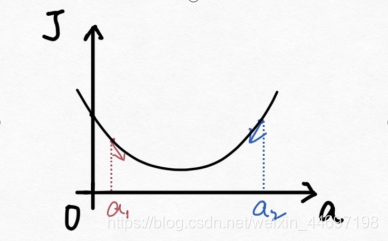
?假设给a取的预设值是a1的话,那么a对J(a)的导数为负数,则

也为负数,所以

?意味着a向右移一点。然后重复这个动作,直到J(a)到达最小值。
同理,假设给a取的预设值是a2的话,那么a对J(a)的导数为正数,则

意味着a向左移一点。然后重复这个动作,直到J(a)到达最小值。
所以我们可以看到,不管a的预设值取多少,J(a)经过梯度下降法的多次重复后,最后总能到达最小值。
这里再举个生活中的栗子,梯度下降法中随机给a赋一个预设值就好比你随机出现在一个山坡上,然后这时候你想以最快的方式走到山谷的最低点,那么你就得判断你的下一步该往那边走,走完一步之后同样再次判断下一步的方向,以此类推就能走到山谷的最低点了。而公式中的α我们称它为学习率,在栗子中可以理解为你每一步跨出去的步伐有多大,α越大,步伐就越大。(实际中α的取值不能太大也不能太小,太大会造成损失函数J接近最小值时,下一步就越过去了。好比在你接近山谷的最低点时,你步伐太大一步跨过去了,下一步往回走的时候又是如此跨过去,永远到达不了最低点;α太小又会造成移动速度太慢,因为我们当然希望在能确保走到最低点的前提下越快越好。)
到这里,梯度下降法的思想你基本就理解了,只不过在栗子中我们是用最简单的情况来说明,而事实上梯度下降法可以推广到多元线性函数上,这里直接给出公式,理解上(需要你对多元函数的相关知识有了解)和上面的栗子殊途同归。
假设有n组数据,其中目标值(因变量)与特征值(自变量)之间的关系为:
![]()
?其中i表示第i组数据,损失函数为:
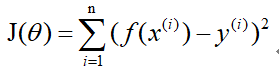
?梯度下降法:
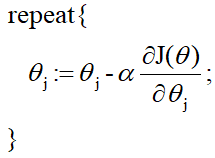
6.2.3 总结
- 梯度下降法是通用的,包括更为复杂的逻辑回归算法中也可以使用,但是对于较小的数据量来说它的速度并没有优势。
- 正规方程的速度往往更快,但是当数量级达到一定的时候,还是梯度下降法更快,因此没有详细介绍。因为正规方程中需要对矩阵求逆,而求逆的时间复杂的是n的3次方。
- 最小二乘法一般比较少用,虽然它的思想比较简单,在计算过程中需要对损失函数求导并令其为0,从而解出系数θ。但是对于计算机来说很难实现,所以一般不使用最小二乘法。
6.3 过拟合与欠拟合
6.3.1 欠拟合
模型过于简单,在训练集、测试集中表现都差
原因:学习到数据的特征过少
解决:
(1)增加特征数
通过“组合”、“泛化”、“相关性”来添加特征,同时,“上下文特征”、“平台特征”也是添加时的首选项
(2)添加多项式特征
在机器学习算法中使用的很普遍,例如线性回归时通过添加二次项或三次项来使模型泛化能力变强。
6.3.2 过拟合
模型过于复杂,在训练集中表现很好,测试集中表现很差
原因:原始特征过多,存在嘈杂特征,模型尝试兼顾所有特征
解决:
(1)重新清洗数据
过拟合也可能是由于数据不纯造成的,所以要重新清洗数据
(2)增大训练量
(3)正则化
(4)减少特征维度,防止维灾难(随纬度上升,分类器性能先上升,到达一点后便不断下降)
6.4 正则化
6.4.1 正则化
介绍:有些数据特征影响模型的复杂度,或者这个特征异常点较多,就要尽量减小这个特征的影响(甚至删除这个特征)
正则化力度越大,权重系数就越小
正则化力度越小,权重系数就越大
6.4.2 LASSO回归
L1回归
可以使某些w的值为0,删除其影响,倾向于消除完全不重要的权重
可以自动做出选择,输出一个稀疏模型(只有少数特征的权重为非0)
缺点:
在特征维度高于样本数或特征强相关时表现不佳
 ?
?
目标应使损失函数最小(minJ(θ)),所以使用一个较大的α就可以有效抑制θ的大小
API
from sklearn.linear_model import Lasso?6.4.3 Ridge Regression(岭回归)
L2回归
可以使某些w的值很小,趋近于0,削弱其影响
使用:添加α(惩罚力度),α越大,θ就越小

API:
from sklearn.linear_model import Ridge参数
fit_intercept=True:是否计算偏置
alpha=1.0:正则化力度(惩罚力度)0~ 1、1~10
solver:自动选择优化算法,若数据集大,数据多,一般自动选择sag(随即平均梯度下减)
normalize=True:是否进行标准化
属性
Ridge.coef_:回归权重
Ridge.intercept_:回归偏置
API:
from sklearn.linear_model import RidgeCV封装了交叉验证
增加参数alphas,可传入超参数组,进行交叉验证
6.4.4 Elastic net(弹性网络)
使用较为广泛

API:
from sklearn.linear_model import ElasticNet一般来说,我们应该避免使用朴素线性回归,对模型进行一定的正则化处理
6.5 案例
?6.5.1 数据来源
也可使用sklearn内置数据集load_boston
6.5.2 回归性能评估
回归性能评估:

?sklearn回归评估api:

6.5.3 正规方程求解代码
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, classification_report
from sklearn.externals import joblib
import pandas as pd
import numpy as np
def mylinear():
"""
线性回归直接预测房子价格
:return: None
"""
# 获取数据
lb = load_boston()
# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
print(y_train, y_test)
# 进行标准化处理(?) 目标值处理?
# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1)) #要是二维的
y_test = std_y.transform(y_test.reshape(-1, 1))
# estimator预测
# 正规方程求解方式预测结果
lr = LinearRegression()
lr.fit(x_train, y_train)
print(lr.coef_)
# 保存训练好的模型
# joblib.dump(lr, "./tmp/test.pkl")
# 预测测试集的房子价格
y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
print("正规方程测试集里面每个房子的预测价格:", y_lr_predict)
print("正规方程的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
if __name__ == "__main__":
mylinear()6.5.4 梯度下降代码
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, classification_report
from sklearn.externals import joblib
import pandas as pd
import numpy as np
def mylinear():
"""
线性回归直接预测房子价格
:return: None
"""
# 获取数据
lb = load_boston()
# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
print(y_train, y_test)
# 进行标准化处理(?) 目标值处理?
# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1)) #要是二维的
y_test = std_y.transform(y_test.reshape(-1, 1))
#梯度下降去进行房价预测
sgd = SGDRegressor()
sgd.fit(x_train, y_train)
print(sgd.coef_)
# 预测测试集的房子价格
y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
print("梯度下降测试集里面每个房子的预测价格:", y_sgd_predict)
print("梯度下降的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
if __name__ == "__main__":
mylinear()6.5.5 岭回归代码
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, classification_report
from sklearn.externals import joblib
import pandas as pd
import numpy as np
def mylinear():
"""
线性回归直接预测房子价格
:return: None
"""
# 获取数据
lb = load_boston()
# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
print(y_train, y_test)
# 进行标准化处理(?) 目标值处理?
# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1)) #要是二维的
y_test = std_y.transform(y_test.reshape(-1, 1))
# 岭回归去进行房价预测
rd = Ridge(alpha=1.0)
rd.fit(x_train, y_train)
print(rd.coef_)
# 预测测试集的房子价格
y_rd_predict = std_y.inverse_transform(rd.predict(x_test))
print("梯度下降测试集里面每个房子的预测价格:", y_rd_predict)
print("梯度下降的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))
if __name__ == "__main__":
mylinear()