文章目录
指数加权平均值Exponentially weighted averages
v
0
=
0
v
1
=
β
v
0
+
(
1
?
β
)
θ
1
v
t
=
β
v
t
?
1
+
(
1
?
β
)
θ
t
v_0 = 0\\ v_1 = \beta v_0 + (1-\beta)\theta_1\\v_t = \beta v_{t-1} + (1-\beta)\theta_{t}
v0?=0v1?=βv0?+(1?β)θ1?vt?=βvt?1?+(1?β)θt?
其
中
v
表
示
第
t
个
平
均
值
,
θ
t
表
示
第
t
个
值
,
β
是
需
要
选
定
的
超
参
数
,
大
致
可
以
理
解
为
我
们
需
要
考
虑
1
1
?
β
个
之
前
的
值
的
影
响
其中v表示第t个平均值,\theta_t表示第t个值,\beta\\ 是需要选定的超参数,大致可以理解为我们需要\\考虑\frac{1}{1-\beta}个之前的值的影响
其中v表示第t个平均值,θt?表示第t个值,β是需要选定的超参数,大致可以理解为我们需要考虑1?β1?个之前的值的影响
在机器学习和深度学习中,如果某个值既需要考虑以往的影响,又需要结合当前的价值,那么可以考虑使用加权平均数。
可以将
v
v
v想象为速度,将
θ
\theta
θ想象为加速度,当前的速度受到前一时间的速度和当前的加速度的影响。
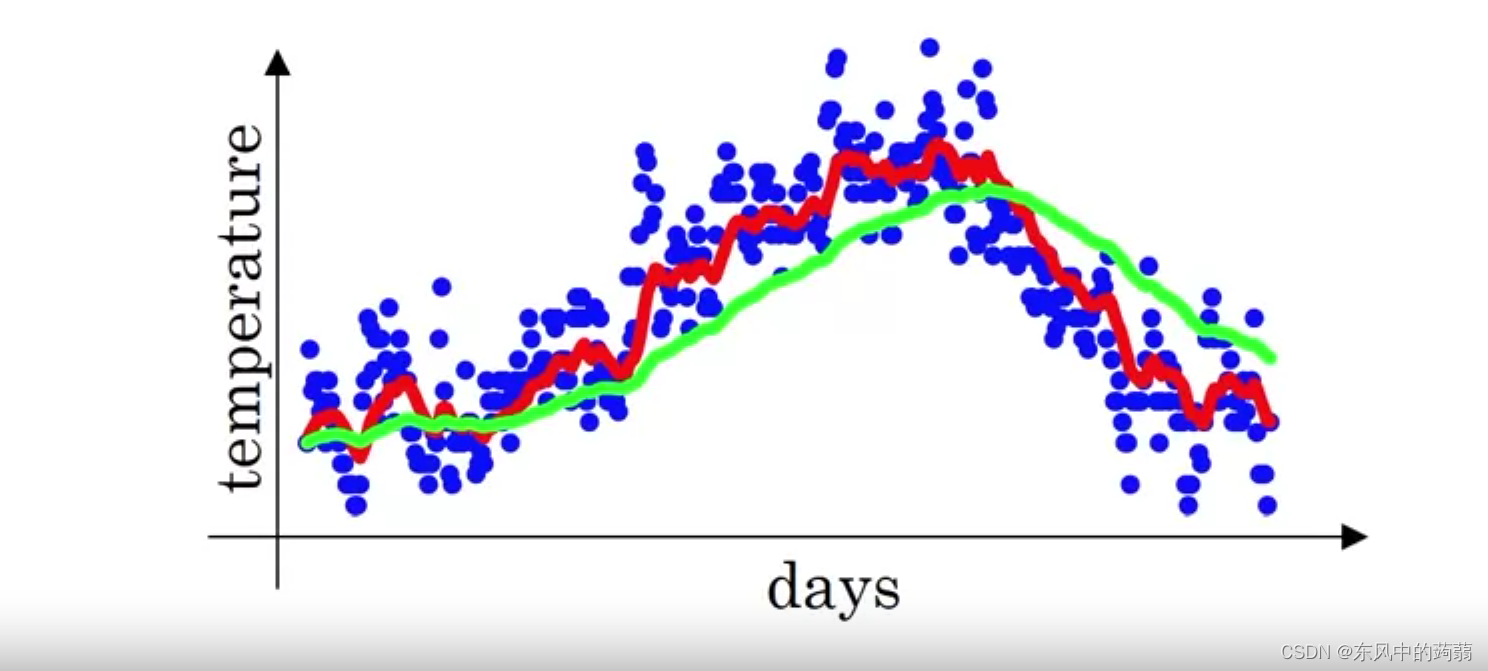
上图是对温度和天气使用指数加权平均数进行预测。其中红色的 β 1 \beta_1 β1?选用的值更低,绿色的 β 2 \beta_2 β2?更高
假定 β = 0.2 \beta=0.2 β=0.2
v 1 = 0.2 θ 1 v 2 = 0.16 θ 1 + 0.2 θ 2 v_1 = 0.2\theta_1\\ v_2 = 0.16\theta_1 + 0.2\theta_2 v1?=0.2θ1?v2?=0.16θ1?+0.2θ2?
可以看出上述平均值在
t
t
t很小的时候,该平均值不能很好拟合原模型,于是引入修正方法
v
0
=
0
v
1
c
o
r
r
e
c
t
e
d
=
v
1
1
?
β
1
.
.
.
v
t
c
o
r
r
e
c
t
e
d
=
v
t
1
?
β
t
v_0 = 0\\v_1^{corrected} = \frac{v_1}{1-\beta^{1}}\\...\\v_t^{corrected} = \frac{v_t}{1-\beta^t}
v0?=0v1corrected?=1?β1v1??...vtcorrected?=1?βtvt??
在之后将要介绍的三种优化器都是使用上述的类似方法进行优化。
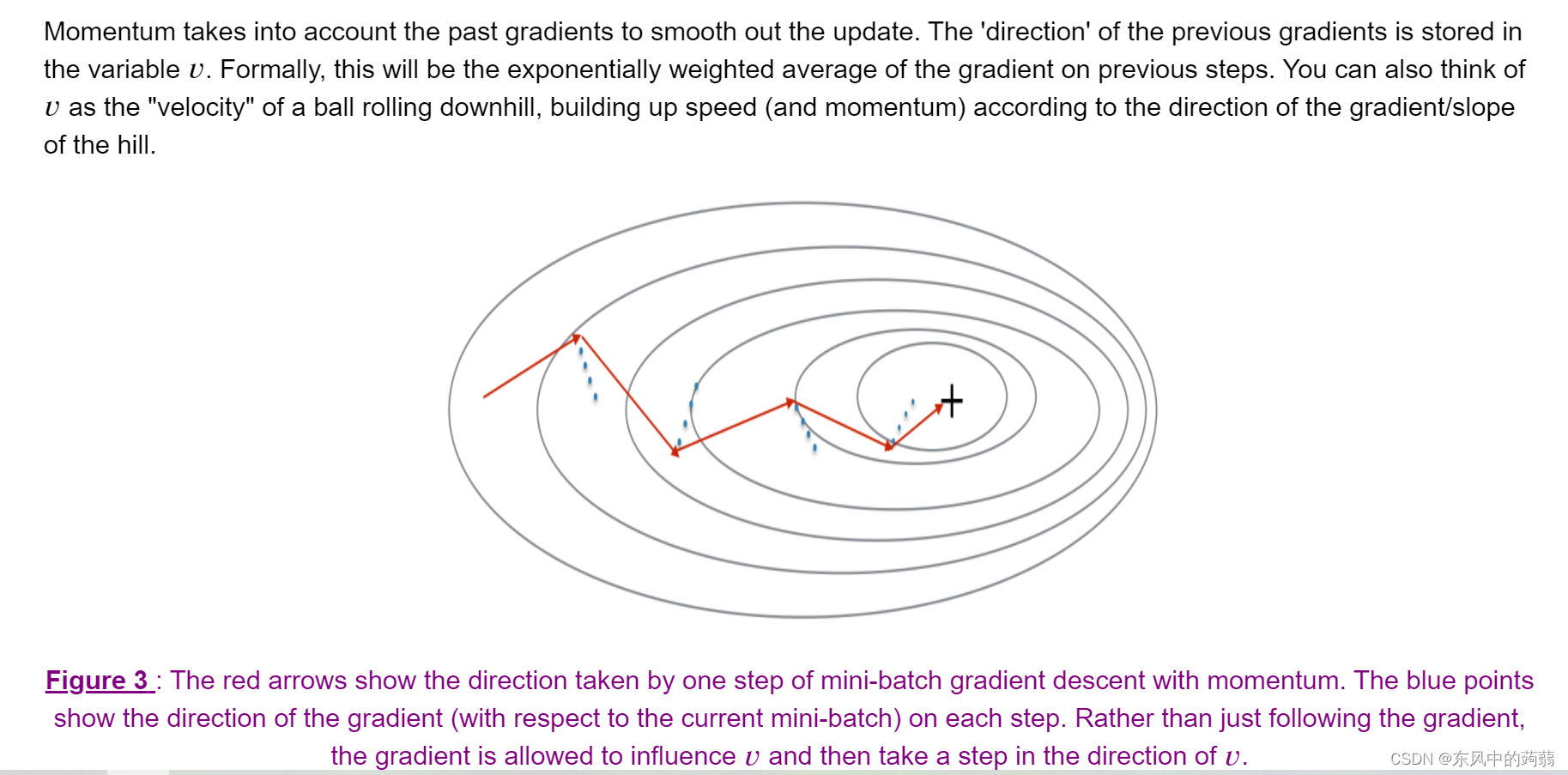
带动量的梯度下降方法(Gradient Descent with Momentum)
相比于传统的梯度下降算法,这个新的算法引入了动量,
我们有
p
a
r
a
n
e
w
=
p
a
r
a
o
l
d
?
α
g
r
a
d
其
中
α
为
学
习
率
。
para_{new} = para_{old} - \alpha grad\\其中\alpha为学习率。
paranew?=paraold??αgrad其中α为学习率。
而动量采用了我们前面所谈到的指数加权平均数
第
t
次
迭
代
的
更
新
公
式
为
:
p
a
r
a
n
e
w
=
p
a
r
a
o
l
d
?
α
v
t
v
t
=
β
v
t
?
1
+
(
1
?
β
)
g
r
a
d
t
第t次迭代的更新公式为:\\ para_{new} = para_{old} - \alpha v_t\\ v_t = \beta v_{t-1} + (1-\beta) grad_t\\
第t次迭代的更新公式为:paranew?=paraold??αvt?vt?=βvt?1?+(1?β)gradt?
其
中
α
为
学
习
率
,
β
是
超
参
数
,
g
r
a
d
t
是
第
t
才
的
梯
度
。
α
往
往
会
比
我
们
在
传
统
梯
度
下
降
时
指
定
的
学
习
率
更
低
。
其中\alpha为学习率,\beta是超参数,grad_t是第t才的梯度。\\\alpha往往会比我们在传统梯度下降时指定的学习率更低。
其中α为学习率,β是超参数,gradt?是第t才的梯度。α往往会比我们在传统梯度下降时指定的学习率更低。
# GRADED FUNCTION: update_parameters_with_momentum
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
Update parameters using Momentum
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- python dictionary containing the current velocity:
v['dW' + str(l)] = ...
v['db' + str(l)] = ...
beta -- the momentum hyperparameter, scalar
learning_rate -- the learning rate, scalar
Returns:
parameters -- python dictionary containing your updated parameters
v -- python dictionary containing your updated velocities
"""
L = len(parameters) // 2 # number of layers in the neural networks
# Momentum update for each parameter
for l in range(1, L + 1):
# (approx. 4 lines)
# compute velocities
# v["dW" + str(l)] = ...
# v["db" + str(l)] = ...
# update parameters
# parameters["W" + str(l)] = ...
# parameters["b" + str(l)] = ...
# YOUR CODE STARTS HERE
v['dW'+str(l)] = beta*v['dW'+str(l)] + (1-beta)*grads['dW'+str(l)]
v['db'+str(l)] = beta*v['db'+str(l)] +(1-beta)*grads['db'+str(l)]
parameters['W'+str(l)] = parameters['W'+str(l)]-learning_rate*v['dW'+str(l)]
parameters['b'+str(l)] = parameters['b'+str(l)]-learning_rate*v['db'+str(l)]
# YOUR CODE ENDS HERE
return parameters, v
RMSprop(Root mean sqare propagate)
相比于直接使用速度代替梯度进行计算,RMSprop采用一种类似累计均方的方法。
第
t
次
迭
代
:
S
0
=
0
S
1
=
β
S
0
+
(
1
?
β
)
g
r
a
d
1
2
.
.
.
S
t
=
β
S
t
?
1
+
(
1
?
β
)
g
r
a
d
t
2
p
a
r
a
n
e
w
=
p
a
r
a
o
l
d
?
α
g
r
a
d
S
t
+
?
第t次迭代:\\ S_0 = 0\\S_1 = \beta S_0 + (1-\beta )grad^2_1\\...\\S_t = \beta S_{t-1} + (1-\beta)grad^2_t\\para_{new} = para_{old} -\alpha \frac{grad}{\sqrt{S_t + \epsilon}}
第t次迭代:S0?=0S1?=βS0?+(1?β)grad12?...St?=βSt?1?+(1?β)gradt2?paranew?=paraold??αSt?+??grad?
事实上RMSprop用处相比于Momentum和Adam,范围和用途都比较少。
Adam
Adam的方法相当于上述两个方法的结合体,同时使用了v和s。
第
t
次
迭
代
:
v
t
=
β
1
v
t
?
1
+
(
1
?
β
1
)
g
r
a
d
t
v
t
c
o
r
r
e
c
t
e
d
=
v
t
1
?
β
1
t
S
t
=
β
2
S
t
?
1
+
(
1
?
β
2
)
g
r
a
d
t
S
t
c
o
r
r
e
c
t
d
=
S
t
1
?
β
2
t
p
a
r
a
n
e
w
=
p
a
r
a
o
l
d
?
α
v
t
c
o
r
r
e
c
t
d
S
t
c
o
r
r
e
t
e
d
第t次迭代:\\ v_t = \beta_1 v_{t-1}+(1-\beta_1)grad_t\\ v_t^{corrected} = \frac{v_t}{1-\beta_1^t}\\ \\S_t = \beta_2 S_{t-1} + (1-\beta_2)grad_t\\ \\S_t^{correctd} = \frac{S_t}{1-\beta_2^t}\\ \\para_{new} = para_{old} - \alpha \frac{v_t^{correctd}}{S_t^{correted}}
第t次迭代:vt?=β1?vt?1?+(1?β1?)gradt?vtcorrected?=1?β1t?vt??St?=β2?St?1?+(1?β2?)gradt?Stcorrectd?=1?β2t?St??paranew?=paraold??αStcorreted?vtcorrectd??
# GRADED FUNCTION: update_parameters_with_adam
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
"""
Update parameters using Adam
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
t -- Adam variable, counts the number of taken steps
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates
beta2 -- Exponential decay hyperparameter for the second moment estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
Returns:
parameters -- python dictionary containing your updated parameters
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""
L = len(parameters) // 2 # number of layers in the neural networks
v_corrected = {} # Initializing first moment estimate, python dictionary
s_corrected = {} # Initializing second moment estimate, python dictionary
# Perform Adam update on all parameters
for l in range(1, L + 1):
# Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
# (approx. 2 lines)
# v["dW" + str(l)] = ...
# v["db" + str(l)] = ...
# YOUR CODE STARTS HERE
v['dW'+str(l)] = beta1*v['dW'+str(l)]+(1-beta1)*grads['dW'+str(l)]
v['db'+str(l)] = beta1*v['db'+str(l)]+(1-beta1)*grads['db'+str(l)]
# YOUR CODE ENDS HERE
# Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
# (approx. 2 lines)
# v_corrected["dW" + str(l)] = ...
# v_corrected["db" + str(l)] = ...
# YOUR CODE STARTS HERE
v_corrected['dW'+str(l)]=v['dW'+str(l)]/(1-beta1**t)
v_corrected['db'+str(l)]=v['db'+str(l)]/(1-beta1**t)
# YOUR CODE ENDS HERE
# Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
#(approx. 2 lines)
# s["dW" + str(l)] = ...
# s["db" + str(l)] = ...
# YOUR CODE STARTS HERE
s['dW'+str(l)]=beta2*s['dW'+str(l)]+(1-beta2)*grads['dW'+str(l)]**2
s['db'+str(l)]=beta2*s['db'+str(l)]+(1-beta2)*grads['db'+str(l)]**2
# YOUR CODE ENDS HERE
# Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
# (approx. 2 lines)
# s_corrected["dW" + str(l)] = ...
# s_corrected["db" + str(l)] = ...
# YOUR CODE STARTS HERE
s_corrected['dW'+str(l)]=s['dW'+str(l)]/(1-beta2**t)
s_corrected['db'+str(l)]=s['db'+str(l)]/(1-beta2**t)
# YOUR CODE ENDS HERE
# Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
# (approx. 2 lines)
# parameters["W" + str(l)] = ...
# parameters["b" + str(l)] = ...
# YOUR CODE STARTS HERE
parameters['W'+str(l)]=parameters['W'+str(l)]-learning_rate*v_corrected['dW'+str(l)]/(np.sqrt(s_corrected['dW'+str(l)])+epsilon)
parameters['b'+str(l)]=parameters['b'+str(l)]-learning_rate*v_corrected['db'+str(l)]/(np.sqrt(s_corrected['db'+str(l)])+epsilon)
# YOUR CODE ENDS HERE
return parameters, v, s, v_corrected, s_corrected
上诉的几种优化方法不仅可以加快训练速度,并且还可以一定程度上避免陷入局部最优值(可以想象为一个具有滑雪选手可以冲破一些较小的凹处、山谷,从而达到终点)
学习率下降(Learning Rate Decay)
在算法达到快要最优值得时候,我们会发现优化器会在最优值周围徘徊,因为学习率的设置,我们设置的步长往往太大了,然而初始设置步长很小又会导致速度便面,这个使用我们就可以采用一种很简单的方法使得学习率下降。
α
t
=
f
(
t
)
?
α
0
f
是
一
个
单
调
下
降
的
函
数
\alpha_t = f(t)* \alpha_0\\ \\f是一个单调下降的函数
αt?=f(t)?α0?f是一个单调下降的函数
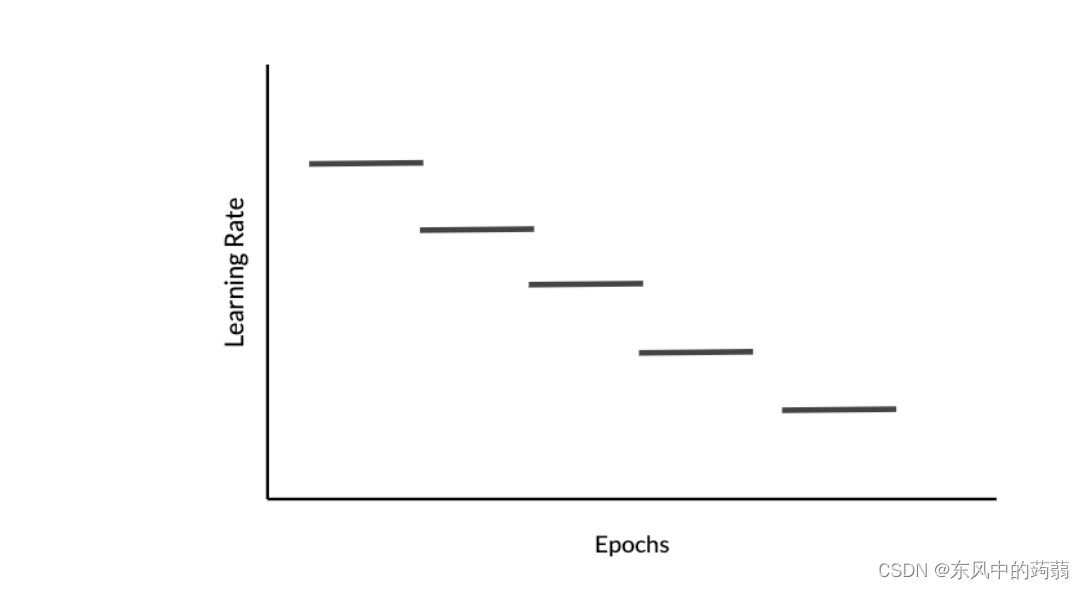
有时为了防止学习率降为0,或者经常更新导致的速度问题,
f
函
数
f函数
f函数常常设置为阶段函数。
α = 1 1 + d e c a y ? [ e p o c h e s t i m e I n t e r v e l ] \alpha =\frac{1}{1+decay*[\frac{epoches}{timeIntervel}]} α=1+decay?[timeIntervelepoches?]1?
几种优化方法的比较
源数据
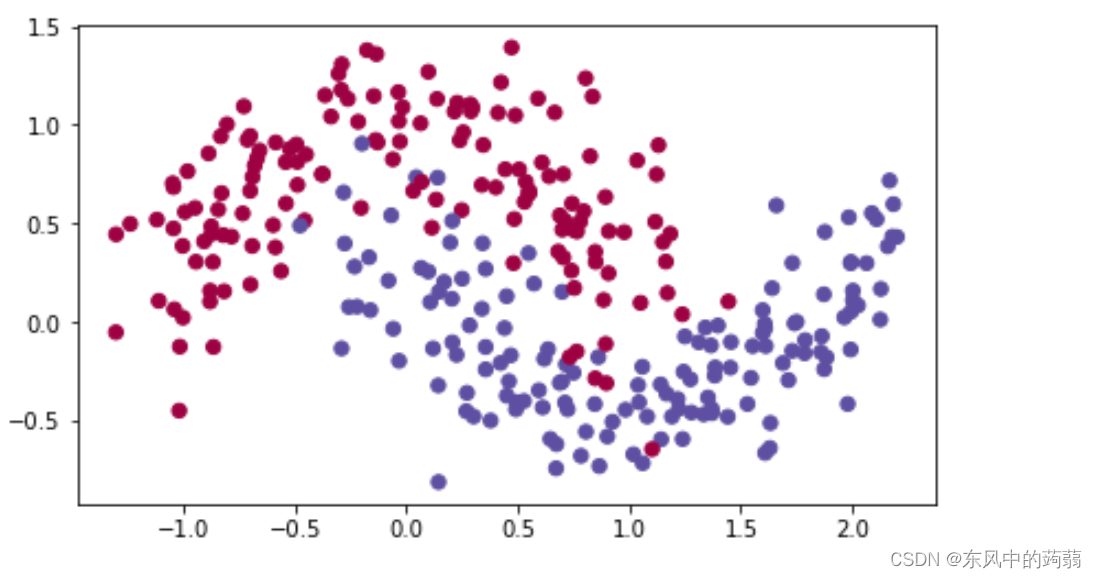
- 带预测数据如上(两个对称的月牙数据)
- 模型使用三层全连接神经网络
- 经过4000次迭代
- mini_batch相同
传统梯度下降

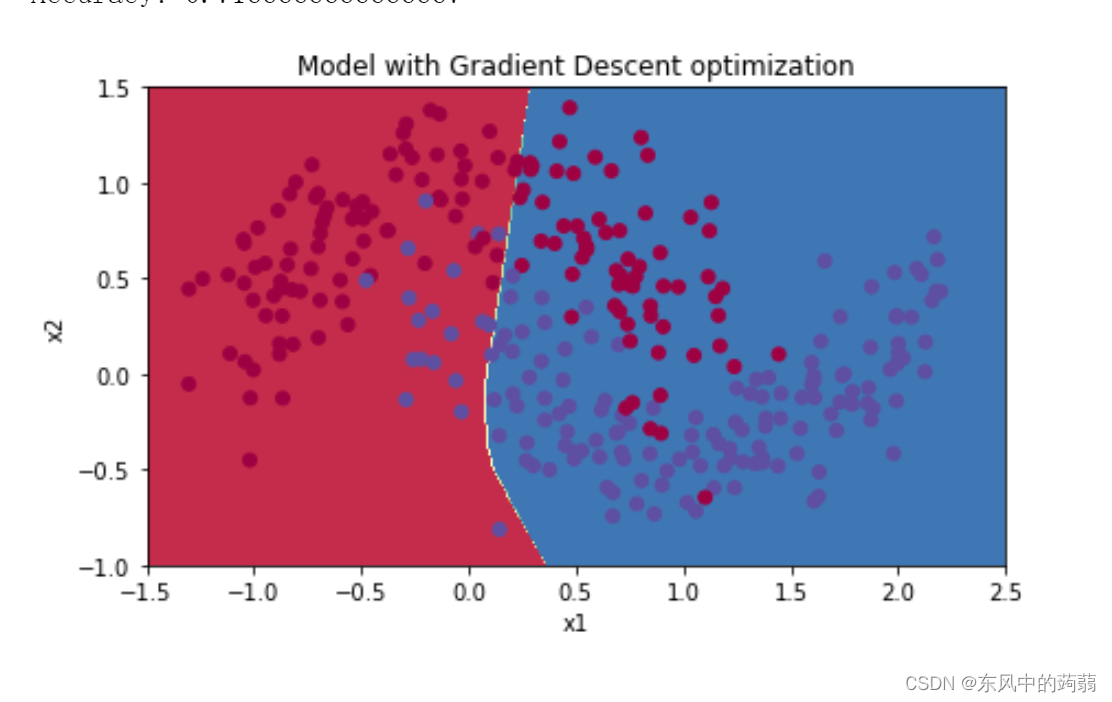
↑
\uparrow
↑传统梯度下降算法
↑
\uparrow
↑
带动量的梯度下降

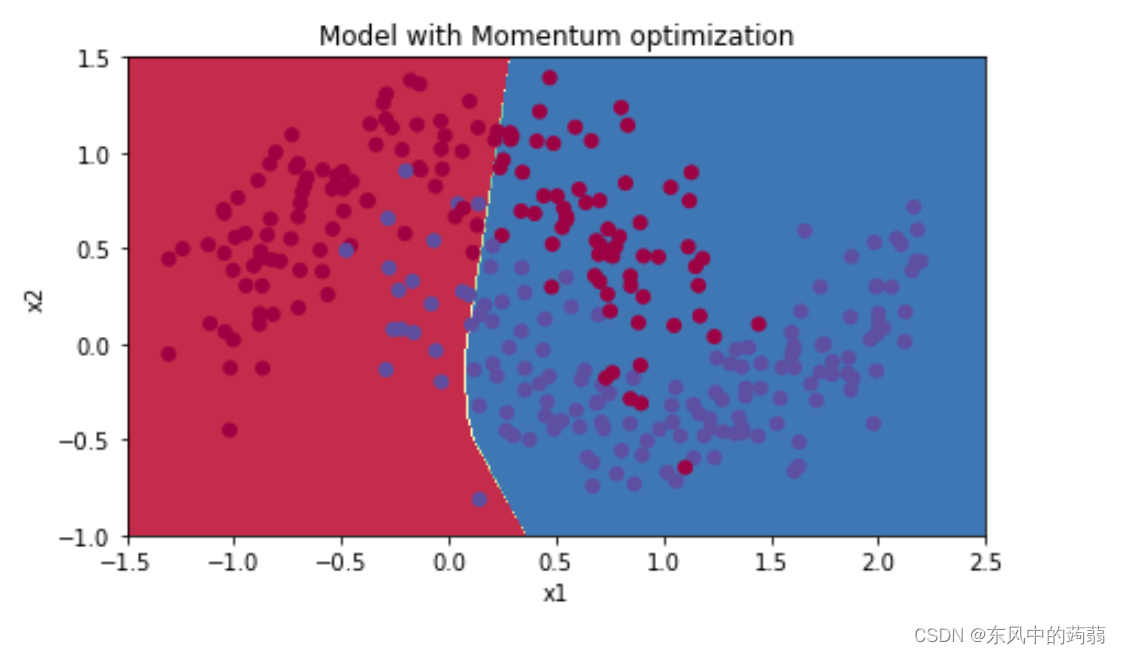
Adam
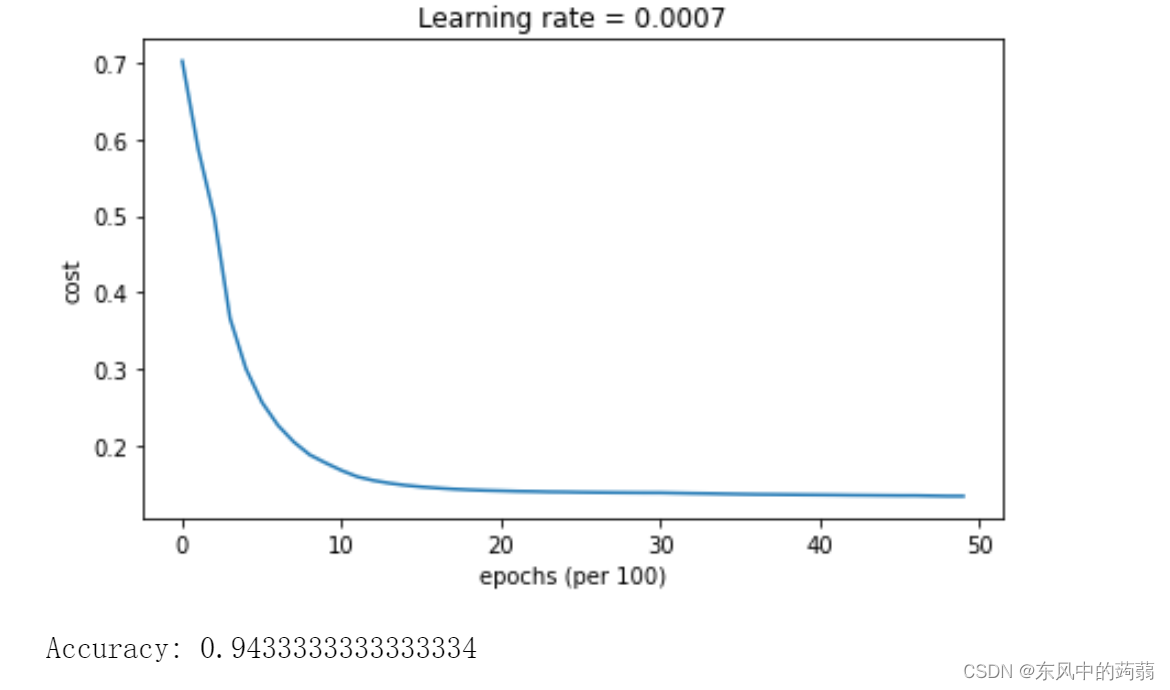
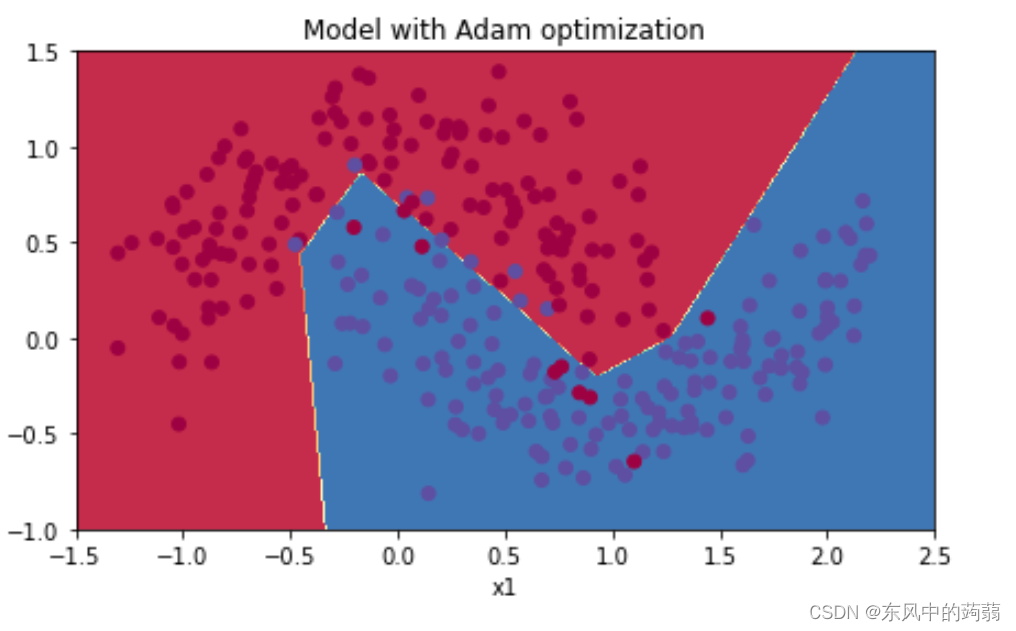
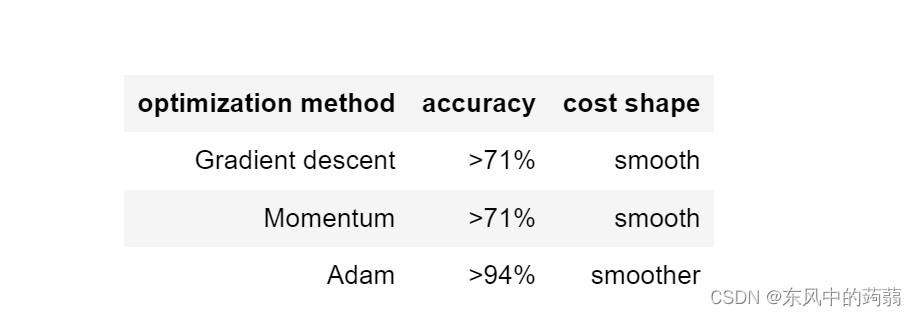
GD+ LearningRate Decay
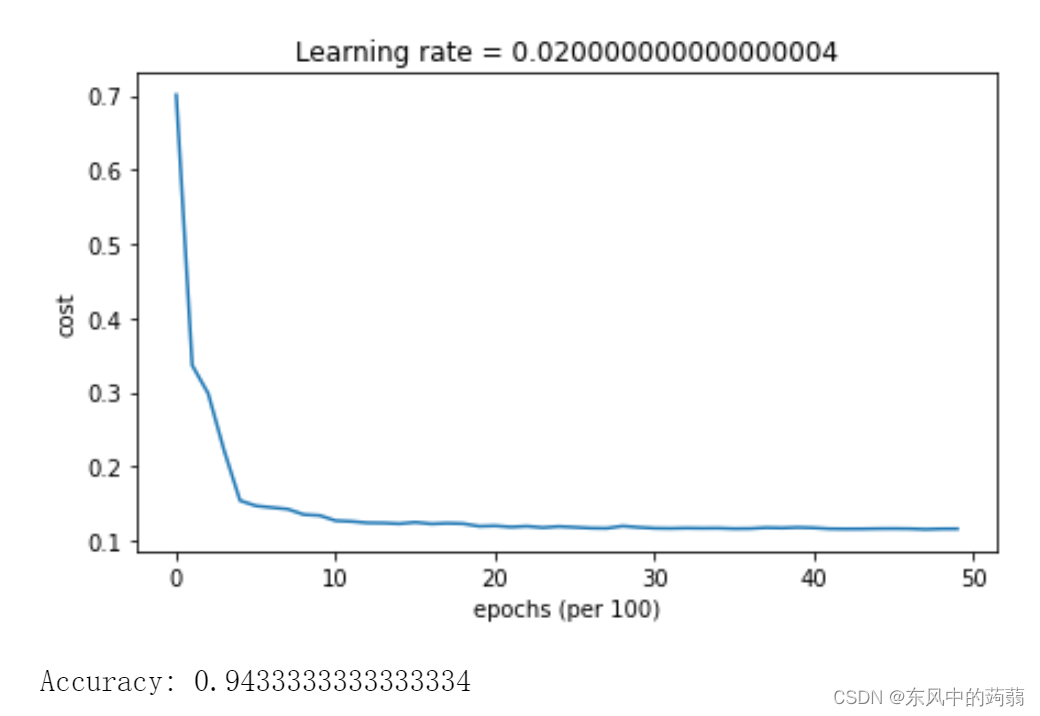
Momentum + LearningRate Decay
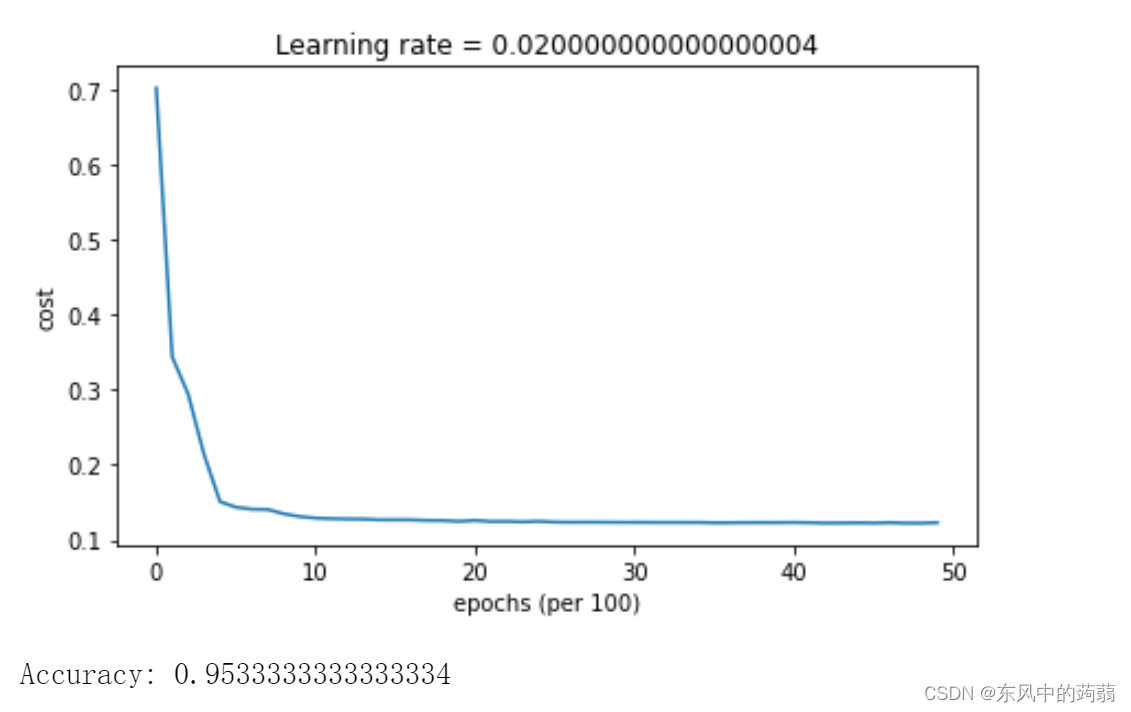
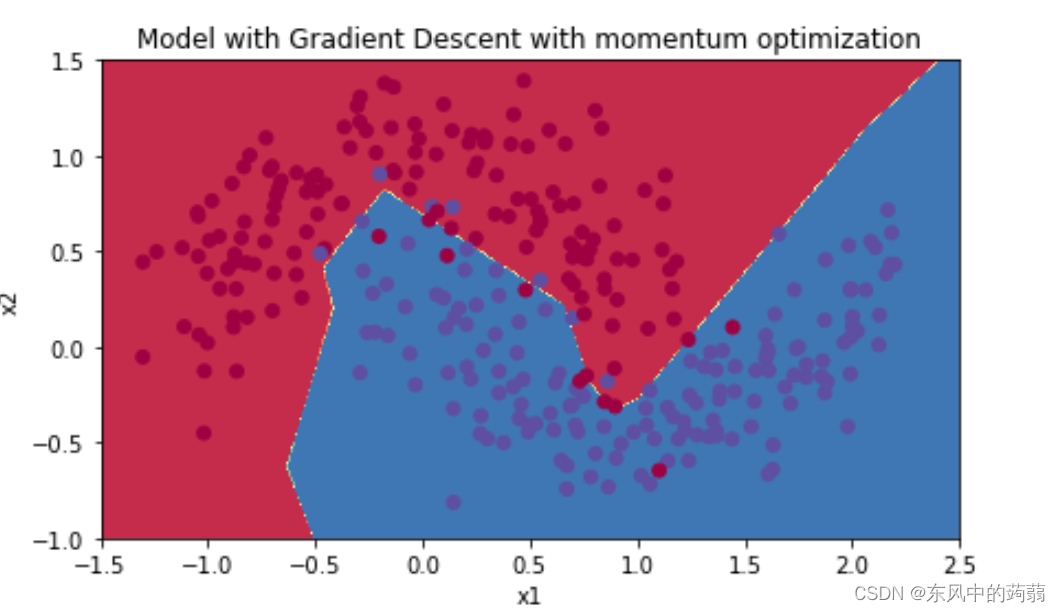
Adam + LearningRate Decay