多目标跟踪(二)DeepSort——级联匹配Matching Cascade
前言
DeepSort算法作为Sort算法的改进,也是现在普遍用的比较多的算法之一,自然也是有很多优越之处,也有很多人对此进行分析学习,但个人认为其中最值得学习的是其提出了,解决处理测量值到跟踪器之间的转换关系且一定程度解决了由于物体被遮挡时间太久,卡尔曼滤波器预测结果发散的问题——级联匹配
本实验还是以YOLOV5为上游检测网络构建的,我自己的代码具体放到下面链接上了,然后整体代码的使用还是比较简单的,写在readme里了,如果有问题请指出。
如果对Sort算法不了解,可以看下面链接。
一、Deepsort与sort之间的区别
在说级联匹配前,先说一下Deepsort相较于sort之间的改进和区别。
跟踪器部分
- 卡尔曼滤波:相对于Sort算法中7个维度的信息,Deepsort中使用了8个维度的信息,分别为目标框中心坐标(u,v),长宽比γ,高h以及这四个变量的一阶导数,表示变换速率。且和Sort中一样,其都定义为一个恒速模型,即后面四个变量都设定为常数。这部分个人认为改动不大,相当将原来的面积部分——改动为检测框的长框比和其中一维高或宽的变化

- 观测状态的定义:在Sort中,当卡尔曼滤波检测到结果,立即会将结果进行跟新,也即去和检测框进行IOU匹配。而在Deepsort中,我们把检测到的结果分为确定态和非确定态,初始时均为非确定态,只有连续3帧的匹配上(这里的匹配,和Sort中的直接IOU匹配类似)才能转为确定态,而转为确定态的预测结果,则会根检测框进行Matching Cascade-级联匹配。这一步的改变,我认为是DeepSort中优越与Sort的重要因素。
指派分配问题
- 代价矩阵的定义:在Sort中,对于代价矩阵,即是直接计算卡尔曼滤波预测出来的结果和检测网络结果的IOU作为代价矩阵。而在DeepSort中,由上面所说的,在非确定态下和Sort类似,都是以IOU为代价矩阵。而在确定态下DeepSort引入了马氏距离和余弦距离。在DeepSort中马氏距离最终用于筛选掉不符合要求的框,而余弦距离才是作为真正的代价矩阵的计算。其中余弦距离计算的不是卡尔曼预测的结果和检测网络的结果,而是计算REID网络作用与前两者之后的结果。REID网络详情等下次再说。

其实Sort和DeepSort实质上就是由这两部分组成的,具体没有说到的细节,可以自己去代码中自己看看。
二、DeepSort中的级联匹配Matching Cascade
根据上面所说的在DeepSort中,对于卡尔曼滤波的结果分为确定态和非确定态,对于确定态的预测结果,才会进行级联匹配。其实整个级联匹配的过程也十分简单。

?在卡尔曼滤波结果中,对于确定态的跟踪框集合我们记为T,当前目标检测出来的结果集合我们记为D。
第一步
我们先将这两者T和D内的结果对应的图像送到REID网络中(我们这里先不管得到的是什么),然后去计算网络计算出来结果的余弦距离,以此作为代价矩阵costmatrix这里记为C。
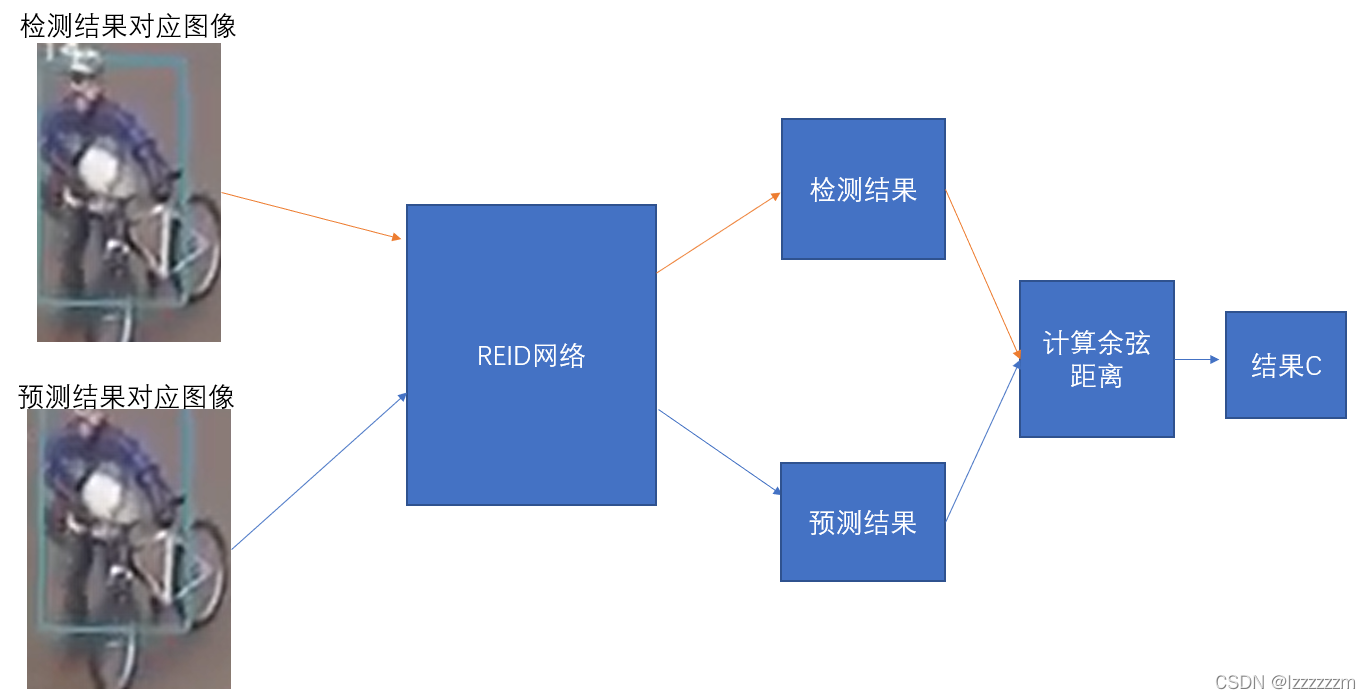
第二步
?我们再去计算检测和预测结果的马氏距离,然后根据统计学和实验所得的阈值,去除掉不符合马氏距离和余弦距离阈值的匹配项。(这里马氏距离仅仅作为去除不符合的匹配项而已)
?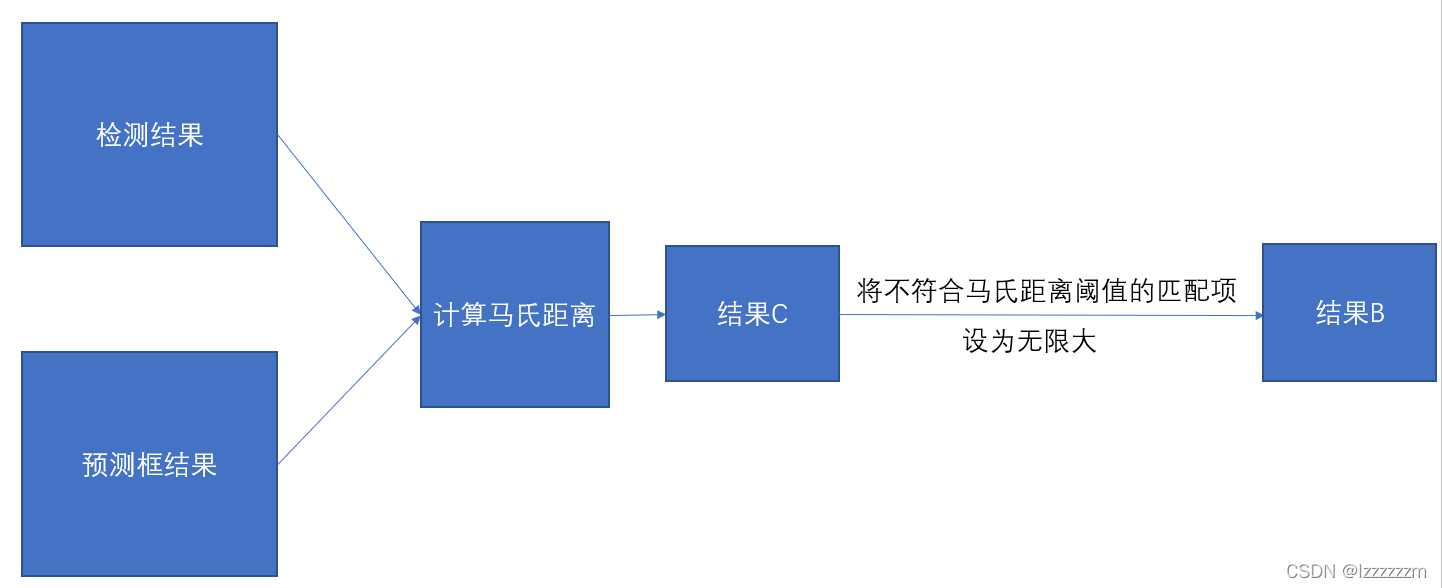
?这里的检测结果为检测框的(x,y,a,h)NX4的形式,预测框结果则为卡尔曼滤波预测出来结果的协方差矩阵8X8,以此去计算的马氏距离。
第三步?
根据预测框的更新状态(这里更新状态是指,这个预测框距离上一次被匹配成功的时间),越新的预测框(也即距离上一次被匹配上的帧数越短的),越优先根据C的结果进行匈牙利算法进行匹配——也即作者认为,越新的框越有可能和当前的检测框匹配上。
最后根据B中的结果去划分匹配上的集合和未匹配上的集合。
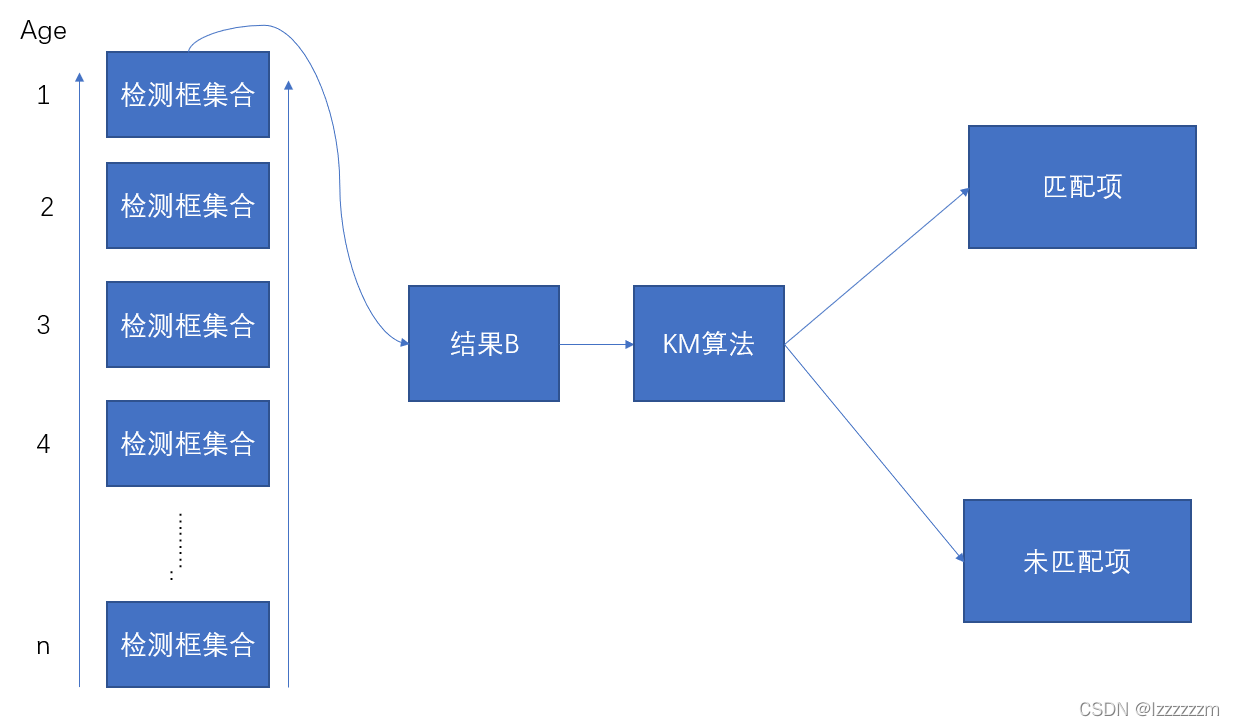
级联匹配其实十分简单,概况起来其实就上面的三步,但他却十分有效的解决了Sort中IDSW的问题,一部分归功于DeepSort中引入REID网络来提取行人特征,另一部分就是在提出了级联匹配这个算法。
级联匹配算法,相对于提升了每个预测器的寿命,不至于只要检测不到就会被删除。
总结
当然,网上关于DeepSort文章一搜一大把,而且也十分详细,而本人认为其中比较值得学习的两部分,一部分是本文的级联匹配,另一部分则是一个属于另一个领域的REID网络。
而且虽然说,DeepSort有着不错的效果,但放到今天,也有更多更优秀的算法与网络替代且值得学习。