Leslie 模型
模型基本
前面介绍了 Malthus 和 Logistic 两种预测人口数(或者说生物数量:草履虫、微生物)的模型,今天接着讲 Leslie 矩阵模型。
虽然前面的预测都是从问题的数据出发,通过数据之间的联系得出拟合出预测方程,简单的很;但是由于只需要较少的数据可以得到方程,往往精度比较低(尽管可以通过调整拟合所需的数据多少来提升精度,但还是有限)。如果需要考虑到种群间 (以人为例) 的年龄结构,那么前面两种模型便不是这么适合,虽然人口总数可以通过原先的两种模型用总的增长率直接求出,但是不同年龄段的人的增长率是不一样的,所以如果想提高人口总数预测的准确率,则不妨考虑不同年龄段的 “繁殖率” 和 “死亡率” 。
由 Leslie 在20世纪40年代用向量形式的差分方程 Leslie (莱斯利)矩阵模型描述女性人口变化规律。
百度百科:Leslie 矩阵模型利用某一初始时刻种群的年龄分布,动态预测种群年龄分布随时间的演变过程。这是一个线性的种群数量动力学模型,通过 Leslie 矩阵可以得出,当时间充分时,种群的年龄分布趋于稳定,总数量趋于指数增长、指数衰变,或保持不变。
模型构建
现以考虑女性人口数量为例:
假设女性的最大年龄为 s 岁,将 s 岁分成 n 组,即 n 个年龄区间,其中
Δ
i
=
[
(
i
?
1
)
s
n
,
i
s
n
]
,
i
=
1
,
2
,
…
…
,
n
\Delta_{i} = [ \frac{(i-1)s}{n},\frac{is}{n}] , i = 1,2,……,n
Δi?=[n(i?1)s?,nis?],i=1,2,……,n
为第
i
i
i 组所属的年龄区间,设第
i
i
i 组的女性在
t
k
t_{k}
tk? 时的人数为
x
i
k
(
i
=
1
,
2
,
…
…
,
n
)
x^{k}_{i} (i=1,2,……,n)
xik?(i=1,2,……,n),则女性人口年龄分布向量为
x
k
=
(
x
1
k
,
x
2
k
,
…
…
,
x
n
k
)
T
x^{k}=(x^{k}_{1},x^{k}_{2},……,x^{k}_{n})^{T}
xk=(x1k?,x2k?,……,xnk?)T
易知,
x
x
x 随时间
t
t
t 变化,不妨考虑每隔
s
n
\frac{s}{n}
ns? 年观察一次,不考虑同一时间间隔内的变化(将时间离散化)。设初始时间为
t
0
t_{0}
t0? ,则
t
k
=
t
0
+
k
s
n
t_{k} = t_{0}+k\frac{s}{n}
tk?=t0?+kns?;假设只考虑自然生育、衰老和死亡引起的人口变化(不考虑其它天灾人祸,难测量的变量),设第
i
i
i 组女性的生育率为
a
i
a_{i}
ai? (第
i
i
i 组女性在
s
n
\frac{s}{n}
ns? 年生育的女婴数,男婴不考虑,
a
i
≥
0
a_{i}\geq 0
ai?≥0),存活率为
b
i
b_{i}
bi? (第
i
i
i 组女性在
s
n
\frac{s}{n}
ns? 年依旧活着的人数与原来人数之比,
0
≤
b
i
≤
1
0\leq b_{i}\leq1
0≤bi?≤1),则死亡率可以表示为
1
?
b
i
1-b_{i}
1?bi? ,这些数据一般可以通过查找相应资料获得也可以通过其它预测方法得到,比如时间序列预测。
当
t
=
t
k
t = t_{k}
t=tk? 时,第1组女性(女婴)是
t
k
?
1
t_{k-1}
tk?1? 时由各组女性生育的,所以其数量可以表示为:
x
1
k
=
a
1
x
1
k
?
1
+
a
2
x
2
k
?
1
+
…
…
+
a
n
x
n
k
?
1
x^{k}_{1} = a_{1}x^{k-1}_{1}+a_{2}x^{k-1}_{2}+……+a_{n}x^{k-1}_{n}
x1k?=a1?x1k?1?+a2?x2k?1?+……+an?xnk?1?
第
i
i
i 组
(
i
≥
2
)
(i \geq 2)
(i≥2) 的女性是
t
k
?
1
t_{k-1}
tk?1? 时刻由第
i
?
1
i-1
i?1 组女性经过
s
n
\frac{s}{n}
ns? 年存活下来的,可以表示为:
x
i
k
=
b
i
?
1
x
i
?
1
k
?
1
(
i
≥
2
)
x^{k}_{i} = b_{i-1}x^{k-1}_{i-1} \qquad(i \geq 2)
xik?=bi?1?xi?1k?1?(i≥2)
用矩阵表示:
[
x
1
k
x
2
k
x
3
k
?
x
n
k
]
=
[
a
1
a
2
?
a
n
?
1
a
n
b
1
0
?
0
0
0
b
2
?
0
0
?
?
?
?
?
0
0
?
b
n
?
1
0
]
[
x
1
k
?
1
x
2
k
?
1
x
3
k
?
1
?
x
n
k
?
1
]
\left[ \begin{matrix} x^{k}_{1} \\ x^{k}_{2} \\ x^{k}_{3} \\ \vdots \\ x^{k}_{n} \\ \end{matrix} \right]= \left[ \begin{matrix} a_{1} & a_{2} & \cdots & a_{n-1} & a_{n} \\ b_{1} & 0 & \cdots & 0 & 0 \\ 0 & b_{2} & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & b_{n-1} & 0 \\ \end{matrix} \right] \left[ \begin{matrix} x^{k-1}_{1} \\ x^{k-1}_{2} \\ x^{k-1}_{3} \\ \vdots \\ x^{k-1}_{n} \\ \end{matrix} \right]
????????x1k?x2k?x3k??xnk??????????=????????a1?b1?0?0?a2?0b2??0???????an?1?00?bn?1??an?00?0?????????????????x1k?1?x2k?1?x3k?1??xnk?1??????????
记
L
=
[
a
1
a
2
?
a
n
?
1
a
n
b
1
0
?
0
0
0
b
2
?
0
0
?
?
?
?
?
0
0
?
b
n
?
1
0
]
x
(
k
)
=
[
x
1
k
x
2
k
x
3
k
?
x
n
k
]
L = \left[ \begin{matrix} a_{1} & a_{2} & \cdots & a_{n-1} & a_{n} \\ b_{1} & 0 & \cdots & 0 & 0 \\ 0 & b_{2} & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & b_{n-1} & 0 \\ \end{matrix} \right] \qquad x^{(k)} = \left[ \begin{matrix} x^{k}_{1} \\ x^{k}_{2} \\ x^{k}_{3} \\ \vdots \\ x^{k}_{n} \\ \end{matrix} \right]
L=????????a1?b1?0?0?a2?0b2??0???????an?1?00?bn?1??an?00?0?????????x(k)=????????x1k?x2k?x3k??xnk??????????
其中
L
L
L 就是 Leslie 矩阵;由于年龄结构相对稳定,所以
L
L
L 一般不会随
t
t
t 变化,则得到
x
(
k
)
=
L
k
x
(
0
)
x^{(k)} = L^{k}x^{(0)}
x(k)=Lkx(0) 可以看出
L
L
L 与马尔可夫中的转移概率矩阵有些相似。
运用上式就可以预测出
t
k
t_{k}
tk? 时刻各个年龄段的人口数。通过 Leslie 模型我们可以发现,在自然情况下,当时间无穷大时,人口增长率和年龄分布结构都会趋于一个稳定状态,而这又与 Leslie 矩阵的特征值和特征向量有关。
矩阵有唯一的单重正特征值
λ
1
\lambda_{1}
λ1? (这里不详细证明),对应的特征向量为:
v
1
=
(
1
,
b
1
λ
1
,
b
1
b
2
λ
1
2
,
?
,
b
1
b
2
?
b
n
?
1
λ
1
n
?
1
)
T
v_{1} = (1,\frac{b_{1}}{\lambda_{1}}, \frac{b_{1}b_{2}}{\lambda^{2}_{1}},\cdots, \frac{b_{1}b_{2}\cdots b_{n-1}}{\lambda^{n-1}_{1}})^{T}
v1?=(1,λ1?b1??,λ12?b1?b2??,?,λ1n?1?b1?b2??bn?1??)T
如果
λ
1
\lambda_{1}
λ1? 是 Leslie 矩阵的正特征值,则该矩阵的任一特征值
λ
\lambda
λ 都会满足:
∣
λ
∣
≤
λ
1
|\lambda| \leq \lambda_{1}
∣λ∣≤λ1?
若 Leslie 矩阵的第一行有两个顺序元素
a
i
,
a
i
+
1
>
0
a_{i},a_{i+1} > 0
ai?,ai+1?>0 ,则该矩阵的正特征值是严格优势特征值,容易证明,该条件在人口模型中是成立的。
若矩阵有严格优势特征值
λ
1
\lambda_{1}
λ1? ,且其特征向量为
x
1
x_{1}
x1? ,则有
lim
?
k
→
+
∞
x
k
λ
1
k
=
c
v
1
\lim_{k\rightarrow +\infty} \frac{x^{k}}{\lambda^{k}_{1}}= cv_{1}
k→+∞lim?λ1k?xk?=cv1?
即当时间无穷大时,年龄分布结构趋于稳定状态,各年龄段的人数占总人数的比例趋于
v
1
v_{1}
v1? 中各部分在总的占比。而人口增长率趋于
λ
1
?
1
\lambda_{1}-1
λ1??1 ,若
λ
1
>
1
\lambda_{1} > 1
λ1?>1,则表明人口增长(二胎政策),若
λ
1
<
1
\lambda_{1} < 1
λ1?<1,则表明人口减少(计划生育),若
λ
1
=
1
\lambda_{1} = 1
λ1?=1,则表明人口稳定。
模型改进
当把男性也考虑进去时, Leslie 矩阵就变为如下形式:
L
=
[
a
1
a
2
?
a
n
?
1
a
n
0
0
?
0
0
b
1
0
?
0
0
0
0
?
0
0
0
b
2
?
0
0
0
0
?
0
0
?
?
?
?
?
?
?
?
?
?
0
0
?
b
n
?
1
0
0
0
?
0
0
a
1
?
a
2
?
?
a
n
?
1
?
a
n
?
0
0
?
0
0
0
0
?
0
0
b
1
?
0
?
0
0
0
0
?
0
0
0
b
2
?
?
0
0
?
?
?
?
?
?
?
?
?
?
0
0
?
0
0
0
0
?
b
n
?
1
?
0
]
L = \left[ \begin{matrix} a_{1} & a_{2} & \cdots & a_{n-1} & a_{n} \quad & 0 & 0 & \cdots & 0 & 0 \\ b_{1} & 0 & \cdots & 0 & 0 \quad & 0 & 0 & \cdots & 0 & 0 \\ 0 & b_{2} & \cdots & 0 & 0 \quad & 0 & 0 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots& \vdots \quad& \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & b_{n-1} & 0 \quad & 0 & 0 & \cdots & 0 & 0 \\ \\a^{*}_{1} & a^{*}_{2} & \cdots & a^{*}_{n-1} & a^{*}_{n} \quad & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cdots & 0 & 0 \quad & b^{*}_{1} & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cdots & 0 & 0 \quad & 0 & b^{*}_{2} & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \quad & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 0 & 0 \quad & 0 & 0 & \cdots & b^{*}_{n-1} & 0 \\ \end{matrix} \right]
L=?????????????????????a1?b1?0?0a1??00?0?a2?0b2??0a2??00?0????????????an?1?00?bn?1?an?1??00?0?an?00?0an??00?0?000?00b1??0?0?000?000b2???0????????????000?0000?bn?1???000?0000?0??????????????????????
其中左上角的矩阵依旧是原来的女性 Leslie 矩阵,而左下角的 a ? a^{*} a? 是女性生育出男婴的生殖率,而右下角的 b ? b^{*} b? 是各年龄段男性的存活率。
相关例题
例1:
某种动物的最大年龄为 6 岁,以两年为一个年龄段进行观测,2010年观测各个年龄段的数量、生育率、存活率如下表所示,预测2018年该动物的各年龄段的数量及分布比例、总数的增长率。
| 年龄 | [0,2) | [2,4) | [4,6) |
|---|---|---|---|
| 数量 | 160 | 320 | 80 |
| 生育率 | 0 | 4 | 3 |
| 存活率 | 0.5 | 0.25 | 0 |
clear;clc;
% 构建 Leslie 矩阵
L = zeros(3,3);
L(1,2) = 4; L(1,3) = 3; % 生育率
L(2,1) = 0.5; L(3,2) = 0.25; % 存活率
x0 = [160,320,80]'; % 初始数量
x = L^((2018-2010)/2)*x0 % 8年后的数量
d = x/sum(x) % 各年龄段数量占比
r = (sum(x)-sum(x0))/sum(x0) % 8年总增长率
计算结果如下:

例2:
用如下加拿大1965年的统计资料研究加拿大的人口年龄结构
| 年龄组i | 年龄区间 | 生育率 | 存活率 |
|---|---|---|---|
| 1 | [0,5) | 0.00000 | 0.99651 |
| 2 | [5,10) | 0.00024 | 0.99820 |
| 3 | [10,15) | 0.05861 | 0.99802 |
| 4 | [15,20) | 0.28608 | 0.99729 |
| 5 | [20,25) | 0.44791 | 0.99694 |
| 6 | [25,30) | 0.36399 | 0.99621 |
| 7 | [30,35) | 0.22259 | 0.99460 |
| 8 | [35,40) | 0.10459 | 0.99184 |
| 9 | [40,45) | 0.02826 | 0.98700 |
| 10 | [45,50) | 0.00240 | - |
clear;clc;
% 构建 Leslie 矩阵
L = zeros(10,10);
% 生育率
L(1,2) = 0.00024; L(1,3) = 0.05861; L(1,4) = 0.28608; L(1,5) = 0.44791;
L(1,6) = 0.36399; L(1,7) = 0.22259; L(1,8) = 0.10459; L(1,9) = 0.02826; L(1,10) = 0.00240;
% 存活率
L(2,1) = 0.99651; L(3,2) = 0.99820; L(4,3) = 0.99802; L(5,4) = 0.99729;
L(6,5) = 0.99694; L(7,6) = 0.99621; L(8,7) = 0.99460; L(9,8) = 0.99184; L(10,9) = 0.98700;
[v,d] = eig(L); % 计算 Leslie 矩阵的特征向量v和特征值d
lambda_1 = d(1,1) % 唯一的单重正特征值
v_1 = v(:,1); % 对应特征值的特征向量
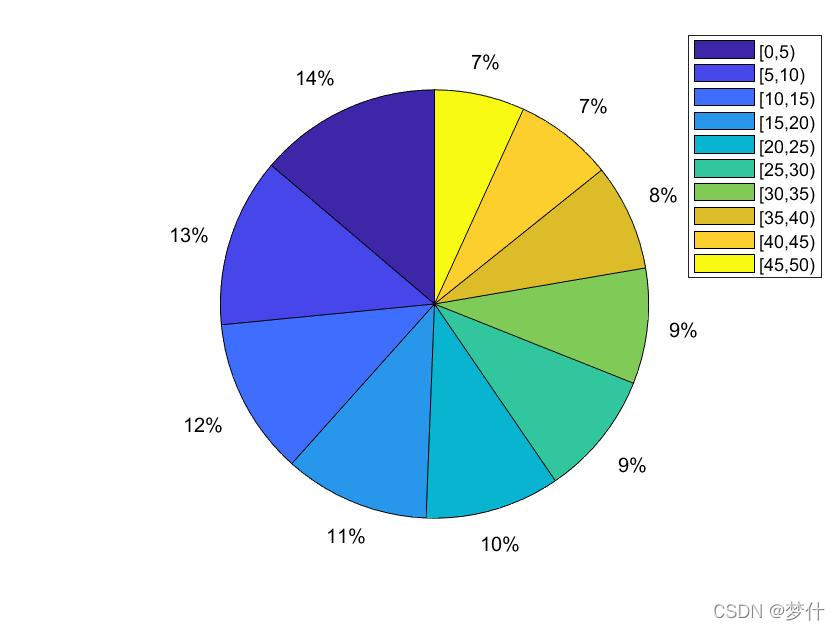
v_bar = v(:,1)/sum(v(:,1)); % 年龄分布向量
pie(v_bar)
legend('[0,5)','[5,10)','[10,15)','[15,20)','[20,25)','[25,30)','[30,35)','[35,40)','[40,45)','[45,50)')
由 Leslie 矩阵的性质可知,当时间无穷大时,年龄分布趋于稳定,可用单重正特征向量求出。结果如下:
灵敏度分析
从模型可以看出, λ 1 \lambda_{1} λ1? 是关键参数,而 λ 1 \lambda_{1} λ1? 的大小和 Leslie 矩阵有关,也就是和生育率 a a a 和 存活率 b b b 有关,当 a a a 和 b b b 改变时, λ 1 \lambda_{1} λ1? 也会发生变化,所以可以构建相关的方程来辨别模型的灵敏度,看模型是否稳定,若 λ 1 > 1 \lambda_{1} > 1 λ1?>1,则表明种群趋于增大,若 λ 1 < 1 \lambda_{1} < 1 λ1?<1,则表明种群趋于灭亡,若 λ 1 = 1 \lambda_{1} = 1 λ1?=1,则表明种群相对稳定。
该模型在预测生物群落方面有很大的作用,如遇到相关问题可以试着用该模型求解。
美赛题目涉及:
ICM 2000 B 题:大象种群稳定发展
MCM 2007 A 题:中国人口增长预测
参考
《数学建模竞赛入门与提高》周凯,宋军全,邬学军
任强,侯大道.人口预测的随机方法:基于Leslie矩阵和ARMA模型[J].人口研究,2011,35(02):28-42.
陈克伟.Leslie矩阵模型的参数灵敏度分析[J].北京师范大学学报(自然科学版),1986(02):1-3.