[人工智能]机器学习日记（9）

机器学习日记（9）

支持向量机(Support Vector Machines)

优化目标(Optimization Objective)

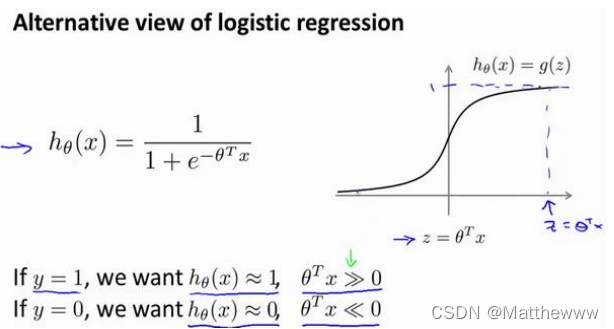
在逻辑回归中我们已经熟悉了这里的假设函数形式，和右边的S型激励函数。然而，为了解释一些数学知识,将用𝑧 表示𝜃^𝑇𝑥。
现在考虑下我们想要逻辑回归做什么：如果有一个 𝑦 = 1的样本，不管是在训练集中或是在测试集中，又或者在交叉验证集中，总之是 𝑦 = 1，现在我们希望?_𝜃(𝑥) 趋近1。因为我们想要正确地将此样本分类，这就意味着当 ?_𝜃(𝑥)趋近于 1 时，𝜃^𝑇𝑥 应当远大于 0，这里的>>意思是远远大于 0。这是因为由于 𝑧 表示 𝜃^𝑇𝑥，当 𝑧远大于 0 时，即到了该图的右边，你不难发现此时逻辑回归的输出将趋近于 1。相反地，如果我们有另一个样本，即𝑦 = 0。我们希望假设函数的输出值将趋近于 0，这对应于𝜃^𝑇𝑥，或者就是 𝑧 会远小于 0，因为对应的假设函数的输出值趋近 0。

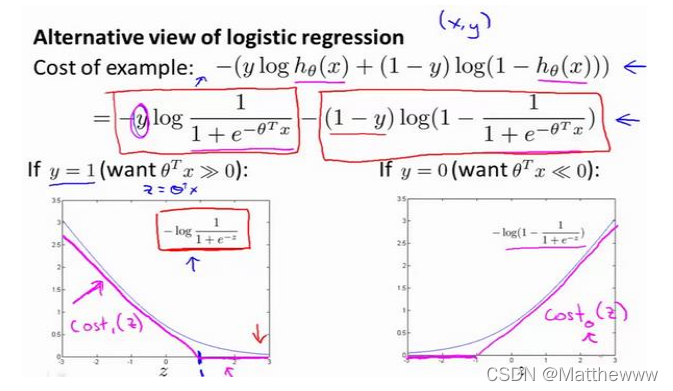
如果进一步观察逻辑回归的代价函数，会发现每个样本 (𝑥, 𝑦)都会为总代价函数，增加这里的一项，因此，对于总代价函数通常会有对所有的训练样本求和，并且这里还有一个1/𝑚项，但是，在逻辑回归中，这里的这一项就是表示一个训练样本所对应的表达式。现在，如果我将完整定义的假设函数代入这里。那么，我们就会得到每一个训练样本都影响这一项。现在先忽略 1/𝑚 这一项，但是这一项是影响整个总代价函数的。
考虑两种情况：一种是𝑦等于 1 的情况；另一种是 𝑦 等于 0 的情况。
在第一种情况中，假设 𝑦 = 1 ，此时在目标函数中只需有第一项起作用，因为𝑦 = 1时，(1 ? 𝑦)项将等于 0。因此，当在 𝑦 = 1 的样本中时，即在 (𝑥, 𝑦)中 ，我们得到 𝑦 = ?log(1 ? 1/1+𝑒^?𝑧)这样一项，其中 𝑧 表示𝜃^𝑇𝑥，即： 𝑧 = 𝜃^𝑇𝑥。当然，在代价函数中，𝑦 前面有负号。我们只是这样表示，如果 𝑦 = 1 代价函数中，这一项也等于 1。这样做是为了简化此处的表达式。如果画出关于𝑧 的函数，你会看到左下角的这条曲线，我们同样可以看到，当𝑧 增大时，也就是相当于𝜃^𝑇𝑥增大时，𝑧 对应的值会变的非常小。对整个代价函数而言，影响也非常小。这也就解释了，为什么逻辑回归在观察到正样本𝑦 = 1时，试图将𝜃^𝑇𝑥设置得非常大。因为，在代价函数中的这一项会变的非常小。
现在开始建立支持向量机，我们从这里开始：
在𝑦 = 1的前提下，我们会从代价函数的第一项开始，也就是?log(1 ? 1/1+𝑒^?𝑧)一点一点修改，让我取这里的𝑧 = 1点，画出将要用的代价函数。
新的代价函数是由两条线段组成，即位于右边的水平部分和位于左边的直线部分，且不需过多的考虑左边直线部分的斜率，这能为支持向量机带来计算上的优势。例如，更容易计算股票交易的问题等等。
另外一种情况是𝑦 = 0，当𝑦 = 0时，代价函数只留下了第二项，因此，这个样本的代价或是代价函数的贡献。将会由这一项表示。并且，如果将这一项作为𝑧的函数，那么，这里就会得到横轴𝑧。现在，完成了支持向量机中的部分内容，用相似的方法替代这一条蓝色的线。
如果我们用一个新的代价函数来代替，即这条从 0 点开始的水平直线，然后是一条斜
线，像上述两图。第一张图的函数称之为cos𝑡₁ (𝑧)，第二张图函数我称它为cos𝑡₀(𝑧)。这里的下标是指在代价函数中，对应的 𝑦 = 1 和 𝑦 = 0 的情况，拥有了这些定义后，现在，我们就开始构建支持向量机

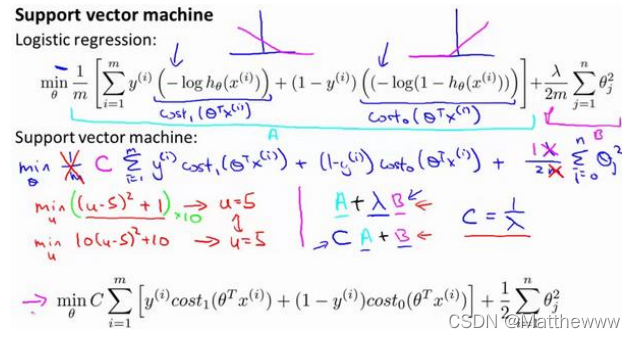
这是我们在逻辑回归中使用代价函数𝐽(𝜃)。也许这个方程看起来不是非常熟悉。这是因为之前有个负号在方程外面，但是，这里所做的是，将负号移到了表达式的里面，这样做使得方程看起来有些不同。对于支持向量机而言，实质上我们要将这替换为cos𝑡₁(𝑧)，也就是cos𝑡₁(𝜃^𝑇𝑥)，同样地，我也将这一项替换为cos𝑡₀(𝑧)，也就是代价cos𝑡₀(𝜃^𝑇𝑥)。因此，对于支持向量机，我们得到了这里的最小化问题，即:

然后，再加上正则化参数。现在，按照支持向量机的惯例，事实上，我们的书写会稍微有些不同，代价函数的参数表示也会稍微有些不同。
首先，我们要除去1/𝑚这一项，当然，这仅仅是由于人们使用支持向量机时，对比于逻辑回归而言，不同的习惯所致，但这里我所说的意思是：你知道，我将要做的是仅仅除去1/𝑚这一项，但是，这也会得出同样的 𝜃 最优值，好的，因为1/𝑚 仅是个常量，因此，你知道在这个最小化问题中，无论前面是否有1/𝑚 这一项，最终我所得到的最优值𝜃都是一样的。这里我的意思是，先给你举一个实例，假定有一最小化问题：即要求当(𝑢 ? 5)2 + 1取得最小值时的𝑢值，这时：当𝑢 = 5时取得最小值。现在，如果我们想要将这个目标函数乘上常数 10，这里我的最小化问题就变成了：求使得10 × (𝑢 ? 5)2 + 10最小的值𝑢，然而，使得这里最小的𝑢值仍为 5。因此将一些常数乘以你的最小化项，这并不会改变最小化该方程时得到𝑢值。因此，这里所做的是删去常量𝑚。也相同的，将目标函数乘上一个常量𝑚，并不会改变取得最小值时的𝜃值。
第二点是概念上的变化，我们只是指在使用支持向量机时，一些如下的标准惯例，而不是
逻辑回归。因此，对于逻辑回归，在目标函数中，我们有两项：第一个是训练样本的代价，
第二个是我们的正则化项，我们不得不去用这一项来平衡。这就相当于我们想要最小化𝐴加
上正则化参数𝜆，然后乘以其他项𝐵对吧？这里的𝐴表示这里的第一项，同时我用 B 表示第二
项，但不包括𝜆，我们不是优化这里的𝐴 + 𝜆 × 𝐵。我们所做的是通过设置不同正则参数𝜆达
到优化目的。这样，我们就能够权衡对应的项，是使得训练样本拟合的更好。即最小化𝐴。
还是保证正则参数足够小，也即是对于 B 项而言，但对于支持向量机，按照惯例，我们将使
用一个不同的参数替换这里使用的𝜆来权衡这两项。你知道，就是第一项和第二项我们依照
惯例使用一个不同的参数称为𝐶，同时改为优化目标，𝐶 × 𝐴 + 𝐵因此，在逻辑回归中，如果
给定𝜆，一个非常大的值，意味着给予 B 更大的权重。而这里，就对应于将𝐶 设定为非常小
的值，那么，相应的将会给𝐵比给𝐴更大的权重。因此，这只是一种不同的方式来控制这种
权衡或者一种不同的方法，即用参数来决定是更关心第一项的优化，还是更关心第二项的优
化。当然你也可以把这里的参数𝐶 考虑成1/𝜆，同 1/𝜆所扮演的角色相同，并且这两个方程
或这两个表达式并不相同，因为𝐶 = 1/𝜆，但是也并不全是这样，如果当𝐶 = 1/𝜆时，这两个
优化目标应当得到相同的值，相同的最优值 𝜃。因此，就用它们来代替。那么，我现在删掉
这里的𝜆，并且用常数𝐶来代替。因此，这就得到了在支持向量机中我们的整个优化目标函
数。然后最小化这个目标函数，得到 SVM 学习到的参数𝐶。

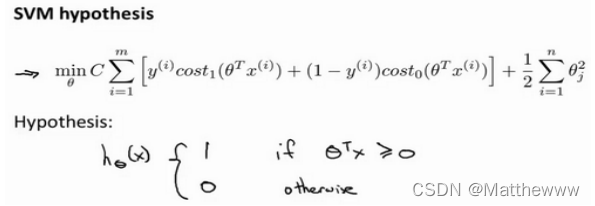
最后有别于逻辑回归输出的概率。在这里，我们的代价函数，当最小化代价函数，获得参数𝜃时，支持向量机所做的是它来直接预测𝑦的值等于 1，还是等于 0。因此，这个假设函数会预测 1。当𝜃𝑇𝑥大于或者等于 0 时，或者等于 0 时，所以学习参数𝜃就是支持向量机假设函数的形式。那么，这就是支持向量机数学上的定义。

大边界的直观理解（Large Margin Intuition）

人们有时将支持向量机看作是大间距分类器

这是支持向量机模型的代价函数，在左边画出了关于𝑧的代价函数cos𝑡₁(𝑧)，此函数用于正样本，而在右边画出了关于𝑧的代价函数cos𝑡₀(𝑧)，横轴表示𝑧，现在考虑一下，最小化这些代价函数的必要条件是什么。如果你有一个正样本，𝑦 = 1，则只有在𝑧 >= 1时，代价函cos𝑡₁(𝑧)才等于 0。换句话说，如果你有一个正样本，我们会希望𝜃^𝑇𝑥>=1，反之，如果𝑦 = 0，我们观察一下，函数cos𝑡₀(𝑧)，它只有在𝑧 <= ?1的区间里函数值为 0。这是支持向量机的一个有趣性质。事实上，如果你有一个正样本𝑦 = 1，则其实我们仅仅要求𝜃𝑇𝑥大于等于 0，就能将该样本恰当分出，这是因为如果𝜃^𝑇𝑥>0 大的话，我们的模型代价函数值为 0，类似地，如果你有一个负样本，则仅需𝜃^𝑇𝑥<=0 就会将负例正确分离，但是，支持向量机的要求更高，不仅仅要能正确分开输入的样本，即不仅仅要求𝜃^𝑇𝑥>0，我们需要的是比 0 值大很多，比如大于等于 1，我也想这个比 0 小很多，比如我希望它小于等于-1，这就相当于在支持向量机中嵌入了一个额外的安全因子，或者说安全的间距因子。
当然，逻辑回归做了类似的事情。但是让我们看一下，在支持向量机中，这个因子会导致什么结果。具体而言，我接下来会考虑一个特例。我们将这个常数𝐶设置成一个非常大的值。比如我们假设𝐶的值为 100000 或者其它非常大的数，然后来观察支持向量机会给出什么结果？

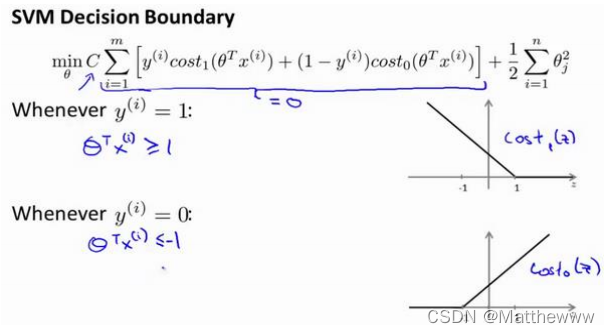
如果𝐶非常大，则最小化代价函数的时候，我们将会很希望找到一个使第一项为0的最优解。因此，让我们尝试在代价项的第一项为0的情形下理解该优化问题。比如我们可以把𝐶设置成了非常大的常数，这将给我们一些关于支持向量机模型的直观感受。

我们已经看到输入一个训练样本标签为𝑦 = 1，你想令第一项为 0，你需要做的是找到
一个𝜃，使得𝜃^𝑇𝑥 >= 1，类似地，对于一个训练样本，标签为𝑦 = 0，为了使cos𝑡₀(𝑧) 函数的
值为 0，我们需要𝜃^𝑇𝑥 <= ?1。因此，现在考虑我们的优化问题。选择参数，使得第一项等
于 0，就会导致下面的优化问题，因为我们将选择参数使第一项为 0，因为这个函数的第一
项为 0，所以是𝐶乘以 0 加上二分之一乘以第二项。这里第一项是𝐶乘以 0，可以将其删
去。
这将遵从以下的约束：𝜃^𝑇𝑥(𝑖) >= 1，如果 𝑦(𝑖)是等于 1 的，𝜃^𝑇𝑥(𝑖) <= ?1，如果样本𝑖是一个负样本，这样当你求解这个优化问题的时候，最小化这个关于变量𝜃的函数时，会得到一个非常有趣的决策边界

具体而言，考察这样一个数据集，其中有正样本，也有负样本，可以看到这个数据集是线性可分的。存在多条不同的直线，可以把正样本和负样本完全分开。

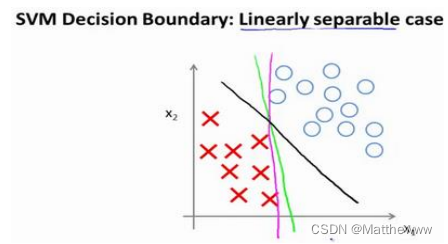
比如，一个近乎垂直决策边界（粉色）可以把正样本和负样本分开。但是多多少少看起来并不非常自然，或者我们可以画一条更差的决策界（绿色），这是另一条决策边界，可以将正样本和负样本分开，但仅仅是勉强分开，这些决策边界看起来都不是特别好的选择，支持向量机将会选择这个黑色的决策边界，相较于之前我用粉色或者绿色画的决策界。这条黑色的看起来好得多，黑线看起来是更稳健的决策界。在分离正样本和负样本上它显得的更好。数学上来讲，这是什么意思呢？这条黑线有更大的距离，这个距离叫做间距(margin)。

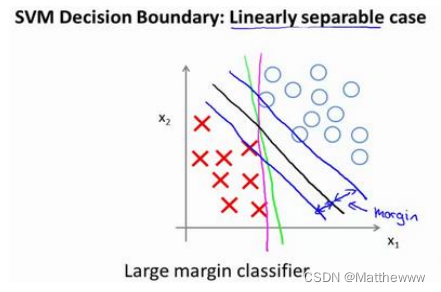
当画出这两条额外的蓝线，我们看到黑色的决策界和训练样本之间有更大的最短距离。然而粉线和蓝线离训练样本就非常近，在分离样本的时候就会比黑线表现差。因此，这个距离叫做支持向量机的间距，而这是支持向量机具有鲁棒性的原因，因为它努力用一个最大间距来分离样本。因此支持向量机有时被称为大间距分类器，而这其实是求解优化问题的结果，，即支持向量机模型的做法，即努力将正样本和负样本用最大的间距分开。
最后一点：我们将这个大间距分类器中的正则化因子常数𝐶设置的非常大，在这将其设置为了100000，因此对这样的一个数据集，也许我们将选择这样的决策界，从而最大间距地分离开正样本和负样本。那么在让代价函数最小化的过程中，我们希望找出在𝑦 = 1和𝑦 = 0两种情况下都使得代价函数中左边的这一项尽量为零的参数。如果我们找到了这样的参数，则我们的最小化问题便转变成：

事实上，支持向量机现在要比这个大间距分类器所体现得更成熟，尤其是当使用大间
距分类器的时候，学习算法会受异常点(outlier) 的影响。比如我们加入一个额外的正样
本。

在这里，当加了这个样本时，为了将样本用最大间距分开，也许最终会得到一条类似于粉色的决界，仅仅基于一个异常值，仅仅基于一个样本，就将决策界从这条黑线变到这条粉线，这实在是不明智的。而如果正则化参数𝐶设置的非常大，这事实上正是支持向量机将会做的。它将决策界从黑线变到了粉线，但是如果𝐶设置的小一点，则最终会得到这条黑线，当然数据如果不是线性可分的，如果你在这里有一些正样本或者你在这里有一些负样本，则支持向量机也会将它们恰当分开。因此，大间距分类器的描述，仅仅是从直观上给出了正则化参数𝐶非常大的情形，同时提醒𝐶的作用类似于1/𝜆，𝜆是我们之前使用过的正则化参数。这只是𝐶非常大的情形，或者等价地 𝜆 非常小的情形。你最终会得到类似粉线这样的决策界，但是实际上应用支持向量机的时候，当𝐶不是非常非常大的时候，它可以忽略掉一些异常点的影响，得到更好的决策界。甚至当你的数据不是线性可分的时候，支持向量机也可以给出好的结果。

核函数（Kernels）

可以使用高级数的多项式模型来解决无法用直线进行分隔的分类问题：

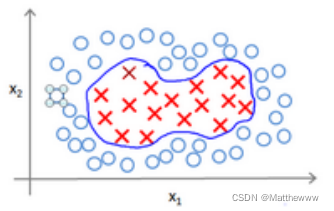
为了获得上图所示的判定边界，我们的模型可能是𝜃₀ + 𝜃₁𝑥₁ + 𝜃₂𝑥₂ + 𝜃₃𝑥₁𝑥₂ + 𝜃₄𝑥₁² + 𝜃₅𝑥₂² + ?的形式。我们可以用一系列的新的特征 f 来替换模型中的每一项。例如令： 𝑓₁ = 𝑥₁, 𝑓₂ = 𝑥₂, 𝑓₃ = 𝑥₁𝑥₂, 𝑓4 = 𝑥₁², 𝑓₅ = 𝑥₂²
…得到?_𝜃(𝑥) = 𝜃₁𝑓₁ + 𝜃₂𝑓₂+. . . +𝜃_𝑛𝑓_𝑛。然而，除了对原有的特征进行组合以外，有没有更好的方法来构造𝑓1, 𝑓2, 𝑓3？我们可以利用核函数来计算出新的特征。给定一个训练实例 𝑥 ，我们利用 𝑥 的各个特征与我们预先选定的地标(landmarks)𝑙⁽¹⁾, 𝑙⁽²⁾, 𝑙⁽³⁾的近似程度来选取新的特征𝑓₁, 𝑓₂, 𝑓₃
例如：

其中：

为实例𝑥中所有特征与地标𝑙(1)之间的距离的和。上例中的𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦(𝑥, 𝑙(1))就是核函数，具体而言，这里是一个高斯核函数(Gaussian Kernel)。注：这个函数与正态分布没什么实际上的关系，只是看上去像而已。
这些地标的作用是什么？如果一个训练实例𝑥与地标𝐿之间的距离近似于 0，则新特征𝑓近似于𝑒^?0= 1，如果训练实例𝑥与地标𝐿之间距离较远，则𝑓近似于𝑒^{?(一个较大的数)} = 0。
假设我们的训练实例含有两个特征[𝑥₁ 𝑥₂]，给定地标𝑙(1)与不同的𝜎值，见下图：

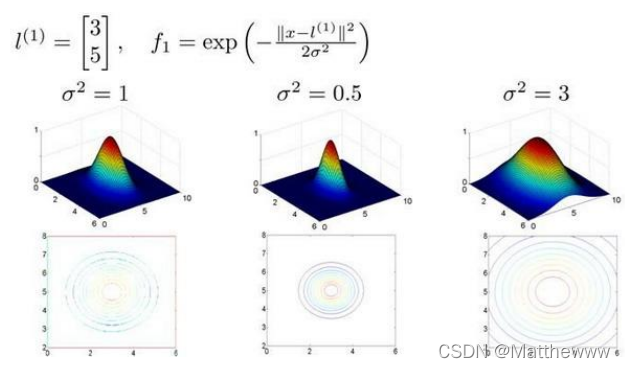
图中水平面的坐标为 𝑥₁，𝑥₂而垂直坐标轴代表𝑓。可以看出，只有当𝑥与𝑙(1)重合时𝑓才
具有最大值。随着𝑥的改变𝑓值改变的速率受到𝜎2的控制。在下图中，当实例处于洋红色的点位置处，因为其离𝑙(1)更近，但是离𝑙(2)和𝑙(3)较远，因此𝑓1接近 1，而𝑓2,𝑓3接近 0。因此?𝜃(𝑥) = 𝜃0 + 𝜃1𝑓1 + 𝜃2𝑓2 + 𝜃1𝑓3 > 0，因此预测𝑦 = 1。同理可以求出，对于离𝑙(2)较近的绿色点，也预测𝑦 = 1，但是对于蓝绿色的点，因为其离三个地标都较远，预测𝑦 = 0。

这样，图中红色的封闭曲线所表示的范围，便是我们依据一个单一的训练实例和我们选取的地标所得出的判定边界，在预测时，我们采用的特征不是训练实例本身的特征，而是通过核函数计算出的新特征𝑓₁, 𝑓₂, 𝑓₃
在上面，我们讨论了核函数，以及怎样利用它去实现支持向量机的一些新特性。现在面临着一个新问题：如何选择地标？
我们通常是根据训练集的数量选择地标的数量，即如果训练集中有𝑚个实例，则我们选
取𝑚个地标，并且令:𝑙⁽¹⁾^ = 𝑥⁽¹⁾, 𝑙⁽²⁾ = 𝑥⁽²⁾, . . . . . , 𝑙^(𝑚) = 𝑥^(𝑚)。这样做的好处在于：现在我们
得到的新特征是建立在原有特征与训练集中所有其他特征之间距离的基础之上的，即：


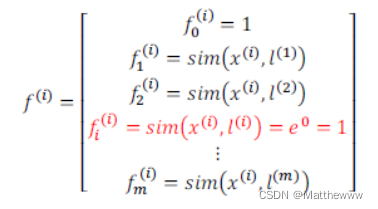
下面我们将核函数运用到支持向量机中，修改我们的支持向量机假设为：
给定𝑥，计算新特征𝑓，当𝜃^𝑇𝑓 >= 0 时，预测 𝑦 = 1，否则反之。
相应地修改代价函数为：


在具体实施过程中，我们还需要对最后的正则化项进行些微调整，在计算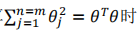
时，我们用𝜃^𝑇𝑀𝜃代替𝜃^𝑇𝜃，其中𝑀是根据我们选择的核函数而不同的一个矩阵。这样做的原因是为了简化计算。理论上讲，我们也可以在逻辑回归中使用核函数，但是上面使用 𝑀来简化计算的方法
不适用与逻辑回归，因此计算将非常耗费时间。
在此，我们不介绍最小化支持向量机的代价函数的方法，你可以使用现有的软件包（如liblinear,libsvm 等）。在使用这些软件包最小化我们的代价函数之前，我们通常需要编写核函数，并且如果我们使用高斯核函数，那么在使用之前进行特征缩放是非常必要的。另外，支持向量机也可以不使用核函数，不使用核函数又称为线性核函数(linear kernel)，当我们不采用非常复杂的函数，或者我们的训练集特征非常多而实例非常少的时候，可以采用这种不带核函数的支持向量机。
下面是支持向量机的两个参数𝐶和𝜎的影响：
𝐶 = 1/𝜆 𝐶 较大时，相当于𝜆较小，可能会导致过拟合，高方差；
𝐶 较小时，相当于𝜆较大，可能会导致低拟合，高偏差；
𝜎较大时，可能会导致低方差，高偏差；
𝜎较小时，可能会导致低偏差，高方差。