[人工智能]【小样本学习】【CVPR2021】补全原型网络达到SOTA，Prototype Completion with Primitive Knowledge for Few-Shot Learning

摘要

小样本学习是一种通过少量样本训练分类器的方法，目前是一项比较困难的任务。目前比较有效的方法是基于元学习的预训练方法，首先在样本比较丰富的基础类别上训练一个特征提取器，然后在样本比较少的新类别上进行微调。然而实验表明微调对网络在新类别上的分类准确率的改进比较有限，本文发现，在用于预训练的基础类别数据集中，每个类别中样本的分布都比较紧凑，不同类别之间泾渭分明，而在样本比较少的新类别数据集中，各个类别中的样本分布比较混乱，不同类别的样本混在一起，不容易分开，即方差比较大。针对上述问题，该文对所有类别的类别词条进行处理，通过WordNet获得其属性词条，将所有类别词条与属性词条经GloVe计算得到词嵌入向量（即对英文单词进行数字化得到高维向量），补全单纯通过样本均值计算得到的原型，提出一种更加具有代表性的类别原型，然后将原始的原型与补全的原型进行高斯融合，得到最终的原型，在新类别数据集上进行N-way K-shot方式的元训练。5-way 1-shot训练后，模型在MiniImageNet的测试集上达到目前最高的73.13%分类准确率。

方法

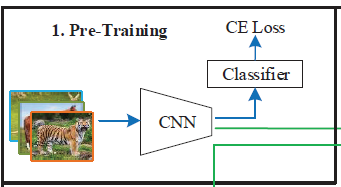
1. 预训练（Pre-Training)
在基础类别$C_{base}$数据集上，使用所有图像样本，以传统的梯度下降训练方法，使用比较大的batch_size（如128）、合适的学习率（如0.001）与学习率衰减策略、合适的优化器（如随机梯度下降，SGD），合适的损失函数（如交叉熵损失函数，CrossEntropyLoss，CE Loss），训练一个卷积神经网络（如ResNet-12），即骨干网络（backbone），训练完成后，删除网络中的所有全连接层（即下图中的Classifier），形成特征提取器$f_{{\theta }_f}$，${\theta }_f$表示特征提取器的所有参数。对该网络输入一张训练图像样本，即可输出样本的特征图，每个batch中的所有图像样本的特征图是多个空间分辨率较低，通道数很多的三维张量， 例如设置batch_size为128，则网络最终输出128个7x7x512的三维张量，可以形象理解为有512张7x7的矩阵沿第三维度叠起来形成一个长方体，这样的长方体有128个。

2. 学习如何补全原型（Learning to Complete Prototypes）
本文提出一种原型补全网络（ProtoComNet）作为元学习器，补全基于每个类别样本均值的原始原型。

1. Step 1
   找到基础类别数据集$D_{base}$中第$k$个类别词条$c_k$的属性词条$a_i$，例如袋鼠（kangaroo）具有长脸和白色腹部，则“长脸（long face）”和“白色腹部（white belly）”就是袋鼠这个类别词条的属性词条，斑马（zebra）也具有长脸，所以斑马的属性词条也包括“长脸“，另外斑马还有四条腿，所以“四条腿（four-footed）”也是斑马的属性词条。
   通过WordNet可以轻松获得MiniImageNet数据集中所有类别词条的属性词条。
   假设基础类别数据集$D_{base}$共含$K$个基础类别$c_k$，通过WordNet获得了所有$K$个基础类别下的$F$个属性词条$a_i$。令集合$A$表示所有属性词条$a_i$的集合，有 A = { a i ∣ i = 1 , 2 , . . . , F } A=\{a_i|i=1,2,...,F\} A={ai?∣i=1,2,...,F}令集合$C_{base}$表示$K$个类别词条$c_k$的集合，即 C b a s e = { c k ∣ k = 1 , 2 , . . . , K } C_{base}=\{c_k|k=1,2,...,K\} Cbase?={ck?∣k=1,2,...,K}令$w_j$表示第$j$个词条，集合$W$表示所有词条$w_j$的集合，有 W = { w j ∣ w j ∈ C b a s e ∪ A , j = 1 , 2 , . . . , K , K + 1 , . . . , K + F } W=\{w_j|w_j\in C_{base}\cup A,j=1,2,...,K,K+1,...,K+F\} W={wj?∣wj?∈Cbase?∪A,j=1,2,...,K,K+1,...,K+F}令$r_{kj}$表示类别词条$c_k$和词条$w_j$之间的关系，有$$r_{kj}=?\begin{array}{ll}1& \text{if?}{w}_j是c_k的属性词条\\ 1& \text{if?}{w}_j=c_k\\ 0& \text{if?otherwise}\end{array}$$令$R$是所有$r_{kj}$的集合，则有$r_{kj}\in R，R\in {\mathbb{R}}^{K\times (K+F)}$。
   使用GloVe算法对词条集合$W$中的所有词条$w_j$数字化，即$h_j=\text{GloVe}(w_j)，$转化成相同长度的词嵌入向量$h_j\in {\mathbb{R}}^{1\times d}$，$d$是向量通道数。令$H$表示所有$h_j$的集合，有 H = { h ? j ∣ j = 1 , 2 , . . . , K + F } , H ∈ R ( K + F ) × d H=\{\vec{h}_j|j=1,2,...,K+F\},H\in \R^{(K+F)\times d} H={h j?∣j=1,2,...,K+F},H∈R(K+F)×d对于MiniImageNet数据集，共$K=100$类别，$F=71$个属性词条，GloVe算法生成$d=300$的词嵌入向量，则 $H$是171x300的矩阵，$R$是171x171的稀疏矩阵。在矩阵$R$中，由于共$K=100$个类别，因此从第101行开始，后面的所有元素都是0，矩阵中0的数量远大于1的数量，从而$R$是一个稀疏矩阵。
   

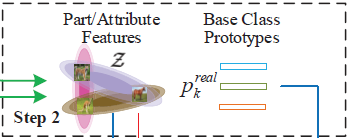
2. Step 2
   在预训练出的特征提取器$f_{{\theta }_f}$和属性词条集合$A$基础上，计算每个基础类别中所有样本特征图的平均值，得到每个基础类别的原型。具体来讲，对于第$k$个基础类别$c_k$，将一张属于$c_k$类别的训练图像样本$x$输入预训练阶段训练好的特征提取器$f_{{\theta }_f}$，得到$x$的特征向量$f_x=f_{{\theta }_f}(x)\in {\mathbb{R}}^{1\times s}$，$s$是特征图通道数，若$f_{{\theta }_f}=\text{ResNet-12}$，则$s=512$。以这种方式计算出$c_k$类别下训练图像样本集合$D_{base}^k$中所有图像的特征向量，求平均值，得到基础类别$c_k$的原型$p_k^{real}$，即$$p_k^{real}=\frac{1}{|D_{base}^k|}\sum _{(x,y)\in D_{base}^k}{f}_{{\theta }_f}(x),p_k^{real}\in {\mathbb{R}}^{1\times s}$$其中$|D_{base}^k|$表示第$k$个类别下训练图像样本的数量。
   对于WordNet提取出的属性词条$a_i$，可以想到这些属性词条也同样属于一些新类别，例如将马作为基础类别，斑马作为新类别，则马的属性词条之一“四条腿”也是斑马的属性词条，即这些属性词条将基础类别和新类别联系了起来。对于第$i$个属性词条$a_i$，找到其所属的所有基础类别，例如对于“四条腿”这一属性词条，马、斑马、大象等类别都具有四条腿，即都含有“四条腿”这一属性词条，然后找出这些类别所包含的所有训练图像样本$x\in D_{base}^{a_i}$。
   接下来计算所有属性词条$a_i$的特征向量$z_{a_i}$（即下图中的Part/Attribute Features）。首先，计算集合$D_{base}^{a_i}$中所有图像样本的均值特征向量${\mu }_{a_i}$和标准差向量${\sigma }_{a_i}$，即$${\mu }_{a_i}=\frac{1}{|D_{base}^{a_i}|}\sum _{(x,y)\in D_{base}^{a_i}}{f}_{{\theta }_f}(x),{\mu }_{a_i}\in {\mathbb{R}}^{1\times s}$$$${\sigma }_{a_i}=\sqrt{\frac{1}{|D_{base}^{a_i}|}\sum _{(x,y)\in D_{base}^{a_i}}{(f_{{\theta }_f}(x)?{\mu }_{a_i})}^2},{\sigma }_{a_i}\in {\mathbb{R}}^{1\times s}$$$$i=1,2,...,F$$其中$|D_{base}^{a_i}|$表示$D_{base}^{a_i}$中样本的数量。其次，以均值特征向量${\mu }_{a_i}$和标准差向量${\sigma }_{a_i}$为参数，构造$s$维正态分布$N({\mu }_{a_i},{\sigma }_{a_i}^2)$（即下图中不同颜色的椭圆形区域。为何使用椭圆形？因为高维正态分布概率密度函数在二维平面上的投影是一个椭圆），从该分布中随机取值，作为属性词条$a_i$的特征向量，即$$z_{a_i}={\mu }_{a_i}+{\sigma }_{a_i}?,z_{a_i}\in {\mathbb{R}}^{1\times s}$$$?$从$s$维标准正态分布中随机取样，$?\in {\mathbb{R}}^{1\times s}$。令$Z$表示所有$z_{a_i}$的集合，有 Z = { z ? a i ∣ a i ∈ A } Z=\{\vec{z}_{a_i}|a_i\in A\} Z={z ai??∣ai?∈A}
   

3. Step 3
   通过Step 1和Step 2，得到了基础类别$c_k$的原型$p_k^{real}$和属性词条$a_i$的特征向量$z_{a_i}$，在这一步中，需要通过原型补全网络（ProtoComNet）$f_{{\theta }_c}$，将集合$R$、集合$H$、集合$Z$和基础类别$c_k$的原型$p_k^{real}$作为输入，输出基础类别$c_k$补全后的原型${\hat{p}}_k$。具体做法如下：
   编码器（Encoder)
   此步需要训练一个输出通道减半的全连接层加ReLU激活函数作为编码器$g_{{\theta }_e}$，即

   self.encoder = nn.Sequential(
       nn.Linear(in_features=s, out_features=s//2),
       nn.ReLU(inplace=True),
   )
   

   在基础类别数据集$D_{base}$中随机选择一个训练图像样本$x$，得到$x$的标签$y$，输入预训练阶段训练好的特征提取器$f_{{\theta }_f}$，即$f_x=f_{{\theta }_f}(x)$，得到$x$的特征向量$f_x\in {\mathbb{R}}^{1\times s}$。对$f_x=(f_1,f_2,...,f_s)$进行线性变换并非线性激活，得到$f_x$的隐编码$b_x=(b_1,b_2,...,b_{s/2})$，即$$b_j=\sum _{i=1}^s{\beta }_{ij}{f}_i+{\gamma }_j$$$$\text{ReLU激活：}{b}_j=\text{max}(0,b_j)$$$$j=1,2,...,\frac{s}{2}$$同样，输入属性词条$a_i$的特征向量$z_{a_i}=(z_1,z_2,...,z_s)$，替换上述式子的$f_i$，计算得到属性词条$a_i$特征向量$z_{a_i}$的隐编码向量$c_{a_i}\in {\mathbb{R}}^{1\times \frac{s}{2}}$

   聚合器（Aggregator）
   不同的属性词条对同一类别具有不同影响，例如属性词条“鼻子”对于“大象”这一类别比“老虎”更有代表性，因此需要构造一种注意力机制达到属性加权目的，此步需要训练一个双层全连接网络作为聚合器$g_{{\theta }_a}$，即

   self.aggregator = nn.Sequential(
               nn.Linear(in_features=d+d+s, out_features=d),
               nn.ReLU(inplace=True),
               nn.Linear(in_features=d, out_features=1)
   

   首先，将训练图像样本$x$的标签$y$对应的类别词嵌入向量$h_y\in {\mathbb{R}}^{1\times d}$、词条$w_m\in W$（$m=1,2,...,K+F$）的词嵌入向量$h_m\in {\mathbb{R}}^{1\times d}$和$x$经过特征提取器$f_{{\theta }_f}$得到的特征向量$f_x\in {\mathbb{R}}^{1\times s}$连接，得到$[h_y||h_m||f_x]\in {\mathbb{R}}^{1\times (d+d+s)}$，对$[h_y||h_m||f_x]$经过上述全连接层，得到隐编码向量$c_x=(c_1,c_2,...,c_{K+F})$，即$$t_{jm}=\sum _{i=1}^{d+d+s}{\delta }_{ij}[h_y||h_m||f_x{]}_i+{\zeta }_j,j=1,2,...,d$$$$t_{jm}=\text{max}(0,t_{jm}),j=1,2,...,d$$$$c_m=\sum _{j=1}^d{\eta }_j{t}_{jm}+\theta$$$$m=1,2,...,K+F$$其次，将隐编码向量$c_x\in {\mathbb{R}}^{1\times (K+F)}$与表示标签$y$对应类别$c_y$对所有词条关系的向量$r_y=(r_1,r_2,...,r_{K+F})$逐元素相乘，即$$\alpha =c_x?r_y,\alpha \in {\mathbb{R}}^{1\times (K+F)},m=1,2,...,K+F$$得到输入$x$时，所有词条的注意力权重$\alpha$。最后，将注意力权重$\alpha =({\alpha }_1,{\alpha }_2,...,{\alpha }_{K+F})$、$x$的特征向量$f_x$经过编码器得到的隐编码向量$b_x=(b_1,b_2,...,b_{\frac{s}{2}})$、集合$Z$中所有属性词条特征向量$z_{a_i}$的隐编码向量$c_i=(c_{i1},c_{i2},...,c_{i\frac{s}{2}})$相乘求和，得到聚合结果$g=(g_1,g_2,...,g_{\frac{s}{2}})$，即$$g_n={\alpha }_y{b}_n+\sum _{i=1}^F{\alpha }_{K+i}{c}_{in},n=1,2,...,\frac{s}{2}$$其中，在注意力权重向量$\alpha$中，由于存在$K$个基础类别，所以前$K$个注意力权重${\alpha }_1,{\alpha }_2,...,{\alpha }_K$是基础类别的注意力权重，后$F$个注意力权重${\alpha }_{K+1},{\alpha }_{K+2},...,{\alpha }_{K+F}$是$F$个属性词条的注意力权重。
   解码器（Decoder）
   解码器$g_{\theta d}$的作用比较简单，只是把向量的维度从$s/2$恢复到$s$，即

   self.decoder = nn.Sequential(
               nn.Linear(in_features=s//2, out_features=512),
               nn.ReLU(inplace=True),
               nn.Linear(in_features=512, out_features=s)
   

   具体公式在此省略，最终得到$x$的标签$y$对应的补全原型${\hat{p}}_y\in {\mathbb{R}}^{1\times s}$。注意，在训练原型补全网络过程中，输入一个训练图像样本$x$，输出一个$x$的标签$y$的补全原型，即在同一基础类别$c_y$中，不同训练图像样本输出的补全原型${\hat{p}}_y$不同。
   训练原型补全网络
   计算Step 2计算得到的基础类别$c_y$的原始原型$p_y^{real}=(p_1^{real},p_2^{real},...,p_s^{real})$和基础类别$c_y$的补全原型${\hat{p}}_y=(p_1,p_2,...,p_s)$之间的均方差损失$E$，即$$E=\frac{1}{s}\sum _{i=1}^s(p_i?p_i^{real}{)}^2$$通过梯度下降方法，以合适的学习率，在降低均方差损失（MSE Loss）$E$的过程中，训练编码器$g_{{\theta }_e}$、聚合器$g_{{\theta }_a}$、解码器$g_{{\theta }_d}$网络的参数和偏置。
   

3. 元训练（Meta-Training）
未完待续