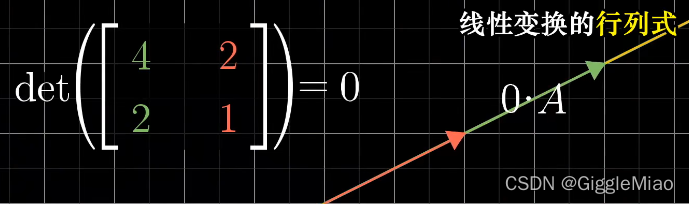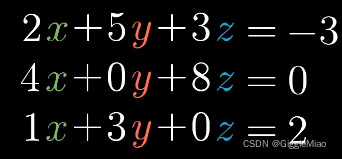[人工智能] 线性代数的本质2

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 线性代数的本质2 -> 正文阅读

[人工智能]线性代数的本质2

干货满满~ 二刷《线性代数的本质》，内容不难，很有助于打开思维。系列文章会尽量把精华都摘下来，有理解不当处欢迎指出。有兴趣的同学也可以直接去刷视频https://www.bilibili.com/video/BV1ys411472E?p=1正在上传…重新上传取消http://linkhttp://link/

行列式

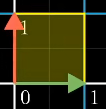
在介绍行列式之前，我们先看一下空间中的变换对向量所围成的面积会带来什么变化，以标准基 $\left ( \hat{i},\hat{j} \right )$ 围成的面积作为单位正方形：

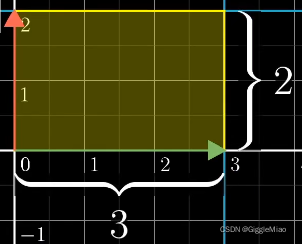
当经过变换 $\begin{bmatrix} 3 &0 \\ 0& 2 \end{bmatrix}$ 后，标准基变化后的向量围成的面积如下：

变换前后基向量围成的面积从1 $\rightarrow$ 6，即扩大了6倍。

这时，就可以引入行列式的概念，特定区域变换改变的面积比例被称为该变换的行列式。

?如：一个线性变换的行列式是3，即将一个区域的面积增加为原来的3倍；一个线性变换的行列式是1/2，即将一个区域的面积缩小一半；特别的，当一个二维线性变换的行列式为0时，说明整个二维平面被压缩成一条线，甚至是一个点上，此时任何区域的面积都变为0。

这里注意噢，高维变低维了，肯定有线性相关的向量了。换句话说，观察一个矩阵代表的变换是否将空间压缩到更小的维度上，只需看该矩阵的行列式是否为0。（行列式为0，存在线性相关，降维啦）

· 对于三维空间来说，行列式表示平行六面体体积的变化比例。

?定向

在我们熟悉的行列式计算中，结果是允许出现负值呢，这该如何解释？

这就需要引入一个定向的概念——如果将二维空间想象成一张纸，若经过某变换后将纸翻转到了另一面，则称类似这样的变换改变了空间的定向。或者用可视化的解释：

1）初始基 $\hat{j}$ 在 $\hat{i}$ 的左侧。

2）变换后 $\hat{i}$ 在 $\hat{j}$ 的左侧，就说明定向发生了改变。

?

· 三维空间中的定向

一般情况下，右手定则可以描述三维空间的方向。伸出右手，右手食指指向 $\hat{i}$ 的方向，中指指向 $\hat{j}$ 的方向，大拇指竖起来指向 $\hat{k}$ 的方向：

如果经过变换之后右手定则仍然成立，则空间定向没有发生改变；如果变换后空间的方向适用于左手定则（下图），则空间的定向发生了改变，结果正负号发生变化。

?注：空间定向的改变虽然会影响行列式结果的正负号，但是行列式的绝对值依然表示区域面积的缩放比例。

逆矩阵、列空间和零空间?

逆矩阵

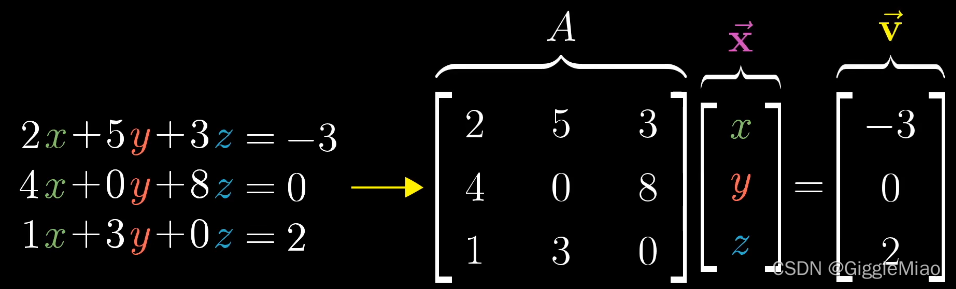
从下面这个方程组的求解进行入手：

?把线性方程组写成矩阵和向量乘积的形式 $A\vec{x}=\vec{v}$ ，表明向量? $\vec{x}$ ?经过变换A之后与向量? $\vec{v}$ ?相同。求解 $A\vec{x}=\vec{v}$ 意味着要去寻找向量 $\vec{x}$ 。

换个思路来求解 $\vec{x}$ ——向量? $\vec{v}$ ?需要经历一个怎样的变换可以变为 $\vec{x}$ ?？这就要求我们对 $\vec{v}$ 进行变换A的逆变换，数学表现形式为矩阵，用 $A^{-1}$ 来表示。

逆变换就是相反的变换，比如A是顺时针旋转90°，则 $A^{-1}$ 就是逆时针旋转90°；那如果写成矩阵相乘的形式 $A^{-1}A$ ，表示先进行A变换，再进行 $A^{-1}$ 变换，就回到了原始状态，相当于没变，即 ${\color{Red} A^{-1}A=E}$ 。

此时，向量 $\vec{x}$ 的求解可以用变换 $A^{-1}$ 实现： $A^{-1}A\vec{x}=A^{-1}\vec{v}$ ，? ?? $\vec{x}=A^{-1}\vec{v}$ ，再对解的情况进行分析：

?1）A的行列式? $\left | A \right |\neq 0$

前面讲到行列式的值代表单位区域面积的缩放比例，当行列式不为0时，说明空间并未被压缩降维，这种情况下A可逆，能找到唯一解 $\vec{x}=A^{-1}\vec{v}$

?2）A的行列式? $\left | A \right |=0$ ?

行列式为0时说明空间被压缩（降维）了，则一个二维向量 $\vec{x}$ 经过变换之后成了一维向量 $\vec{v}$ ，那反过来一维向量是没办法再逆变回二维空间的。所以此时解不唯一确定，可能不存在，可以有无数多个。

秩

?秩表示向量经过变换后空间的维数。当变换的结果为一条直线时，即空间为一维，称该变换的秩为1；当变换后的向量落在某二维平面时，称该变换的秩为2。

列空间

变换后的结果不管是一条直线、二维平面还是三维空间，所有这些可能的变换结果组成的集合，称为矩阵的列空间。矩阵代表变换，矩阵中的列就是标准基变换后的结果，所以也可以说列空间是矩阵的列所张成的空间。

当矩阵的秩达到最大时，意味着秩数与矩阵的列数相等，即满秩。（也说明矩阵中各列向量都是线性无关的）

零空间

当矩阵不是满秩时，说明经过该变换将空间压缩到了一个更低的维度上，由于我们默认向量的起点都在原点，则会有一系列的向量会被压缩为零向量（原点处）。例如一个三维线性变换将空间压缩到二维平面时，会有一整条线上的向量在变换后落在原点零向量上；若一个三维线性变换将空间压缩至一条直线上时，就会有一整个平面上的向量在变换后落在原点。?

?那么，这些由于变换后空间被压缩而落在原点的向量集合，称为矩阵的零空间或“核”。

?对于线性方程组来说，当向量? $\vec{v}$ ?恰好为零向量时? $A\vec{x}=\begin{bmatrix} 0\\ 0 \end{bmatrix}$ ?时，零空间给出的就是这个向量方程组所有可能的解。（原因：当向量? $\vec{v}$ ?恰好为零向量时，说明二维向量? $\vec{x}$ ?经过变换后降成了一维，那些由于空间压缩落在原点的向量都在零空间里。反之，要求解 $\vec{x}$ ，就要把所有被压缩的向量进行复原，即零空间中的所有向量。）

?点积与对偶性

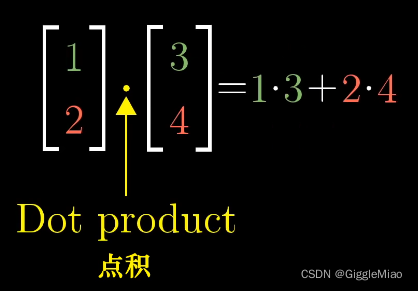
点积

当有两个维数相同的向量时，可以进行点积运算，一般我们是将对应位置的数值相乘再求和得到点积结果：

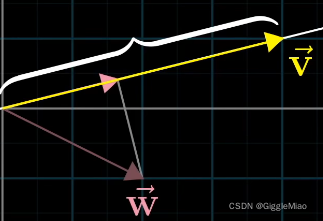
从点积运算背后的几何意义也可以通过向量 $\vec{w}$ 在向量 $\vec{v}$ 上的投影值乘以向量 $\vec{v}$ 的长度得到：

而且利用投影计算时，与顺序是无关的。即将 $\vec{v}$ 投影到 $\vec{w}$ 上，与将 $\vec{w}$ 投影到 $\vec{v}$ 上的结果是一样的：

?

说到投影还牵扯到方向问题：1）当两个向量的方向大致一致的时候，即向量1在向量2上的投影方向与向量2同向，点积的结果带正号；2）当两个向量的方向大致相反的时候，即向量1在向量2上的投影方向与向量2反向，点积的结果带负号；3）当两个向量相互垂直时，即向量1在向量2上的投影为零向量，点积结果为0。

为什么两个向量的点积运算与投影有关系？引入对偶性。

对偶性

在介绍对偶性之前，先讨论一件事——多维空间到一维空间的线性变换。（一维空间在下文中用数轴代替）

说到底，我们还是要看空间中经过了哪些线性变换。老规矩，跟踪基向量的变换情况来分析其他向量的变化。以二维空间变换到数轴为例，观察各基向量的变化。

?1）在二维空间中放上一条一维数轴，其中 $\hat{u}$ 为该数轴的单位向量，0位置是二维空间的原点：

2）二维空间基向量? $\begin{bmatrix} \hat{i}\\ \hat{j} \end{bmatrix}$ ?变换到数轴上的情形：

这不就是投影嘛！

3）确定二维基向量投影到数轴单位向量上的位置坐标：

基向量? $\hat{i}$ 在数轴的单位向量 $\hat{u}$ 上的投影就是单位向量 $\hat{u}$ 在x轴上的投影！（虚线部分表示对称轴，而且 $\hat{i},\hat{j},\hat{u}$ 的长度都是单位1）。同理， $\hat{j}$ 在数轴的单位向量 $\hat{u}$ 上的投影就是单位向量 $\hat{u}$ 在y轴上的投影：

4）此时，我们就得到了二维基向量变换到数轴上的位置，用一个 $1\times 2$ 的矩阵表示为 $\begin{bmatrix} u_{x}& u_{y} \end{bmatrix}$ ，即变换矩阵，也叫投影矩阵。

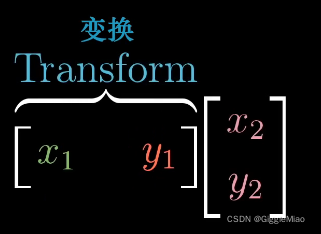
· 有了基向量的变换，回忆之前所讲的，任何向量 $\begin{bmatrix} x\\ y \end{bmatrix}$ 的变换结果只需该向量在变换后的基向量上表达出来就可以了，形式为基变换矩阵和向量的相乘 $\begin{bmatrix} u_{x}& u_{y} \end{bmatrix}$ $\begin{bmatrix} x\\ y \end{bmatrix}$ 。并且，从计算结果来看，与单位向量和 $\begin{bmatrix} x\\ y \end{bmatrix}$ ?的点积是一样的。

?因此，任意向量之间的点积可以解读为是一个向量1朝给定向量2（将该向量所在直线看作是变换后的数轴）做投影（理解为二维空间的基变换）再将投影值与给定向量2长度相乘（也就是基的投影变换矩阵乘以任意向量2，相当于向量2在基变换矩阵下的线性组合形式）。

从表面上看，点积是理解投影的有利几何工具，并且方便检验两个向量的方向是否相同。更进一步来说，两个向量点乘，就是将其中一个向量转化为线性变换（理解为投影实现的）。

?=?

当看到一个线性变换的输出空间是一维数轴上的值，则在原来的多维空间中都会存在唯一的向量与之对应，这就是对偶性。（只可意会吧。。）?