[人工智能] 基于泰坦尼克号数据对现实生存法则的研究分析

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 基于泰坦尼克号数据对现实生存法则的研究分析 -> 正文阅读

[人工智能]基于泰坦尼克号数据对现实生存法则的研究分析

基于泰坦尼克号数据对现实生存法则的研究分析

电影泰坦尼克号中，船体下沉时，船长命令妇女儿童先上救生艇，确实让人感受到人性的伟大，但是事实是否真的如此，现实的生存法则到底是否是真的残酷，还是值得深入考究。本文利用部分泰坦尼克号乘客数据，运用关联分析，得到有关乘客是否成功获救的关联规则；通过决策树模型，对乘客进行画像，深入探究乘客获救与否的特征。

思路

1 引言

1912年4月14日，号称“永不沉没”的邮轮–泰坦尼克号撞上冰山，发生船难。同时这一真实事件也被翻拍成电影，电影中，船体发生断裂不可逆转的下沉开始时，船长命令妇女和儿童先上救生艇，但是现实生存法则还是值得深思，毕竟社会结构的力量一直都在，当时的贵族阶级是否真的会展现自己人性的光辉。有人可能会质疑这是艺术美化后的场景，真实的历史没有那么感人。现实的生存法则就是舱位等级决定了你的生还几率，而不是你是否为妇女或儿童。因此，本文借泰坦尼克号数据集探寻乘客幸存的因子，在灾难面前，是妇孺优先，还是阶级至上。

2 数据简介

本次研究的数据描述泰坦尼克号的乘客数据，数据资料包括乘客ID、是否存活、乘客等级、名字、性别、年龄、与乘客同行的兄弟姐妹和配偶数目、与乘客同行的家长和孩子数目、船票号、乘客费用、船舱、登船港口。共计891条数据。

变量	属性
乘客ID（PassengerId）	连续型数值
是否存活（Survived）	否（No）、是（Yes）
乘客等级（Pclass）	一等舱位（1）、二等舱位（2）、三等舱位（3）
名字（Name）	名（first name）、称谓（title）、姓（last name）
性别（Sex）	男性（Male）、女性（Female）
年龄（Age）	连续型数值
与乘客同行的兄弟姐妹和配偶数目（SibSp）	离散型数值
与乘客同行的家长和孩子数目（Parch）	离散型数值
船票号（Ticket）	船票编号
乘客费用（Fare）	连续型数据
船舱（Cabin）	仓位号和房间编号
登船港口（Embarked）	Cherbourg（C）、Queenstown（Q）、Southampton（S）

3 简单的描述性分析

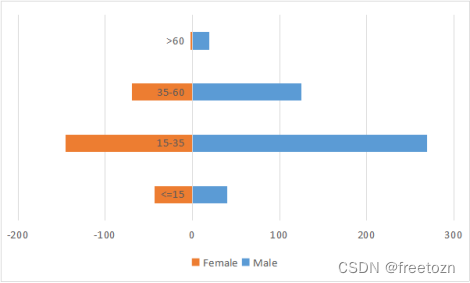
男女性年龄基本情况
整艘邮轮男女比例不均衡，男性占比较大。根据年龄层次看出，邮轮群体主要集中在15-35岁，即青年居多。
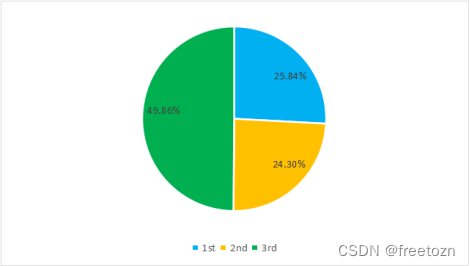
不同等级占比
三等舱位人数接近总体的一半，二等舱位和三等舱位的人数较均衡。

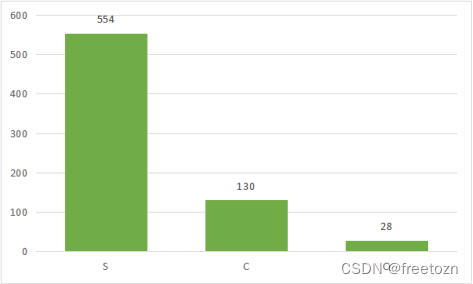
登船港口基本情况
多数乘客登船位置为Southampton，即英国的南安普顿港，正是泰坦尼克号的起点港湾。途经法国瑟堡、新西兰皇后镇。
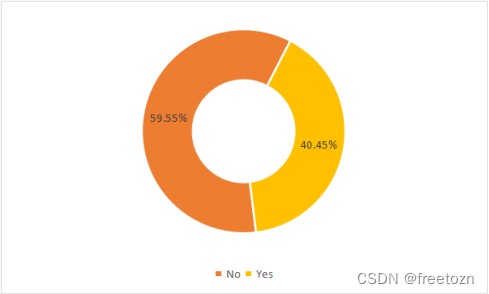
乘客幸存占比
可能数据只选择了训练集，因此获救率与未获救率差距不大。但是整体上看，泰坦尼克号船难获救率不到一半，灾难面前还是很残酷的。

4 数据建模与分析

4.1 乘客信息与存活与否的关联分析

4.1.1 成功获救的乘客特征挖掘

本项目首先使用关联规则挖掘方法（Apriori）挖掘成功获救的乘客特征。在支持度大于9%的前提下，得到置信度最大的五个关联规则，结果如下表所示：
由上表可得，第一个关联规则的支持度为11.2%，说明成功获救的一等舱位的女性占比11.2%；其置信度为96.4%，说明一等舱位的女性成功获救的概率为96.4%；其提升达到了2.383，说明一等舱位的女性成功获救对于整体获救概率提升了1.383倍。
第二个关联规则的支持度为9.6%，说明成功获救的二等舱位的女性占比9.6%；其置信度为91.9%，说明二等舱位的女性成功获救的概率为97.2%；其提升达到了2.272，说明二等舱位的女性成功获救对于整体获救概率提升了1.272倍。
第三个关联规则的支持度为15.7%，说明成功获救的青年女性占比15.7%；其置信度为77.2%，说明青年女性成功获救的概率为77.2%；其提升达到了1.910，说明青年女性成功获救对于整体获救概率提升了0.910倍。
第四个关联规则的支持度为27.4%，说明成功获救的女性占比27.4%；其置信度为75.3%，说明女性成功获救的概率为75.3%；其提升达到了1.861，说明女性成功获救对于整体获救概率提升了0.861倍。
第五个关联规则的支持度为18.7%，说明成功获救的登船港口为S的女性占比18.7%；其置信度为71.5%，说明登船港口为S的女性成功获救的概率为71.5%；其提升达到了1.768，说明登船港口为S的女性成功获救对于整体获救概率提升了0.768倍。
综上所述，位于一、二舱位的女性、青年女性获救率较高。

4.1.2 未成功获救的乘客特征挖掘

同理，本项目继续挖掘未成功获救的乘客特征，在支持度大于30%前提下，得到置信度最大的五个关联规则，结果如下表所示：

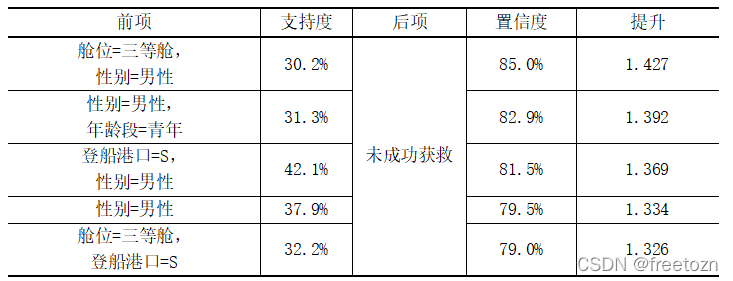
由上表可得，第一个关联规则的支持度为30.2%，说明未被获救的三等舱位的男性占比30.2%；其置信度为85.0%，说明三等舱位的男性未被获救的概率为85.0%；其提升达到了1.427，说明三等舱位的男性未被获救对于整体未获救概率提升了0.427倍。
第二个关联规则的支持度为31.3%，说明未被获救的青年男性占比31.3%；其置信度为82.9%，说明青年男性未被获救的概率为82.9%；其提升达到了1.392，说明青年男性未被获救对于整体未获救概率提升了0.392倍。
第三个关联规则的支持度为42.1%，说明未被获救的登船港口为S的男性占比42.1%；其置信度为81.5%，说明登船港口为S的男性未被获救的概率为81.5%；其提升达到了1.369，说明登船港口为S的男性未被获救对于整体未获救概率提升了0.369倍。
第四个关联规则的支持度为37.9%，说明未被获救的男性占比37.9%；其置信度为79.5%，说明男性未被获救的概率为79.5%；其提升达到了1.334，说明男性未被获救对于整体未获救概率提升了0.334倍。
第五个关联规则的支持度为32.2%，说明未被获救的三等舱位登船港口为S的群体占比32.2%；其置信度为79.0%，说明三等舱位登船港口为S的群体未被获救的概率为79.0%；其提升达到了1.326，说明三等舱位登船港口为S的群体未被获救对于整体未获救概率提升了0.326倍。
综上所述，三等舱位的群体、男性、青年男性的获救率较低。

4.2 基于决策树建立存活与否的乘客画像

4.2.1 决策树的构建

为了明确泰坦尼克号中幸存的乘客特征，对数据进行决策树分析建立乘客幸存画像。以下是对数据的预处理：
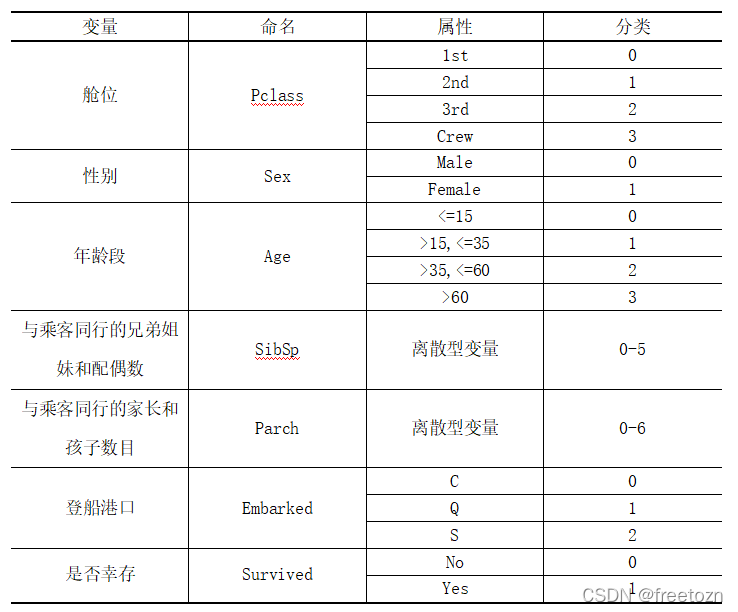
数据预处理表
对预处理后的数据筛选出训练数据和测试数据，本次模型中随机抽取了总数据集的80%作为训练集，20%的数据集作为测试集。训练集和测试集划分完成后，我们将训练集用来构建分类树，从而获取不同价格区间的用户画像。因分枝数较多，进行剪枝操作。利用十折交叉验证和网格搜索法确定建立决策树的最优参数，因此得出的参数为信息熵作为评判标准,，决策树最大深度为6，叶节点所需的最小样本数为1，由此建立决策树模型。

4.2.2 模型结果分析

决策树模型! 由决策树模型得出乘客是否被获救的画像，成功获救的乘客：（1）登船港口为法国一等舱位的男性青少年；（2）二等舱位，少年，至少跟随一位家长；（3）一、二等舱位的女性；（4）登船港口为法国和新西兰的女性。未被成功获救的乘客：（1）登船港口为新西兰和英国的一等舱位的男性；（2）登船港口为法国的一等舱位的中老年男性；（3）二、三等舱位的男性，并且不带家长或孩子；（4）二、三舱位的男性青少中年，至少带一个家长或孩子；（5）三等舱位的男性少年，至少跟随一位家长；（6）三等舱位的中老年女性；（7）登船港口为英国的三等舱位的女性青少年。

5 结论与思考

无论是关联规则的结果，还是决策树模型的画像，都可以看出女性的获救率大于男性，少年的获救率大于中老年的获救率。但是无论是女性还是少年都是以阶级为基础的，结果表明是作为一、二等舱位的女性，亦或是一、二等舱位的少年才有较高的获救率。由上决策树的结果看出三等舱位的女性青少年并不能成功获救。因此，在一定程度上，“现实的生存法则就是舱位等级决定了你的生还几率”这句话不无道理。相同等级下可能是妇女儿童优先率更高，从整体上看，还是阶级至上的。

6 参考文献

晋军.结构的力量:“泰坦尼克号”上的生与死[J].读书,2016(08):77-83.
王蕾.评电影《泰坦尼克号》所折射出的人性光辉[J].电影文学,2013(09):121-122.
袁馨,段华琼.基于决策树算法对泰坦尼克号数据的预测[J].电脑知识与技术,2020,16(22):185-186+199.
吴敏之.泰坦尼克号的真正秘密[J].世界科学,1995(12):22-23+21.
温德涌.“泰坦尼克号”海难事故引发的思考[J].武汉船舶职业技术学院学报,2006(02):20-22.
高洪涛.基于关联规则探究数据挖掘与应用[J].信息与电脑(理论版),2020,32(02):126-127+130.

7 代码展示

7.1 准备工作

#准备工作
import pandas as pd
import numpy as np
from sklearn import metrics
from sklearn.metrics import classification_report
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt

data=pd.read_csv('titanic.csv')#读取数据
data.drop(columns = ['Cabin'],inplace=True)#剔除Cabin（空值实在太多）
data.dropna(axis=0, how='any', thresh=None, subset=None, inplace=True)#剔除存在空值的行
data#展示数据

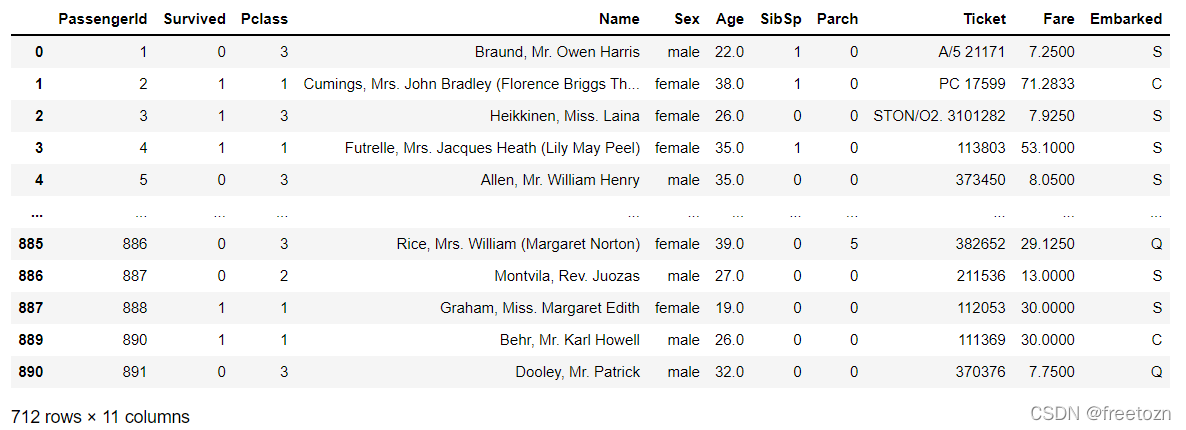
在这里插入图片描述

data.index = range(0, 712)#给清洗过后的数据添加索引
data#再次展示数据

在这里插入图片描述

7.2 决策树代码

#处理性别
data['Sex'][data['Sex']=='male']=0
data['Sex'][data['Sex']=='female']=1

#处理年龄
data['Age']=data['Age'].astype('int')#年龄字段转换为整数型
for i in range(712):
    if data['Age'].loc[0:,][i]<=15:
        data['Age'].loc[0:,][i]=0
    elif data['Age'].loc[0:,][i]>15 and data['Age'].loc[0:,][i]<=35:
        data['Age'].loc[0:,][i]=1
    elif data['Age'].loc[0:,][i]>35 and data['Age'].loc[0:,][i]<=60:
        data['Age'].loc[0:,][i]=2
    else:
        data['Age'].loc[0:,][i]=3

#量化登船港口编号
data['Embarked'][data['Embarked']=='C']=0
data['Embarked'][data['Embarked']=='Q']=1
data['Embarked'][data['Embarked']=='S']=2

X=data.iloc[:,[2,4,5,6,7,10]]#提取特征值
Y=data['Survived']
data.columns[[2,4,5,6,7,10]]#查看列
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(X, Y, test_size=0.2)#划分训练集和测试集
for i in [x_train, x_test, y_train, y_test]:#修正训练集和测试集的索引
    i.index = range(i.shape[0])
#查看分好的训练集和测试集
x_train

在这里插入图片描述

clf = tree.DecisionTreeClassifier()#生成实例
clf = clf.fit(x_train, y_train)
tree_y_pred = clf.predict(x_test)#生成预测值
tree_y_pred

在这里插入图片描述

metrics.accuracy_score(y_test,tree_y_pred)#真实值与预测值的一致性
cnf_matrix = metrics.confusion_matrix(y_test,tree_y_pred)#输出混淆矩阵
print(classification_report(y_test,tree_y_pred))#打印出决策树的模型评价

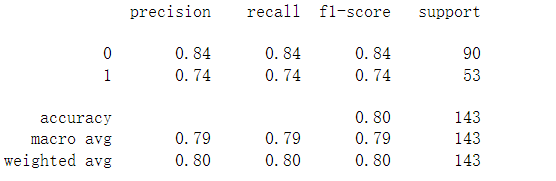
在这里插入图片描述

import graphviz#导入graphviz模块

注意：该模块需要外部导入安装
在这里插入图片描述
需要下载该安装包，勾选路径（第二个第三个都可以），然后重启jupyter或运行代码的某一个工具

tree.plot_tree(clf)#生成决策树规则
#训练集与测试集进行拟合
tr = []
te = []
for i in range(10):
    clf = DecisionTreeClassifier(random_state=25,max_depth=i+1,criterion="entropy")
    clf = clf.fit(x_train, y_train)
    score_tr = clf.score(x_train,y_train)
    score_te = cross_val_score(clf,X,Y,cv=10).mean()
    tr.append(score_tr)
    te.append(score_te)
print(max(te))
plt.plot(range(1,11),tr,color="red",label="train")
plt.plot(range(1,11),te,color="blue",label="test")
plt.xticks(range(1,11))
plt.legend()
plt.show()

#利用网络搜索法需求最优解（这里需要耐心等待，会很慢才出结果）
import numpy as np
gini_thresholds = np.linspace(0,0.5,20)
parameters = {'splitter':('best','random'),'criterion':("gini","entropy"),"max_depth":[*range(1,10)],'min_samples_leaf':[*range(1,50,5)],'min_impurity_decrease':[*np.linspace(0,0.5,20)]}
clf = tree.DecisionTreeClassifier(random_state=25)
GS = GridSearchCV(clf, parameters, cv=10)#交叉验证
GS.fit(x_train,y_train)
GS.best_params_#最优解
GS.best_score_#最优评价

在这里插入图片描述

clf = tree.DecisionTreeClassifier(criterion='gini',max_depth=6,min_impurity_decrease=0.0,min_samples_leaf=6,splitter= 'random')
#利用最优解建立决策树
clf = clf.fit(x_train, y_train)#训练数据集
tree_y_pred = clf.predict(x_test)#生成预测值
tree_y_pred
metrics.accuracy_score(y_test,tree_y_pred)#真实值与预测值的一致性
cnf_matrix = metrics.confusion_matrix(y_test,tree_y_pred)
print(cnf_matrix)
#主对角线上是分类正确的个数，副对角线是分类错误的个数
print(classification_report(y_test,tree_y_pred))#打印出决策树的模型评价
feature_name=data.columns[[2,4,5,6,7,10]]
dot_data = tree.export_graphviz(clf,filled=True,rounded=True,feature_names=feature_name,class_names=['No','Yes'])
graph = graphviz.Source(dot_data)
graph#直接输出决策树

dot_data=dot_data.replace('helvetica','"Microsoft Yahei"') # 修改字体，支持中文
graph = graphviz.Source(dot_data)
graph.render(r'titanic_2')#将可视化结果输出pdf文件至指定位置

7.3 关联规则代码

data=pd.read_csv('titanic.csv')#读取数据
data.drop(columns = ['Cabin'],inplace=True)
data.dropna(axis=0, how='any', thresh=None, subset=None, inplace=True)

#将是否幸存表示为no yes
data['Survived'][data['Survived']==0]='No'
data['Survived'][data['Survived']==1]='Yes'

#将等级英文化
data['Pclass'][data['Pclass']==1]='1st'
data['Pclass'][data['Pclass']==2]='2nd'
data['Pclass'][data['Pclass']==3]='3rd'

#将年龄分级英文化
for i in range(712):
    if data['Age'][i]<=15:
        data['Age'][i]='juvenile'
    elif data['Age'][i]>15 and data['Age'][i]<=35:
        data['Age'][i]='teenager'
    elif data['Age'][i]>35 and data['Age'][i]<=60:
        data['Age'][i]='middle-aged'
    else:
        data['Age'][i]='elderly'

from efficient_apriori import apriori
d=data.iloc[:,[1,2,4,5,10]]#将需要进行关联规则的列取出
d =d.apply(lambda x: tuple(x), axis=1).values.tolist()#将列表变成元组
itemsets,rules=apriori(d,min_support=0.08,min_confidence=0.5)#支持度为0.08，置信度为0.5
itemsets#输出频繁项集
rules#输出规则

rules_rhs=filter(lambda rule:len(rule.lhs)==1 and len(rule.rhs)==1,rules)#前件数为1，后件数为1
result=sorted(rules_rhs,key=lambda rule:rule.lift)#对规则进行排序
for rule in result:
    print(rule)#输出排序后的关联规则

rules_rhs=filter(lambda rule:len(rule.lhs)==2 and len(rule.rhs)==1,rules)#前件数为2，后件数为1
result=sorted(rules_rhs,key=lambda rule:rule.lift)#对规则进行排序
for rule in result:
    print(rule)#输出排序后的关联规则

rules_rhs=filter(lambda rule:len(rule.lhs)==3 and len(rule.rhs)==1,rules)#前件数为3，后件数为1
result=sorted(rules_rhs,key=lambda rule:rule.lift)#对规则进行排序
for rule in result:
    print(rule)#输出排序后的关联规则

rules_rhs=filter(lambda rule:'Yes' in rule.rhs ,rules)#后件包含"Yes"的关联规则
list(rules_rhs)
rules_rhs=filter(lambda rule:'No' in rule.rhs ,rules)#后件包含"No"的关联规则
list(rules_rhs)