一：什么是空洞卷积：
（因为该内容较长，作者会在文章底部提供本人学习空洞卷积的博客连接，供大家学习参考）
二：空洞卷积的优点：
（1）：增大感受野：
对于普通卷积来说，空洞卷积有效地扩大了每一次运算的视野（在下文有清晰的表示）。
（2）：保持原输入特征图W（宽），H（高）：
也就是说原输入的特征图和特征矩阵不会因为引入空洞卷积而导致输入发生改变。
三：什么是‘gridding effect’问题：
如图所示：
不难看出在此例子当中有四层卷积计算层，而每次的空洞卷积‘dialted rate’（膨胀率）设为2时，在layer4层中利用到layer1层的区域（就是图中不为0的区域，而数字的大小是利用的次数）中间会产生许多缝隙，这会导致利用到的原始数据不连续（中间有许多数字为0的区域），会导致有很多细节会缺失，这种问题就是‘gridding effect’问题。-
四：设计不会产生‘gridding effect’现象的‘dialted rate’选用原则
（1）：
原则：
如下图公式：
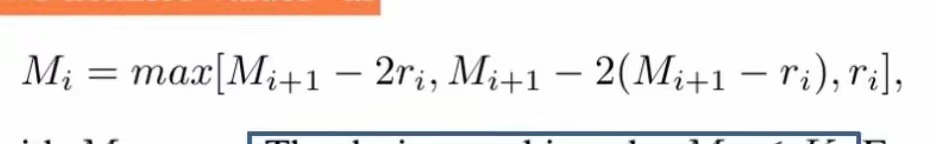
图中:
：第i层的膨胀系数
就举个例子来说r=[1,2,5]??? =max[5-2*2,5-2*(5-2),2]=2?? （K是kernel size 卷积核的第一个维度数，这里设置的是3）
有K=3>==2,所以成立，不会出现‘gridding effect’问题，如下图，全部区域都有用到：
（2）：将‘dialted rate’设计成锯齿结构：
简单来讲就是重复所给定的一组系数，如r=[1,2,3,1,2,3],r=[1,2,5,1,2,5]类似这种格式，也不会出现‘gridding effect’问题。
（3）：设置的‘dialted rate’公约数不能大于一：
如r=[2,4,6]这组公约数为2大于1所以会出现‘gridding effect’问题，如图：（很明显有很多区域没有被利用）
https://blog.csdn.net/weixin_40519315/article/details/105115649