Neural Networks
Model Representation I
How we represent our hypothesis or how we represent our model when using neural networks?
- neurons are cells in the brain
- neuron has a cell body
- neuron has a number of input wires( dendrites, receive inputs from other locations)
- has an output wire ( Axon)
Communicate with little pulses of electricity (also called spikes)
Doing computations and passing messages to other neurons as a result of what other inputs they’ve got.
-Do Computation
- output some value on this output wire, or
in the biological neuron, this is an axon
- where it gets a number of inputs, x1,
x2, x3 and it outputs some value computed.
- x0, the bias unit or the bias neuron
Sigmoid(logestic) activiation function( g ( z ) = 1 1 + e ? z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e?z1?)
A simplistic representation looks like:
[ x 0 x 1 x 2 ] → [ ?? ] → h θ ( x ) [x_0x_1x_2]\rightarrow[\;]\rightarrow h_\theta(x) [x0?x1?x2?]→[]→hθ?(x)
( h θ ( x ) = 1 1 + e ? θ T X h_\theta(x)=\frac{1}{1+e^{-\theta^TX}} hθ?(x)=1+e?θTX1?)
“input layer”(layer 1) → \rightarrow →layer 2 → \rightarrow →"output layer"(layer 3)
have intermediate layers of nodes between the input and output layers called the "hidden layers"
“weights”(权重)=“parameter”
notation:
? a i ( j ) a_i^{(j)} ai(j)?:第j层的第i个神经元或单元的激活项
? Θ ( j ) \Theta^{(j)} Θ(j):权重矩阵,控制从第j层到第j+1层的映射
If we have one hidden layer, it would look like:
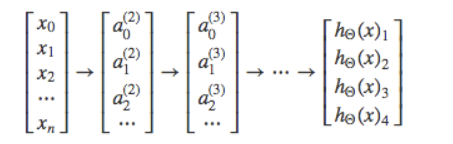
[ x 0 x 1 x 2 x 3 ] → [ a 1 ( 2 ) a 2 ( 2 ) a 3 ( 2 ) ] → h θ ( x ) [x_0x_1x_2x_3]\rightarrow[a_1^{(2)}a_2^{(2)}a_3^{(2)}]\rightarrow h_\theta(x) [x0?x1?x2?x3?]→[a1(2)?a2(2)?a3(2)?]→hθ?(x)
The values for each of the “activation” nodes is obtained as follows:
? a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a_1^{(2)}=g(\Theta_{10}^{(1)}x_0+\Theta_{11}^{(1)}x_1+\Theta_{12}{(1)}x_2+\Theta_{13}^{(1)}x_3) a1(2)?=g(Θ10(1)?x0?+Θ11(1)?x1?+Θ12?(1)x2?+Θ13(1)?x3?)
? a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a_2^{(2)}=g(\Theta_{20}^{(1)}x_0+\Theta_{21}^{(1)}x_1+\Theta_{22}{(1)}x_2+\Theta_{23}^{(1)}x_3) a2(2)?=g(Θ20(1)?x0?+Θ21(1)?x1?+Θ22?(1)x2?+Θ23(1)?x3?)
? a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) a_3^{(2)}=g(\Theta_{30}^{(1)}x_0+\Theta_{31}^{(1)}x_1+\Theta_{32}{(1)}x_2+\Theta_{33}^{(1)}x_3) a3(2)?=g(Θ30(1)?x0?+Θ31(1)?x1?+Θ32?(1)x2?+Θ33(1)?x3?)
h Θ ( x ) = a 1 ( 3 ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) h_\Theta(x)=a_1^{(3)}=g(\Theta_{10}^{(2)}a_0^{(2)}+\Theta_{11}^{(2)}a_1^{(2)}+\Theta_{12}^{(2)}a_2^{(2)}+\Theta_{13}^{(2)}a_3^{(2)}) hΘ?(x)=a1(3)?=g(Θ10(2)?a0(2)?+Θ11(2)?a1(2)?+Θ12(2)?a2(2)?+Θ13(2)?a3(2)?)
如果一个网络在第j层有 s j s_j sj?个单元,在j+1层有 s j + 1 s_{j+1} sj+1?个单元,那么矩阵 Θ j \Theta_j Θj?即控制第j层到第j+1层映射的矩阵,它的维度是** s j + 1 × s j + 1 s_{j+1}\times s_{j}+1 sj+1?×sj?+1**
Model Representation II
Vectorize
a 1 ( 2 ) = g ( z 1 ( 2 ) ) a_1^{(2)}=g(z_1^{(2)}) a1(2)?=g(z1(2)?)
a 2 ( 2 ) = g ( z 2 ( 2 ) ) a_2^{(2)}=g(z_2^{(2)}) a2(2)?=g(z2(2)?)
a 3 ( 2 ) = g ( z 3 ( 2 ) ) a_3^{(2)}=g(z_3^{(2)}) a3(2)?=g(z3(2)?)
for layer j=2 and node k, the variable z will be:
z k ( 2 ) = Θ k , 0 ( 1 ) x 0 + Θ k , 1 ( 1 ) x 1 + . . . + Θ k , n ( 1 ) x n z_k^{(2)}=\Theta_{k,0}^{(1)}x_0+\Theta_{k,1}^{(1)}x_1+...+\Theta_{k,n}^{(1)}x_n zk(2)?=Θk,0(1)?x0?+Θk,1(1)?x1?+...+Θk,n(1)?xn?
vector repretation of x and
z
j
z^j
zj:
x
=
[
x
0
x
1
.
.
.
x
n
]
z
(
j
)
=
[
z
1
(
j
)
z
2
(
j
)
.
.
.
z
n
(
j
)
]
x=\begin{bmatrix}x_0\\x_1\\...\\x_n\end{bmatrix}\quad z^{(j)}=\begin{bmatrix} z^{(j)}_1\\z^{(j)}_2\\...\\z^{(j)}_n\end{bmatrix}
x=?????x0?x1?...xn???????z(j)=??????z1(j)?z2(j)?...zn(j)????????
setting
x
=
a
(
1
)
x=a^{(1)}
x=a(1), we can write the equation as:
z ( j ) = Θ ( j ? 1 ) a ( j ? 1 ) z^{(j)}=\Theta^{(j-1)}a^{(j-1)} z(j)=Θ(j?1)a(j?1)
Θ ( j ? 1 ) \Theta^{(j-1)} Θ(j?1) is matrix with dimensions s j × ( n + 1 ) s_j\times (n+1) sj?×(n+1) (where s j s_j sj? is the number of our activation nodes) by our vector a ( j ? 1 ) a^{(j-1)} a(j?1) with height (n+1). This gives us our vector z ( j ) z^{(j)} z(j) with height s j s_j sj?
for layer j:
a ( j ) = g ( z ( j ) ) a^{(j)}=g(z^{(j)}) a(j)=g(z(j)), g can be applied element-wise to vector z ( j ) z^{(j)} z(j)
After we have computed a ( j ) a^{(j)} a(j), we can add a bias unit(equals to 1) to layer j.
add a 0 ( j ) a^{(j)}_0 a0(j)?=1
first compute another z z z vector: z ( j + 1 ) = Θ ( j ) a ( j ) z^{(j+1)}=\Theta^{(j)}a^{(j)} z(j+1)=Θ(j)a(j)
get the final z z z vector by multiplying the next theta matrix after Θ ( j ? 1 ) \Theta^{(j-1)} Θ(j?1) with the values of all the activation nodes we just got. This last theta matrix Θ ( j ) \Theta^{(j)} Θ(j)will have only one row which is multiplied by one column$ a^{(j)}$ so that our result is a single number. We then get our final result with:
h Θ ( x ) = a ( j + 1 ) = g ( z ( j + 1 ) ) h_\Theta(x)=a^{(j+1)}=g(z^{(j+1)}) hΘ?(x)=a(j+1)=g(z(j+1))
Notice that in this last step, between layer j and layer j+1, we are doing exactly the same thing as we did in logistic regression.
前向传播(forward propagation)
Applications
Non-linear classification example: XOR/XNOR
$x_1,x_2 $are boundary(0 or 1)
y = x 1 X O R x 2 y=x_1XOR x_2 y=x1?XORx2? 当 x 1 和 x 2 x_1和x_2 x1?和x2?中恰好有一个的值等于1则为真(y=1)
? x 1 X N O R x 2 x_1 XNOR x_2 x1?XNORx2? 当正样本同时为真或同时为假时y=1
? ( N O T ( x 1 X O R x 2 ) NOT(x_1XOR x_2) NOT(x1?XORx2?))
Simple example: AND
x 1 , x 2 ∈ 0 , 1 x_1,x_2\in{0,1} x1?,x2?∈0,1
y = x 1 A N D x 2 y=x_1 AND x_2 y=x1?ANDx2?
加偏置单元(+1单元)以计算只有单个神经元的神经网络来计算这个AND函数
对权重(参数)赋值
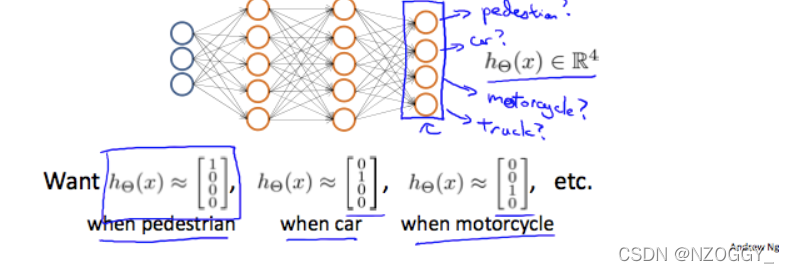
Multi-class classification