李宏毅机器学习课程笔记
--深度学习基本概念简述
前言
从零入门机器学习。李宏毅2021春机器学习课程笔记
第2篇 深度学习基本概念简述
上一篇用y=b+w*x来拟合数据,得到的结果并非让人满意,在这里我们将之前的三步都升级一下,使之更加实用。我们所研究的很少有数据符合这样简单的线性关系,现实中的可能是一段段折线,或是一条蜿蜒的曲线。那我们就要用一个更好的方程来表达这样的线。
1.如何更好地拟合实际情况:
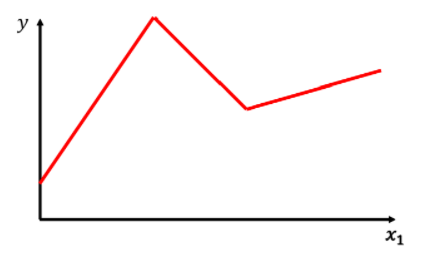
为了拟合这样的线段(红色),我们要用到一个蓝色的函数:

这个函数可以认为是在x<a,x>b时,为定值.在x属于(a,b)时为一段比例函数
对于上面的红色线段,我们可以用这样的方式来拟合

由此我们可以用一个常数,加上三个蓝色函数的组合来得到红色线段
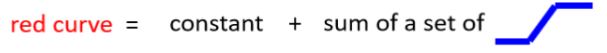
由此类推,对于所有的折线,我们都可用类似的组合来表示,区别只是不同蓝色函数的数量多少。
那么对于曲线也可通过采点再描线的方式来拟合,只要点够多,就可以足够接近。
但是这样的蓝色函数不太好表达出来,我们可以用一个更好表达且效果相同的函数:
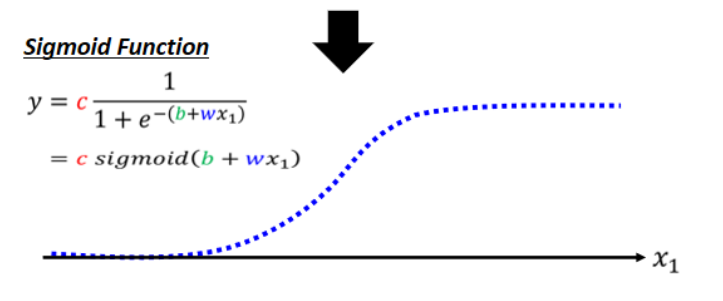
这个函数比较好理解,在x趋向无穷大时,分母趋向于1,y趋向于c; 在x趋向于无穷小时,y趋向于0.
为了获得不同的sigmoid函数,我们可以改变c,b,w的值,他们对应的作用如下图:

有了以上工具,我们就可以用这个式子来表示复杂方程了:
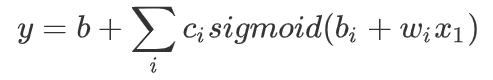
同样地,对于Youtube频道点阅人数的预测,如果我们考虑变化的周期,即多天的情况综合输入。
以前我们是:
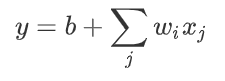
现在我们就可以这样:
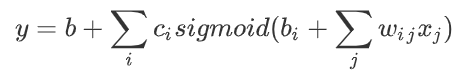
更加直观的看:
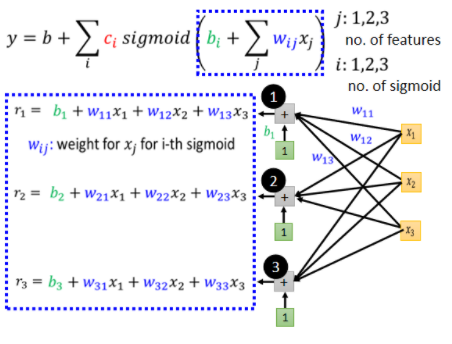
蓝色方框里的很像非齐次方程组,我们可以用线代中矩阵来简化地表达:
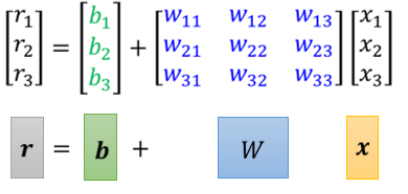
这里所得到的r向量就是上面式子中sigmoid函数的参数,我们用一个符号来表示sigmoid函数,便得到
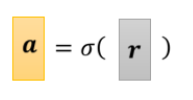
所以之前的式子:
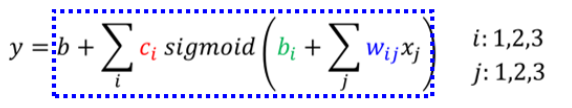
就可以简写为:(只是换了种写法而已)
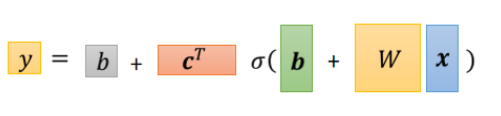
这里的C是一组列向量,为了能够矩阵相乘,要先进行转置操作。
在这个式子里,我们想得到的未知参数为:
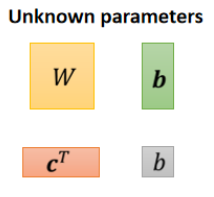
我们将其中的参数全部拉长排列成一列,形成一个长长的列向量,称之为θ
2.定义损失函数loss
在之前,我们把w,b带入然后得到一组预测值,并和实际值比较,然后得到差值,就是我们定义的loss.现在依然如此,只是未知参数变得多了,我们所有的未知参数都定义为θ这个很长的列向量。将θ带入,像之前一样得到loss.
3 寻找最优
我们现在的 θ 它是一个很长的向量,我们把它表示成 θ1 θ2 θ3 等等等,我们现在就是要找一组 θ,这个 θ 可以让我们的 Loss 越小越好,依然是定起始点,求微分,更新参数:

4.模型套娃
我们可以将以上的模型多套几层:
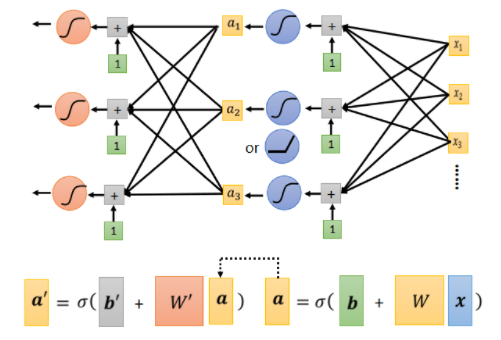
也就是上一层的输出作为下一层的输入继续处理。通常这样反复套娃都会提高识别的正确率,直到过拟合。这也就是被称为deep learning.
那么这里就会有个疑惑,既然都是为了更好地拟合曲线,我不仅可以用这样套娃式,我还可以用很多很多个sigmoid来拟合曲线,并非是纵向套娃,而是继续叠加激活函数一样可以做到十分地接近,但这种为什么不行呢?
老师原话:把 ReLU Sigmoid Function 反覆用,到底有什麼好处呢,為什麼不把它们直接排一排呢,直接排一排也可以表示任何 Function 啊,所以把它反覆用没什麼道理啊,所以有人就说把 Deep Learning,把 ReLU Sigmoid 反覆用,不过是个噱头,你之所以喜欢 Deep Learning,只是因為 Deep 这个它名字好听啦,ReLU Sigmoid 排成一排,你只可以製造一个肥胖的 Network,Fat Neural Network,跟 Deep Neural Network 听起来,量级就不太一样,Deep 听起来就比较厉害啦,Fat Neural Network 还以為是死肥宅 Network,就不厉害这样子,那到底 Deep 的理由,為什麼我们不把 Network 变胖,只把 Network 变深呢,这个是我们日后要再讲的话题