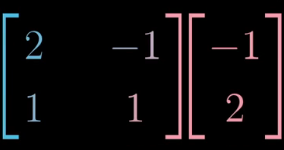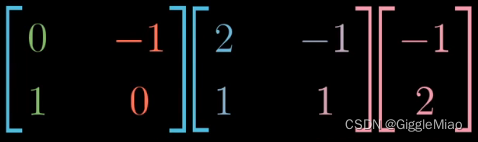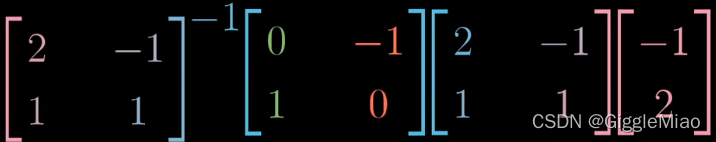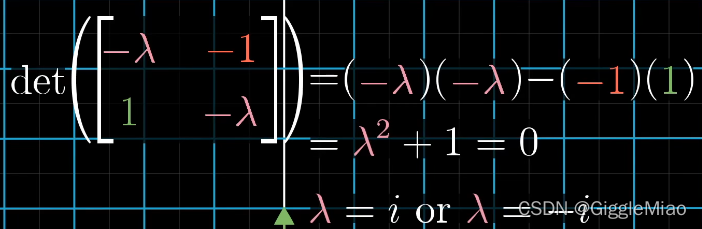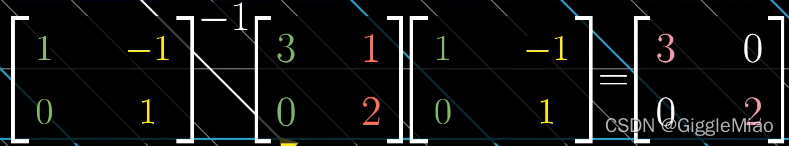[人工智能] 线性代数的本质3

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 线性代数的本质3 -> 正文阅读

[人工智能]线性代数的本质3

干货满满~ 二刷《线性代数的本质》，内容不难，很有助于打开思维。系列文章会尽量把精华都摘下来，有理解不当处欢迎指出。有兴趣的同学也可以直接去刷视频
【官方双语/合集】线性代数的本质 - 系列合集 (bilibili.com)

基变换

先定义一下不同坐标系下的基向量：

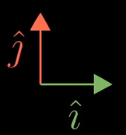
1）在标准坐标系下，即x轴垂直于y轴的坐标系，此时标准基向量表示为 $\begin{bmatrix} \hat{i}\\ \hat{j} \end{bmatrix}$ ?：

2）在非标准坐标系下，基向量会有所不同，比如存在一组基向量? $\begin{bmatrix} \vec{b_{1}}\\ \vec{b_{2}} \end{bmatrix}$ ?：

?

之前的学习我们知道，向量的表示依赖于基的选择，即某个坐标（标量）作用在基上的表达。其中坐标值是对基的缩放程度。那么，当使用不同的基时，向量? $\vec{v}$ ?如何表达？

通过之前的学习我们知道，说到向量的变化，就要考虑到空间中的变换，而说到变换呢，就要去观察基的变换情况，找到了基的变换，向量也就随之确定了。

所以，当基向量由 $\begin{bmatrix} \hat{i}\\ \hat{j} \end{bmatrix}$ 变为 $\begin{bmatrix} \vec{b_{1}}\\ \vec{b_{2}} \end{bmatrix}=\begin{bmatrix} 2 &-1 \\ 1& 1 \end{bmatrix}$ 时，也就相当于基变换矩阵为 $\begin{bmatrix} 2 &-1 \\ 1& 1 \end{bmatrix}$ ，记作A。这个基变换矩阵相当于在标准坐标轴下进行的变换（可以理解为把非标准坐标轴上的基翻译成了在标准坐标轴上的表示），并不是转换到了非标准坐标轴上。?

此时，任何在非标准坐标轴中的向量 $\vec{v}$ 表示在标准坐标轴中的形式为? $\vec{w}=A\vec{v}$ 。

反过来，任何在标准坐标轴中的向量 $\vec{w}$ 在非标准坐标轴上的表示形式为? $\vec{v}=A^{-1}\vec{w}$ 。

举例

比如将非标准坐标系中基为 $\begin{bmatrix} 2 &-1 \\ 1& 1 \end{bmatrix}$ ，其中向量 $\begin{bmatrix} -1\\ 2 \end{bmatrix}$ 逆时针旋转90°，在非标准坐标系中应该怎么表达？

1）由于基的不同，所以非标准坐标系中向量逆时针旋转90°的矩阵并不是 $W=\begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix}$ 。因此需要先在标准坐标系下变换之后再转换到非标准坐标系中表示。

向量?? $\vec{v}=\begin{bmatrix} -1\\ 2 \end{bmatrix}$ 在标准坐标轴上表达为 $A\vec{v}$ ：

2）标准坐标系下，基向量逆时针旋转90°，基变换矩阵为W，则向量在标准坐标系下逆时针旋转90°的结果为左乘基变换矩阵 $WA\vec{v}$ ：

3）最后将标准坐标系中变换好的向量“翻译”回非标准坐标系，左乘逆矩阵，为 $A^{-1}WA\vec{v}$ ?：

总结：其实向量是在做着同样的事，只不过在表达上需要借助标准坐标轴的“转译”。先应用基变换，然后应用线性变换，最后应用基变换的逆，从而得到非标准坐标轴上变换的表达。

推广：当我们看到 $A^{-1}WA\vec{v}$ 的形式时，W代表着空间上的某种线性变换，而 $A$ 和 $A^{-1}$ 则代表这不同视角（坐标系）的转化。

?特征值与特征向量

这一节的内容是真的绝！

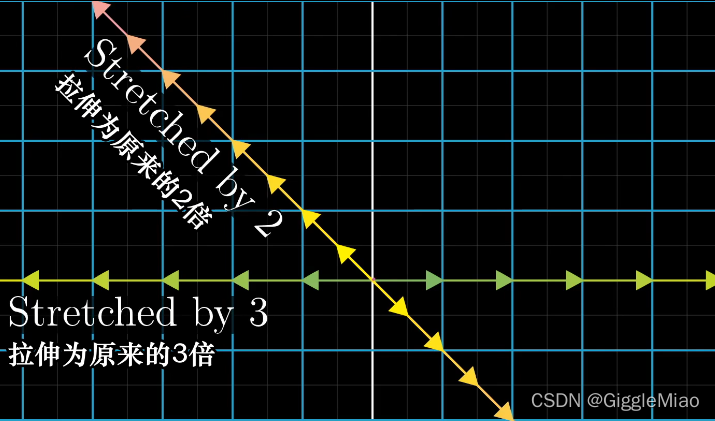
空间在经过某种变换之后，有些向量仍然会留在自身的空间里。以二维向量为例，就是说一个向量在经过变换之后依然保持在同一条直线上（保留在该向量所在的一维数轴中）?。意味着变换矩阵对这些向量的作用只是拉伸或压缩而已，相当于这些向量乘以一个标量。这时，我们就说，这些变换后仍留在原本空间中的向量为特征向量，而变换对这些特征向量对应缩放的系数，就是特征值。

举例说明

在二维空间中，存在一个 $\begin{bmatrix} 3 & 1\\ 0& 2 \end{bmatrix}$ 的线性变换，该空间中的大部分向量经过变换后都会有或多或少的旋转，而—— 1) 基向量中的 $\hat{i}$ 变成了原来的3倍，仍停留在x轴上，并且由于线性变换的性质，x轴上的其他向量也都被拉伸了3倍，留在了x轴。2) 向量? $\begin{bmatrix} -1& 1 \end{bmatrix}^{T}$ 在经过变换后也留在了自己的数轴上，被拉伸为原来的2倍，同理，因为线性性质，它所在的数轴上任一向量也都被拉伸了2被，留在该数轴上。

所以，对于二维空间中的 $\begin{bmatrix} 3 & 1\\ 0& 2 \end{bmatrix}$ 变换， $\hat{i}$ 所在数轴与向量 $\begin{bmatrix} -1& 1 \end{bmatrix}^{T}$ 所在数轴的向量为特征向量，拉伸的倍数3和2为对应的特征值。

注：特征值也可以为负值，这时说明该向量被反向的缩放，但仍然在原始空间。

特征值和特征向量的求解

前面说矩阵变换对特征向量的作用相当于特征向量乘以一个标量。用符号表示为 $A\vec{v}=\lambda \vec{v}$ ?：

?

这个公式说明，矩阵与特征向量的乘积等于特征值乘以特征向量，?为了求解需要，我们将特征值标量乘以单位矩阵I来进行计算：?

$A\vec{v}=(\lambda I)\vec{v}$ ?

现在两侧都变成了矩阵乘以向量的形式，因此可以移项并提出公共因子：

$A\vec{v}-(\lambda I)\vec{v}=0$

? $(A-\lambda I)\vec{v}=0$ ?

此时，寻找一个向量 $\vec{v}$ ，使得新矩阵 $A-\lambda I$ 与 $\vec{v}$ 的结果为零向量。分两种情况：

1）当向量 $\vec{v}$ 本身就是零向量时，这个等式恒成立。

2）当向量 $\vec{v}$ 不为零向量，乘以一个矩阵变成零向量时，说明这个矩阵变换对空间降维了，而空间被压缩对应的变换矩阵的行列式为0：

$\left | A-\lambda I \right |=0$

此等式可以解出特征值，然后根据不同的特征值代入得出对应的特征向量。

举例

以开始的变换为例，变换矩阵A= $\begin{bmatrix} 3 & 1\\ 0& 2 \end{bmatrix}$ ?，求解特征值:

$\begin{vmatrix} 3-\lambda & 1\\ 0 & 2-\lambda \end{vmatrix}=(3-\lambda)(2-\lambda)=0$

得? $\lambda =3\: ;\!\: \lambda =2$

求解特征向量：

1） $\lambda =2$ 时， $\begin{bmatrix} 1 &1 \\ 0 &0 \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}=\begin{bmatrix} 0\\ 0 \end{bmatrix}$ ，得? $x+y=0$ ，即 $y=-x$ ?这个数轴上的所有向量都为特

征向量，如 $\begin{bmatrix} 1\\ -1 \end{bmatrix}$ 。

2） $\lambda =3$ 时， $\begin{bmatrix} 0 & 1\\ 0& -1 \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}=\begin{bmatrix} 0\\ 0 \end{bmatrix}$ ，得? $y=0,x\in R$ ，即x轴上的所有向量都为特征向量，

如 $\begin{bmatrix} 1\\ 0 \end{bmatrix}$ 。

注1：并不是所有的矩阵变换都存在特征向量，比如逆时针90°的旋转变化，此时空间中的每一个向量在变换后都发生了旋转离开了其张开的空间。而且计算特征值时发现：

特征值为复数，表明其没有特征向量。推广——当特征值为复数时，说明变换一般是某种旋转。

注2：可能出现只有一个特征值，但是特征向量不止在一条直线上的情况。比如变换? $\begin{bmatrix} 2 & 0\\ 0 & 2 \end{bmatrix}$ ，只有唯一的特征值 $\lambda =2$ 。但是平面上的每一个向量都是这个特征值上的特征向量。（思考，此时? $r(A-\lambda I)=0$ ，从二维变到了零向量，说明存在两个维度的自由向量没被留住，所以整个二维空间的向量都是特征向量。）

?特征基

当空间变换后的特征向量多到能选出一个张成全空间的集合，比如二维空间变换矩阵的特征向量所在直线是不同的两条，可以张成一个二维空间。这时，就能变换你的坐标系，将特征向量组成的矩阵A看作是标准坐标系下的基变换矩阵 $A\begin{bmatrix} \hat{i}\\ \hat{j} \end{bmatrix}$ ，然后进行线性变换? $MA\begin{bmatrix} \hat{i}\\ \hat{j} \end{bmatrix}$ ，再进行不同坐标系下的基变换? $A^{-1}MA\begin{bmatrix} \hat{i}\\ \hat{j} \end{bmatrix}$ ，就得到了M变换非标准坐标系下的表示。

示例

还是以本节开头的变换为例：
?

新矩阵必然为对角的，所以可以得到，以特征向量作为基向量，其构成的矩阵为基变换矩阵。然后进行线性变换，再乘以基变换矩阵的逆得到在“新视角”中的表达——一个对角矩阵，且对角线的数值就是基变换矩阵中每一列特征向量所对应的特征值。原因是变换矩阵对特征向量只进行了缩放。

在“新视角”中，得到的矩阵? $\begin{bmatrix} 3 & 0\\ 0 &2 \end{bmatrix}$ ?的每一列既是空间中的基向量，也是矩阵自身作为变换时的特征向量，这种特征向量作为基向量的形式称为特征基。

推广——特征基矩阵是对角矩阵的形式。所以将某矩阵A进行对角化操作时，利用A的特征值作为对角线元素的矩阵即可。并且当见到对角矩阵时，每一列基向量都是特征向量，对角线上的值对应于特征向量的特征值。

注：并不是所有的矩阵都能够对角化。比如剪切变换矩阵? $\begin{bmatrix} 1 &1 \\ 0& 1 \end{bmatrix}$ ，特征值为1，特征向量仅有x=0这一条直线，此时特征向量不能张成全空间（二维），所以坐标系的转化什么的也不成立，也就不能对角化了。

?抽象向量空间

这节主要是把“向量”这个概念抽象化，不把它局限在坐标系中的箭头。进而把线性代数中围绕向量进行的各种变换和运算普适化。

线性变换

之前笼统的说过这个概念，现在给出严格的定义：

当变换或者函数满足“可加性”和“成比例”这两条性质时，就说该变换属于线性的：

例如求导也是一种线性运算，因为它满足这两个性质：

?

?

?把线性代数中的概念给它普适开：