[人工智能]【自然语言处理】【表格问答】简单有效的表格问答模型RCI

一、简介

? 近期，研究人员尝试将预训练技术应用在表格问答领域中并取得了不错的效果，例如表格预训练模型$\text{TAPAS}$和$\text{TABERT}$。

? 本文提出了两种新颖的方法，证明即使不使用预训练技术也能在表格问答上取得优越的表现。这两种方法分别为：

• $\text{RCI?interaction}$，该方法利用基于transformer结构的模型来分别对行和列进行分类，并确定与问题最相关的单元格。
• $\text{RCI?represetation}$，该方法通过将已有表格的嵌入向量进行持久化，从而能够为在线QA系统提供高效的服务。

? 实验表明，$\text{RCI?interaction}$的表现超越了基于大量表格语料进行预训练的模型$\text{TAPAS}$和$\text{TABERT}$，在标准的$\text{WikiSQL}$基准上实现了约3.4%和18.86%的改进。

二、整体思路

? $\text{RCI}$模型的灵感来源于表格问答的两个基本操作：行选择和列选择。将行和列的预测概率进行合并，就能得到表格中所有单元格的概率。将具有最高概率的单元格作为答案返回，或者对表格中的单元格进行高亮来帮助用户定位相关信息。一般来说，要定位答案所在的列比较容易，行会比较难。

三、模型$\text{RCI}$

1. $\text{Interaction}$和$\text{Representation}$

? $\text{RCI}$使用文本匹配来定位答案所在的行或者列，其中一个文本是问题，另一个文本是行或者列。$\text{RCI}$模型有两个版本，分别是$\text{Interaction}$和$\text{Representation}$。$\text{Interaction}$版本会将两个句子进行拼接，然后使用transformer进行分类，是一个标准的文本匹配模型。$\text{Representation}$版本会分别对两个句子进行向量映射，然后比较这两个向量。因此，$\text{Representation}$版本的目标是改善实际应用系统的效率。

? 以列分类器举例，$\text{Interaction}$版本模型将问题和列文本进行拼接后送人transformer中。$\text{Representation}$版本模型则会先对所有的表格进行预处理，为每行或者每列生成一个向量表示。在问答时，问题会被投影成向量，然后与列向量合并后，送入单层网络进行分类。

2. 问题形式化

给定一个$m$行$n$列的表格，其中表头为$H=[h_1,h_2,\dots ,h_n]$，单元格的取值为$V=[v_{i,j}],1\le i\le m,1\le j\le n$。表格问答通常由1个表格、1个问题和一组包含正确答案的单元格位置索引组成。因此，单元格位置的索引记为$T?I\times J,I=1,2,...,m,J=1,2,...,n$。(这种精确的答案位置通常很难获得，因此本文中的模型采用弱监督的方式进行训练，即只要答案字符串在单元格中就为正确答案。)

? 模型的目标是训练出行和列分类器，从而能够找出正确的行和列索引
T r = { i ∣ ? j : ( i , j ) ∈ T } T c = { j ∣ ? i : ( i , j ) ∈ T } T_r=\{i|\exists j:(i,j)\in T\} \\ T_c=\{j|\exists i:(i,j)\in T\} Tr?={i∣?j:(i,j)∈T}Tc?={j∣?i:(i,j)∈T}

3. 表格序列化

? 可以简单的使用空格来连接行或者列的取值，从而实现表格的序列化。但是，最好能够将表格结构也合并至序列化的文本中。这里假设表格是单层表头，多层表头可以拉平后再应用该方法

? 行($S_i^r$)和列($S_j^c$)序列化表示形式化为
$$\begin{array}{r}{S}_i^r=\underset{j=1}{\overset{n}{?}}{\zeta }_h(h_j)\oplus {\zeta }_v(v_{i,j})\\ S_j^c={\zeta }_h(h_j)\oplus \underset{i=1}{\overset{m}{?}}{\zeta }_v(v_{i,j})\end{array}$$
其中，$\oplus$表示拼接，函数${\zeta }_h$和${\zeta }_v$用于分隔表头和单元格取值。对于${\zeta }_h$会在表头后增加符号“：”，对于${\zeta }_v$则会在单元格取值后添加符号“|”。

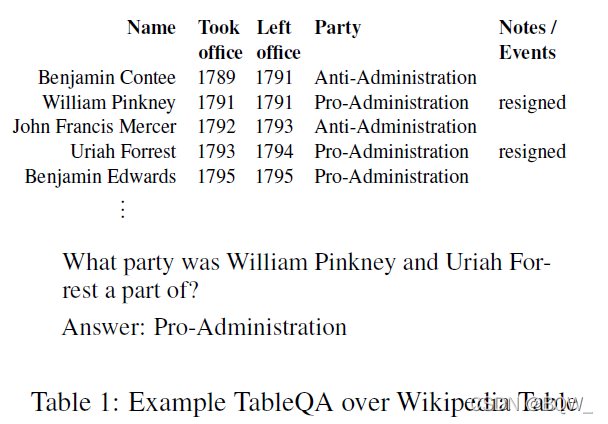
? 以上表为例，该表格的第一行被转换为
$$\text{Name:Benjamin?Contee|Took?office:1789|Left?office:1791|Party:Anti-Administration|Note/Events:|}$$
该表的第二列被转换为
$$\text{Took?office:1789|1791|1792|1793|1795|}$$
? 无论是$\text{Interaction}$版本或者$\text{Representation}$版本模型都会使用上面的序列化表示。

4. $\text{Interaction}$模型

? 在$\text{Interaction}$版本中，序列化文本会使用$\text{[CLS]}$和$\text{[SEP]}$与问题进行拼接。然后这个序列对被输入至$\text{ALBERT}$。最终$\text{[CLS]}$隐藏层的输出用于后面的线性层和$\text{softmax}$，判断行或者列是否包含答案。

5. $\text{Representation}$模型

? 上图是$\text{Representation}$版本模型的结构，问题$r_q$的向量表示和$j$列$r_c$的向量表示会先被分别算出来。然后，这两个向量按各种方式进行拼接，并使用带有$\text{softmax}$层的全连接层对拼接后的向量进行分类
$$\begin{array}{rl}{\text{r}}_{\delta }& ={\text{r}}_q?{\text{r}}_c\\ {\text{v}}_{qc}& ={\text{r}}_q:{\text{r}}_c:{\text{r}}_q?{\text{r}}_c:{\text{r}}_{\delta }?{\text{r}}_{\delta }\\ p(j\in T_c)& =softmax({\text{Wv}}_{qc}+\text{b}{)}_0\end{array}$$

6. 扩展至聚合类问题

? 虽然模型$\text{RCI}$主要聚焦在查询类问题，但也可以使用额外的问题分类器来实现对聚合类问题的回答。具体来说，使用另外一个transformer来对“问题-表头”对进行分类，类别为：$\text{lookup,max,min,count,sum,average}$。然后，设定一个阈值来选择一部分单元格，并使用具体的操作类型(平均、求和等)来对这些单元格进行操作。