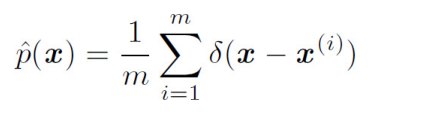伯努利分布(Bernoulli distribution)
**伯努利分布:**单个二值随机变量的分布。由单个参数φ∈[0,1]控制。
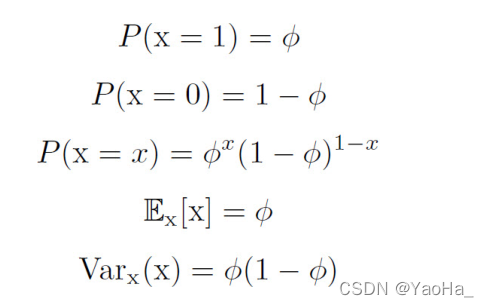
例:抛硬币,正面朝上的概率。
二项式分布(binomial distrubution)
二项式分布:在n次试验中事件A恰好发生k次的概率。
概率计算:
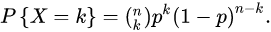
式中k=0,1,2,…,n,
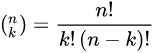
期望计算:E(x)=np
方差计算:D(x)=np(1-p)
例:抛n次硬币,正面朝上出现m次的概率。
多项式分布(multinoulli distribution)
多项式分布:具有k个不同状态的单个离散型随机变量上的分布,其中k是一个有限值。式二项式分布的扩展。
概率计算:
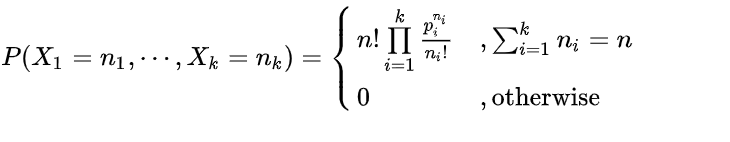
例:多次抛筛子,统计各个面被掷中的次数的概率。
高斯分布(Gaussian dis-tribution)
高斯分布(Gaussian dis-tribution),也称为正态分布 (normal distribution)。 即:
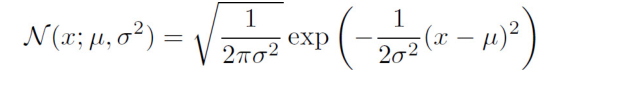
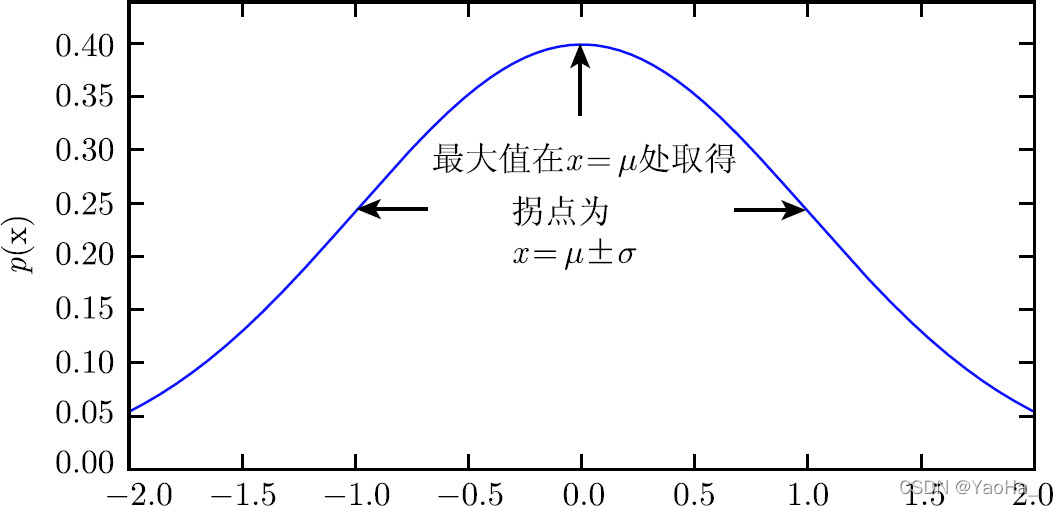
注:正态分布呈现经典的“钟形曲线”的形状,其中中心峰的x坐标由μ给出,峰的宽度受σ 控制。在这个示例中,我们展示的是标准正态分布(standard normaldistribution),其中μ=0,σ=1。
期望计算:E(x)=μ
方差计算:D(x)=σ^2
指数分布(exponential distribution)
指数分布(exponential distribution):在x=0点处取得边界点(sharp point)的分布。即:
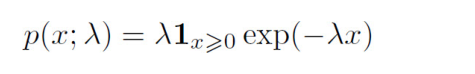
指示函数(indicator function):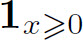
指数分布用指示函数来使得当x取负值时的概率为零。
拉普拉斯分布(Laplace distribution)
拉普拉斯分布(Laplace distribution):随机变量的概率密度函数分布。即:
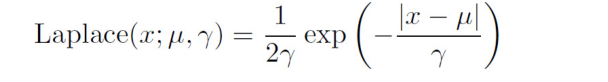
Dirac分布
Dirac delta函数(Dirac delta function):被定义成在除了0以外的所有点的值都为0,但是积分为1。
Dirac分布经常作为经验分布 (empirical distribution) 的一个组成部分出现: