开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> Neural Network Fundamentals (1) -> 正文阅读

[人工智能]Neural Network Fundamentals (1)

Reference:

Neural Network and Learning Machines: International Edition, 3/e (Author: Haykin, ISBN:9780131293762)
人脑是专用计算机，通过神经元中的链接对经验进行存储；而计算机属于通用计算机，通过设计逻辑算法实现程序。因此结构不同，导致了人脑能够轻易实现人脸识别，语音辨别等等不是通过纯逻辑实现的事，因此通用计算机为了能够达到与大脑类似的效果，需要对大脑模型进行模拟，从而实现类似的功能。

大脑的基本结构

大脑结构
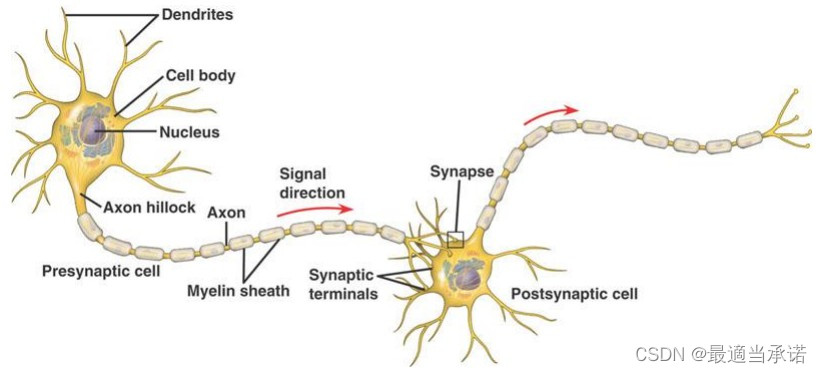
大脑由神经元组成，每个神经元由细胞本体，树突和轴突三部分所组成。不同神经元之间的信号由轴突输入神经元，经过细胞本体，然后通过树突然后传递到下一个细胞中。（化学信号-电信号-化学信号）

神经元网络的基本特征

一个神经元同时是多个神经元的受体，也可以将信号传递给多个其他的细胞。（另外细胞也并非单向传递）
神经元的信号是多个细胞信息输入的叠加（信息有正有负，也就是有激活也有抑制）（因为突触是有激励因子，也有抑制因子）
神经元的信号输入和输出并不呈现线性关系。首先存在一定的阈值，当信号超过一定的阈值之后就会快速上升。简单来看可以看作 sign 函数，输入之和超过一定阈值之后就会激活神经元。
神经元更高强度的兴奋不是有更高的输入造成的，而是由更高频率的有效刺激造成的。

通过大脑结构构建基本神经元模型

一个神经元有多个输入，然后有一个输出。
输入信号来自于不同的神经元，有不同的权重，可正可负（激励型和抑制型）。
神经元本身的输入可以简单看作两个结果：激励状态和未被激励状态。（0和1）
因此可以将神经元简单看作两个过程：
过程一： $v(\vec x) =\vec w^T \vec x + b$
其中， $\vec x = [x_1,x_2, \dots, x_n]^T, weights: \vec w =[ w_1,w_2, \dots, w_n], b: threshold }$
过程二： $\varphi(v)$
其中， $\varphi = sign}$ ，存在激活函数，当 ${ v>=0, y =1; v<0, y=0 }$

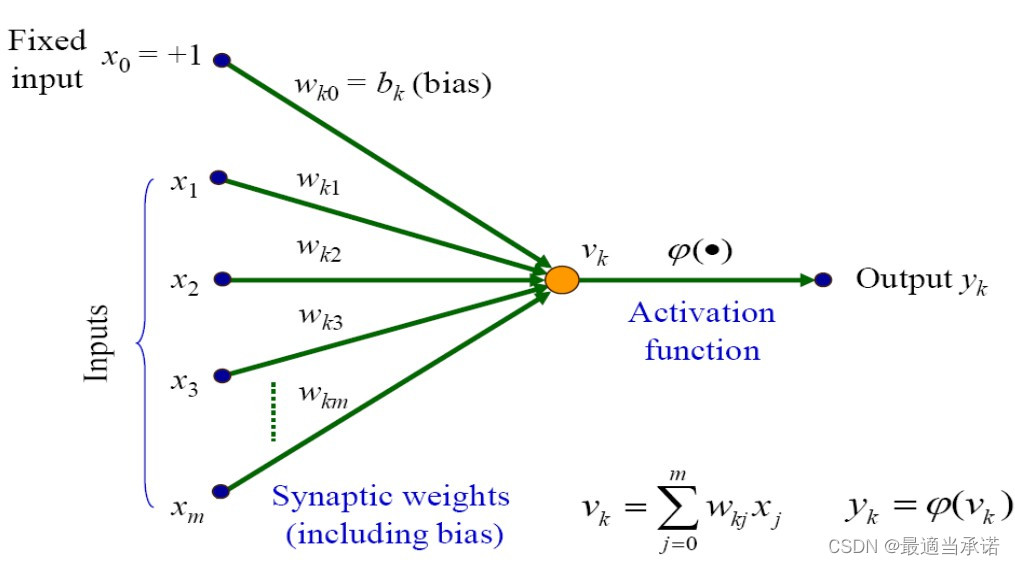
因此最终的函数可以表示为：
$\varphi( \vec w^T \vec x +b )$
因为阶跃函数不是连续函数，因此最终的函数也不是连续函数，而是单纯两个值的输出。
当我们将激活函数换成其他的函数，比如
sigmoid function: ${\varphi (v) = \frac{1}{1+e^{-av}}}$
tanh function： $\varphi(v) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}}$
连续并且可导，那么该神经元结果就是连续并且可导的。

Perceptron

一个神经元在初期被称为感受器perceptron，对感受器的理解是对神经元网路理解的基础。

二分类问题

因为感受器的输出为0和1，因此可以作为感受器，实现标签的分类。当 ${\vec w^T \vec x >=0}$ ，标签结果为一类；当 $\vec w^T \vec x <0 }$ ，标签结果为另外一类。因此我们可以看到感受器实际上是一个线性二分类器。通过创造出一条直线或者一个超平面，实现不同标签的分类。线性可分的问题(linearly separable)才能用感受器实现，而且只要是线性可分，感受器一定能够实现。

如何得到想要的权重

对于低维度的点来说，我们可以直接肉眼观察，然后得到边界线和权重。
对于高维度的分类问题，我们只能通过learning来实现。

问题定义

我们有m个点，对于每一个点 ${\vec x_i = [1, x_1,x_2, \dots, x_{n-1}]}$ ，然后有想要的标签 ${ d_i }$ 。
我们随机定义了权重 ${\vec w = [b,w_1,w_2, \dots, w_{n-1}]}$ 。
我们想要实现，对于每一个点，都能实现 $\varphi(\vec w^T \vec x_i) = d_i }$ .

问题分析

对于m个点，假设存在一组 ${\vec w}$ 能够实现所有点的正确划分。
对于 ${d_i = 1}$ 的点来说，如果划分错误，使得 ${\vec w^T \vec x <0}$ ，我们应该更新权重 ${\vec w_n = \vec w_{n-1} + \Delta \vec w}$ 。 $\Delta w$ 应该能使得 ${\vec w^t \vec x}$ 整体值变大。所以 $\Delta \vec w = \eta \vec x (\eta>0) }$
对于 ${d_i=0}$ 的点来说，如果划分错误，我们应该更新权重，使得结果朝着 $\vec w^T \vec x }$ 减小。所以 ${\Delta \vec w = - \eta x}$
我们定义误差error: $d_i - \vec w^T \vec x_i}$
那么我们将结果上述结果合起来: ${\Delta \vec w = \eta e \vec x}$
${\eta}$ 作为权重，能够改变每一步的更新速率。

算法

确定学习速率 ${\eta}$
随机生成权重 ${\vec w}$

for ${x_i, d_i}$ in all points
计算 $d_i - \vec w^T \vec x }$
然后更新权重： $w_n = w_{n-1} + \eta e \vec x }$

对于线性可分的问题，我们可以等到零误差（所有标签全都正确），再停止结果。对于线性不可分的问题，我们可以计算一定的循环次数，然后停止。

感受器必然能够实现线性可分问题的原因

Perceptron Convergence Theorem: (Rosenblatt, 1962)
此文章证明了感受器对于线性可分的问题必然会收敛。

回归问题

回归问题难以实现对于所有点的正确标记，因此我们通常将其视为优化问题，所有点的误差之和最少：
${E(\vec w) =\frac{1}{2} \sum_n^{i=1}e(i)^2 =\frac{1}{2} \sum^n_{i=1}[d(i)-y(i)]^2 }$

分析问题

首先我们定义几个相关变量：

$\vec d = [d_1,d_2, \dots,d_n]^T$
$X=[\vec x_1, \vec x_2, \dots, \vec x_n]$
$\vec e = \vec d - X^T \cdot \vec w$
$E(\vec w) =\frac{1}{2} \vec e^T \vec e$
其中 X 的维度是 (m,n)，其中 m是变量的维度， n是数据点的数量。
然后，我们为了得到最优解，我们必须求解cost function梯度为零的点：
$\begin{aligned} \bigtriangledown ( E(\vec w) ) &= 0 \\ \bigtriangledown_{\vec w} ( E(\vec w) ) &= \vec e^T \cdot (-X^T) \\ (\vec d^T - \vec w^T X) X^T &= 0 \\ \vec w^T X X^T &= \vec d X^T \\ X X^T \vec w &=X \vec d^T \\ \vec w &= (X X^T)^{-1}X \vec d^T \\ \end{aligned}$
其中 $X X^T)^{-1}$ 也就是 X的伪逆。该方程对于维度较低时较为有用，但是对于较多的数据时，对内存要求比较高。因此，对于较多的数据，可以使用以下的方式： learning。

Learning

我们将 $E(\vec w)$ 看作连续可微分的函数，那么我们每次更新 $\vec w$ 都朝着使得 $E(\vec w)$ 下降最快的方向变化，就能找到局部最优点。
因此，我们每次更新 $\vec w$ 的公式就是：
$\begin{aligned} \vec w_n &= \vec w_{n-1} - \eta \bigtriangledown_{\vec w}E(\vec w) \\ \vec w_n &= \vec w_{n-1} + \eta e(n) \vec x(n) \end{aligned}$
其中, $e(n)=d(n)-\vec w^T \vec x(n)$

Multi-layer Perceptron

由于单个感受器只能实现已一条直线的模拟，只能完成对于线性可分的问题的解答，或者对于线性关系尽心拟合，难以完成更加复杂的问题求解，甚至连XOR都难以模拟。因此，出现了多个神经元相连结的神经元网络。

XOR问题引入

对于XOR问题，单个感受器是无法进行模拟的。

input 1	input 2	output
$x_1$	$x_2$	$y$
0	0	0
1	0	1
0	1	1
1	1	0

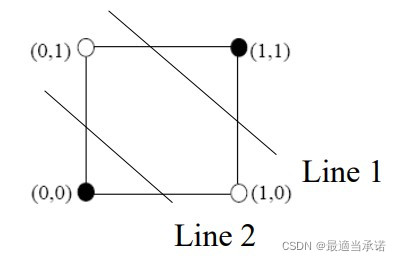
在这里插入图片描述
因为感受器只能生成一条边界线，无法生成两条。
如果我们使用两个输出,而不是单个输出：

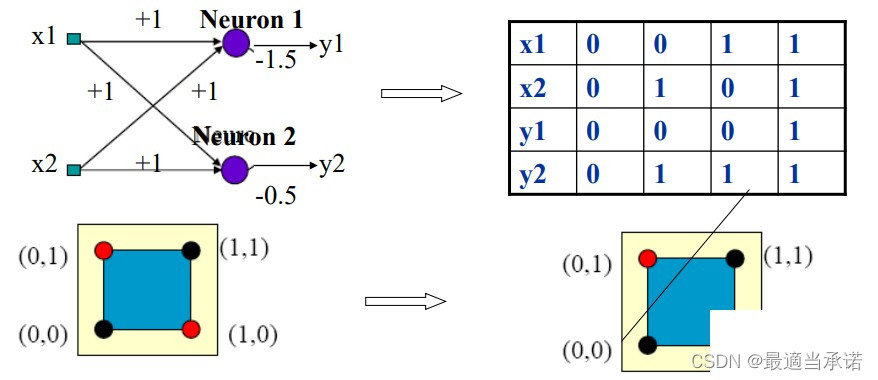
此时我们发现XOR问题中 (0,1) 和 (1,0 )变成了一个点，实现了空间位置的转变，变成了可以线性可分的问题。此时，将这两个输出作为输入，连接在一个感受器（神经元）上，就可以实现XOR问题的模拟。

多层神经网络

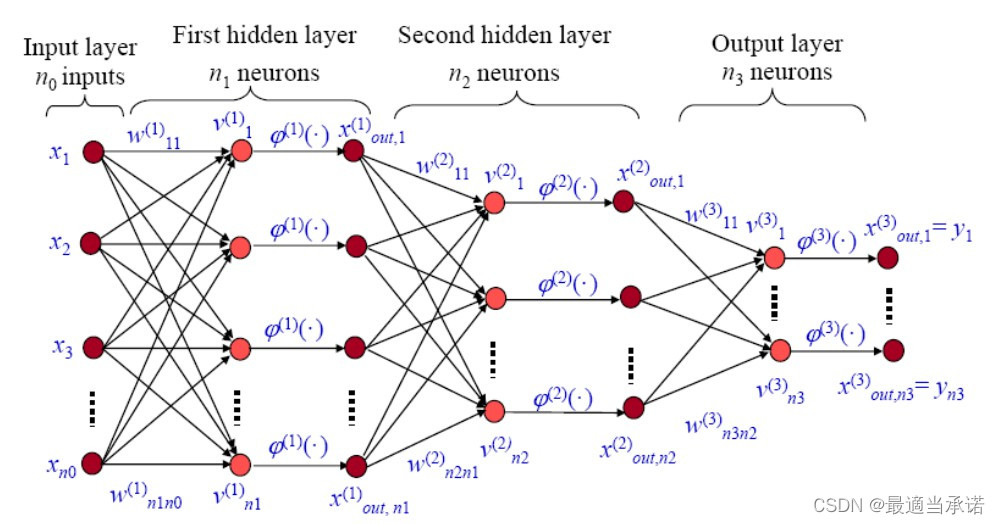
在这里插入图片描述
我们在考虑神经网络的层数时，不考虑输入层，只考虑隐藏层和输出层。一个全连接层和一个激活层组成了一个神经网络层。对于每一层的全连接层，都是 $\vec w \vec x+b$ 。对于激活层，我们则可以根据我们的需要进行修改，比如RELU，sigmoid function, atanh函数等等。

LMS 方法

我们仍然将其看成一个优化问题：
需要解决的问题：我们目前神经网络中的权重都是随机生成的，我们需要通过输出结果和我们的label( d )之间的误差e，对权重进行更新，减小生成的误差。
对于每一个数据点所产生的误差：
$\frac{1}{2}\sum_{j=1}^{n_3} e_j(i)^2=\frac{1}{2}\sum_{j=1}^{n_3}[d_j(i)- x_{out,j}^{(3)}(i)]^2$
对于同时对一批数据点进行处理：
$=\frac{1}{2} \sum_{i}^{m} \sum_{j=1}^{n_3} e_j(i)^2$
我们对每个点进行分别处理，而不采取批处理，因为批处理容易陷入局部最优；对数据进行分别处理，则有助于增加noise，能够跳出局部最优，因此对每个点单独进行处理则比较好。
我们再使用梯度下降法：
$\Delta w_{ji}^{(s)}(n) = - \eta [ \frac{\partial E(n)}{\partial w_{ji}^{(s)}(n)}]^T$
其中，s对应第一，二，三层；j是i的下一层。

Back Propagation

第三层权重更新

$\begin{aligned} v^{(3)}_j &=\sum_i^{n_2}w^{(3)}_{ji} x_{out,i}^{(2)} \\ x_{out,j}^{(3)} &=\varphi^{(3)}[ v_{j}^{(3)} ] \\ error: e_j(n) &= d_j(n)-x_{out,j}^{(3)} \end{aligned}$
我们根据链式法则，可以对第三层权重进行更新：
$\begin{aligned} \frac{\partial E}{\partial w^{(3)}_{ji}} &= \frac{\partial E}{\partial e_j(n)} \frac{\partial e_j(n)}{\partial x^{(3)}_{out,j}} \frac{\partial x^{(3)}_{out,j}}{\partial v_j^{(3)}}\frac{\partial v_j^{3()}}{\partial w^{(3)}_{ji}} \\ &=e_j(n) \cdot (-1)\cdot \varphi^{(3)'}[v_j^{(3)}] \cdot x^{(2)}_{out,i} \\ &= -e_j(n)\varphi^{(3)'}[v^{(3)}_j]x^{(2)}_{out,i} \end{aligned}$
另外，我们可以定义 $\delta^{(3)}_j(n)=e_j(n)\varphi^{(3)'}[v_j^{(3)}]$ ，则上式可以写成
$\frac{\partial E}{\partial w^{(3)}_{ji}}=-\delta_j^{(3)}(n)x^{(2)}_{out,i}(n)$
因此我们可以得到第三层权重的更新公式：
$w_{ji}^{(3)}(n+1) = w_{ji}^{(3)}(n)+ \eta \delta_j^{(3)}(n)x_{out,i}^{(2)}(n)$
其中 $\delta_j^{(3)}$ 可以看作输出误差， $x_{out,i}^{(2)}(n)$ 可以看作输入信号。

第二层权重更新

在这里插入图片描述
我们采用和上述同样的方式，采用链式法则求解。
$\begin{aligned} \frac{\partial E}{\partial w_{j,k}^{(2)}} &=\frac{\partial E}{\partial x^{(3)}_{out,i}} \frac{\partial x^{(3)}_{out,i}}{ \partial v_i^{(3)}} \frac{ \partial v_i^{(3)}}{\partial x_{out,j}^{(2)}}\frac{ \partial x_{out,j}^{(2)} }{ \partial v_{j}^{(2)} } \frac{\partial v_{j}^{(2)}}{\partial w_{j,k}^{(2)} } \\ &=-e_{i}(n) \varphi^{(3)'}[ v_i^{(3)} ]w^{(2)}_{i,j} \varphi^{(2)'}[ v_j^{(2)}] x^{(1)}_{out,k} \\ &= -\delta_i^{(3)}w^{(2)}_{i,j}\varphi^{(2)'}[v_j^{(2)}]x_{out,k}^{(1)} \end{aligned}$
但是我们可以看到上式的i是一个不定量，因为我们在对 $w_{j,k}^{(2)}$ 进行求导的时候，我们没有包含i的信息。而且 $w_{j,k}^{(2)}$ 对于第三层中的所有输出都会有影响，因此实际上这里的链式法则应该对i进行求和！
$\begin{aligned} \frac{\partial E}{\partial w_{j,k}^{(2)}} =- \sum_i^{n_3} [ \delta_i^{(3)}w^{(3)}_{i,j}]\varphi^{(2)'}[v_j^{(2)}]x_{out,k}^{(1)} \end{aligned}$
此时，我们定义一个变量： $\delta_j^{(2)}=\sum_i^{n_3} [ \delta_i^{(3)}w^{(3)}_{i,j}]\varphi^{(2)'}[v_j^{(2)}]$
那么第二层的权重可以写作：
$\Delta w_{j,k}^{(2)} = - \delta_{j}^{(2)}x_{out,k}^{(1)}$

第一层权重

同样的形式，我们可以写成：
$\begin{aligned} \delta_k^{(1)} &=\sum_j^{n_2}[\delta^{(2)}_j w^{(2)}_{jk}] \varphi^{(1)'}[v^{(1)}_k]\\ \Delta w^{(1)}_{k,l} &= -\delta_k^{(1)}x_{l} \\ \end{aligned}$

Back Propagation

我们可以看到，对于每一个数据点 $[x_1(n), x_2(n), \dots, x_m(n)]^T$ ，我们可以正向传递得到最后的结果，然后根据正向得到的 $\delta_i^{(3)}$ 反向去求解 $\delta_j^{(2)}$ ，根据 $\delta_j^{(2)}$ 求解之前的 $\delta_k^{(1)}$ ,根据不同层的 $\delta$ 对不同层的权重进行更新。
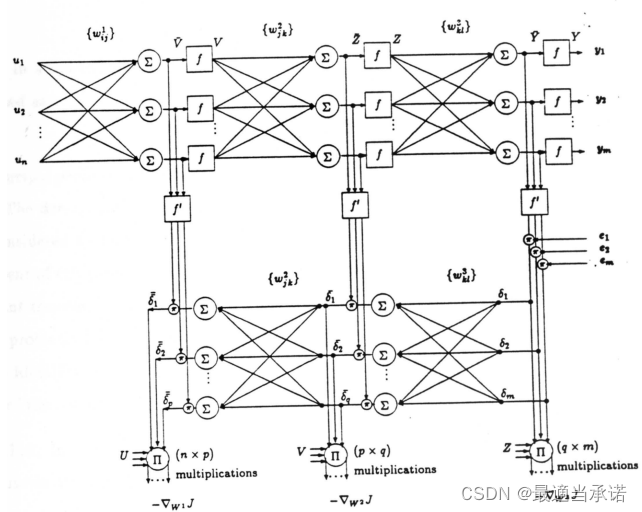
在这里插入图片描述

真正的权重更新

$\begin{aligned} \Delta w_{ji}^{(s)}(k) &= \alpha \Delta w_{ji}^{(s)}(k-1)+ \eta^{(s)}\delta_j^{(s)}(k)x^{(s-1)}_{out,i}(k) \\ &= \alpha^2 \Delta w_{ji}^{(s)}(k-2) + \eta^{(s)}[ \alpha \delta_j^{(s)}(k-1)x^{(s-1)}_{out,i}(k-1) +\delta_j^{(s)}(k)x^{(s-1)}_{out,i}(k) ] \\ &=\eta^{(s)}\sum_{t=0}^{k} \alpha^{k-t}\delta_j^{(s)}(t) x_{out,i}^{(s-1)}(t) \end{aligned}$
这样每次权重的更新都是之前所有误差项的加权平均。越往后的误差项，权重越高。这样的更新相当于增加了惯性项。同时权重的更新并不只是一个点数据的影响，而是之前所有点数据的影响：这样的梯度方向相当于能够使得之前所有的点误差减小，因此能够使得结果更加的稳定。